The series of overtones

As we know, the octave is the first overtone. The physical phenomenon of resonance has helped us understand the role played by the overtones: in the physical world, vibrating media such as strings or pipes can vibrate with their basic frequency, but also with an integral multiple of this frequency. In this way the octave results as the first integral multiple of the basic frequency – i.e. by the fact that its frequency is doubled.

It would now be obvious to add the further overtones, which are also integral multiples of the basic frequency, and to explain the single notes of the musical scales in this way.

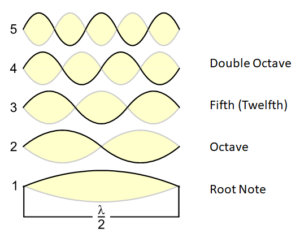
Fig. 1: The fundamental tone and the first four harmonics

Fig. 1 shows how a string vibrates and how the octave and further overtones are added. Whereas the fundamental tone vibrates with precisely one “belly”, the overtones vibrate with two, three, four and more bellies. If we start with the fundamental tone C, this will result in the following series of overtones:

Fig. 2: Overtone series ranging from the fundamental tone C (note 1) to c“‘ (note 16)

The musical scale works in a closed frequency range

Resonance explains the overtone series, including the octave. How, though, does a musical scale come about, which is meant to fill the narrow range between the fundamental tone and the first overtone, i.e. the octave? As mentioned in the previous post, the notes of the musical scales are subject to this constraint whereby they all have to be within the range of an octave. The overtone series, however, leads far beyond an octave.

In addition, Fig 2 also reveals that the distances between the overtones vary a great deal. Whereas initially, they are very far apart, they get closer and closer as the series proceeds. This would be highly impractical for a musical scale to be applied in reality.

We see, however, that the overtones from note 4 onwards, and even more between notes 8 and 16, constitute something like a kind of major scale: c, d, e, (f), g (a), (h), h, c: nearly our major scale, but not exactly, since the tones in brackets (11, 13, 14) don’t quite fit.

The natural “musical scale” of the alphorn

In fact, the musical scale between notes 8 and 16 corresponds to the natural musical scale of the alphorn – including, however, the “off” notes 11, 13 and 14, and without the actually important fourth, namely the f. Nonetheless, the natural tone series of the alphorn – but also only between notes 8 and 16 – is almost something like a natural musical scale in that it packs a reasonable number of notes into the range of an octave, and this even on the basis of resonance.

Yet the overtone series that can be played on the alphorn is still not a real musical scale. Only the musical scale between notes 8 and 16 can be played on this instrument; most notes of the musical scale below this range are missing while above it, there is a confusing array of many more tones, which are increasingly closer to each other. This is not tantamount to a musical scale which repeats itself octave after octave. Additionally, the instrument is somewhat impractical. In order for the notes to be played at a normal pitch, the horn must of necessity be very long. This is different with a violin or a flute, i.e. substantially more practical. With these smaller instruments, however, we cannot achieve the tones of the musical scale as overtones (which would be flageolet tones with the violin, and with the flute pure overblows like with the alphorn), but by means of deliberate mechanical manipulation of the physical object that vibrates, namely the strings of the violin and the air column of the flute.

But do the overtones and resonances play a role in the musical scales nonetheless? – They do! You can read about this in the next post, which explains how a fifth comes about.

This is a post about the theory of the three worlds.