Starting point: two gaps
In the previous post, we saw that in the sequence of the ten scales tones found so far, there are two gaps. Can we find resonant tones there, too? We already know the following:
- We already know the ten most resonant intervals in the octave.
- These ten intervals serve to constitute the five standard pentatonic scales and our major and minor scales. There, the gaps are not obtrusive; they are only conspicuous in the distribution of all the ten potential scale tones.
- Intervals do not occur on their own, either in a chord or in a melody. Thus if we have a resonant interval, we add another one to it and calculate the resulting sum interval. Or we look at the distance between two intervals and calculate the distance between both intervals, i.e. we subtract one from the other.
- Owing to the exponential progression of the frequencies, and contrary to our intuitive expectation, when we calculate the frequency of the two intervals added together, we do not have to build the sum of the two interval fractions, but have to multiply them, and with regard to the distance between the two intervals, we must not subtract one interval from the other, but divide one by the other.
Since we have already found all the resonant intervals within the octave, we cannot expect any more highly resonant intervals for the two gaps. Yet although, if we are successful, the intervals are not all that resonant any longer in terms of their resonance with the fundamental tone, they may still have direct and thus very resonant relations to other scale tones. In musical configurations, this also makes them interesting in terms of resonance, depending on the situation.
Here are my attempts to fill in tones for the gaps. To illustrate this, I will first show the distribution of the ten most resonant intervals from the previous post:
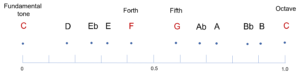
Fig. 1: Distribution of the ten most resonant scale tones in an octave (logarithmic representation)
The minor seconds
Regarding the first gap, we cannot find a tone with good resonance with the fundamental tone. Because the two tones of the interval must be close together, the fraction of their frequencies must be close to 1 and therefore its numerator and denominator cannot be small numbers – as would be preferred for a good resonance. We therefore check as candidates fractions that are still created by relatively small numerators and denominators:
Octave – major seventh = 2 : 15/8 = 16/15 = 1.067
Fourth – major third = 4/3 : 5/4 = 16/15 = 1.067
Minor sixth – fifth = 8/5 : 3/2 = 16/15 = 1.067
Minor third – major second = 6/5 : 9/8 = 48/45 = 16/15 = 1.067
Major third – minor third = 5/4 : 6/5 = 25/24 = 1.042
Major seventh – minor seventh = 15/8 : 9/5 = 75/72 = 25/24 = 1.042
Major sixth – minor sixth = 5/3 : 8/5 = 25/24 = 1.042
Minor seventh – major sixth = 9/5 : 5/3 = 27/25 = 1.08
In this way, we can find several intervals which satisfy the requirements and fit into the first gap:
- 16/15 = 1.042
– major third – minor third
– major sixth – minor sixth
– major seventh – minor seventh - 25/24 = 1.067
– minor third – major second
– minor sixth – fifth
– fourth – major third
– octave – major seventh - 27/25 = 1.08
– minor seventh – major sixth
These three intervals all sound rather twangy. We call them minor seconds. In the pure temperament, there are at least three of them.
The tritones
The second gap is right in the middle of the musical scale. We are now going to try to fill this gap with a combination of two known resonant intervals:
Major seventh – fourth = 15/8 : 4/3 = 45/32 = 1.406
Minor seventh – major third = 9/5 : 5/4 = 36/25 = 1.44
Major sixth – minor third = 5/3 : 6/5 = 25/18 = 1.389
Octave + minor third – major sixth = 2 x 6/5 : 5/3 = 12/5 : 5/3 = 36/25 = 1.44
Once more, this results in three intervals that are close together:
- 25/18 = 1.389
- 45/32 = 1.406
- 36/25 = 1.440
Insertion of the minor seconds and the tritones into the sequence of the scale tones
Our calculations so far have concerned frequency ratios. As explained in the previous post, we have to convert them logarithmically to ensure that their distances correspond to what we perceive in our mental world. In a logarithmic representation (on basis 2), we arrive at the following distribution:
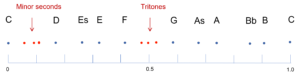
Fig. 2: The three minor seconds (“semitones”) and three tritons fill the gaps of Fig. 1
Although we can see that the proposals fill their respective gaps well, we have three proposals for each gap! Which of them is the best? We could argue in favour of that with the smallest figures in the numerator and denominator, or in favour of that with the greatest frequencies among the variants, or in favour of that with the closest relation to a musical scale we already know. However, it is for a good reason that we defer this issue until we deal with the well-tempered scales.
This is a post about the theory of the three worlds.