Objects and relations
Let us first take a set of objects and consider how many connections (relations) there are between them, leaving aside the nature of the relationships and focussing solely upon their number. This is quite a simple task, because there is always exactly one relation between any two objects. Even if the two objects are entirely unrelated, this fact has a meaning and is thus useful information. We can count the number of possible connections between the objects and compare the number of objects with the number of possible relations.
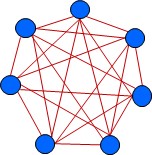
Fig 1: Seven objects and their relations
Figure 1 shows seven objects (blue) and their relations (red). Every object is connected to every other object. Thus, in our example, each of the 7 objects is connected to 7-1 = 6 other objects, giving a total of 7 * 6 / 2 = 21 relations. The general mathematical formula for this is NR = (NO2 – NO) / 2, where NR is the number of relations and NO is the number of objects.
As we can see from the formula, the number of relations increases in proportion to the square of the number of objects. Or, to put it non-mathematically:
There are always a great many more relations than there are objects!
Below is a small table showing the number of relations for a given number of objects:
NO NR
———————-
1 0
2 1
3 3
4 6
5 10
6 15
7 21
8 28
9 36
10 45
100 4,950
1000 499,500
Table 1: Objects and relations
While the numbers in the first column are small, the quadratic increase is not particularly noticeable. However, as these numbers rise it quickly becomes more marked. Before we turn our attention to the practical implications of this, let us first take a look at the number of possible combinations.
Objects and combinations
The term ‘combination’ refers to the ways in which a number of objects can be combined with each other. Whereas a relation always relates to precisely two objects, combinations can include any number of objects from 1 to all (= NO).
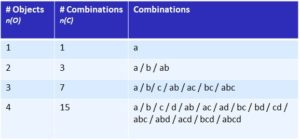
Table 2: Objects and combinations
Table 2 shows objects and the number of combinations between them for 1 to 4 objects, with the number of objects in the first column and the number of combinations in the second. The objects are identified by letters (a, b, c ,d) and the possible combinations are shown in the column on the far right. When there is only one object (a) there is just one combination consisting solely of this element; when there are 2 the number of combinations rises to 3 and when there are 4 it is 15. The number of combinations per object therefore increases even faster than the number of relations (as described above). The formula for this is: NC = 2No – 1.
As we saw earlier, the relationship between objects and their relations is quadratic. The relationship between objects and combinations, on the other hand, is based upon exponential growth, meaning that it rises even more quickly. When there are 10 objects, the number of combinations is 1023; when there are 100, this figure rises to an incredible 1,267,650,600,600,228,229,429,401,496,703,205,375 or 1.26 * 1036 !
The number of combinations thus increases extremely rapidly.
This exponential increase forms the basis for the combinatorial explosion.
Combinatorial explosion
Let’s suppose we have a number of different objects with different properties, for example:
4 shapes: round, square, triangular, star-shaped.
8 colours: red, orange, yellow, green, blue, brown, white, black.
7 materials: wood, PVC, aluminium, cardboard, paper, glass, stone.
3 sizes: small, medium-sized, large.
We can now combine these four classes and their 22 properties in any way we want. For example, an object may be triangular, green, medium-sized and made of PVC. Based upon these 22 properties, how many different types of objects can we distinguish between?
We can select one property independently from each of the four classes (shape, colour, material, size), giving a total of 4x8x7x3 = 672 possible combinations. This means that, if there are 22 properties, we can describe 672 different objects. For every additional class, the number of possibilities is multiplied.
It doesn’t take many additional classes before the number of possible combinations explodes.
This is the combinatorial explosion. And it plays a critical role in any information processing – especially when the information relates to the real world, where the number of classes has no natural limit.