continues paradoxes and logic (part 2)
History
Before we Georg Spencer-Brown’s (GSB’s) distinction as basic element for logic, physics, biology and philosophy, it is helpful to compare it with another, much better-known basic form, namely the bit. This allows us to better understand the nature of GSB’s distinction and the revolutionary nature of his innovation.
Bits and GSB forms can both be regarded as basic building blocks for information processing. Software structures are technically based on bits, but the forms of GSB (‘draw a distinction’) are just as simple, fundamental and astonishingly similar. Nevertheless, there are characteristic differences.
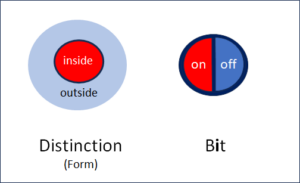
Fig. 1: Form and bit show similarities and differences
Both the bit and the Spencer-Brown form were found in the early phase of computer science, so they are relatively new ideas. The bit was described by C. A. Shannon in 1948, the distinction by Georg Spencer-Brown (GSB) in his book ‘Laws of Form’ in 1969, only about 20 years later. 1969 fell in the heyday of the hippie movement and GSB was warmly welcomed Esalen, an intellectual hotspot and starting point of this movement. This may have put him – on the other hand – in a bad light and hindered the established scientific community to look closer into his ideas. While the handy bit vivified California’s nascent high-tech information movement, Spencer-Brown’s mathematical and logical revolution was rather ignored by the scientific community. It’s time to overcome this disparity.
Similarities between Distinction and Bit
Both the form and the bit refer to information. Both are elementary abstractions and can therefore be seen as basic building blocks of information.
This similarity reveals itself in the fact that both denote a single action step – albeit a different one – and both assign a maximally reduced number of results to this action, exactly two.
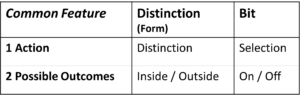
Table 1: Both Bit and Distinction each contain
one action and two possible results (outcomes)
Exactly one Action, Exactly Two Potential Results
The action of the distinction is – as name says – the distinction, and the action of the bit is the selection. Both actions can be seen as information actions and are as such fundamental, i.e. not further reducible. The bit does not contain further bits, the distinction does not contain further distinctions. Of course, there are other bits in the vicinity of the bit and other distinctions in the vicinity of a distinction. However, both actions are to be seen as fundamental information actions. Their fundamentality is emphasised by the smallest possible number of results, namely two. The number of results cannot be smaller, because a distinction of 1 is not a distinction and a selection of 1 is not a selection. Both are only possible if there are two potential results.
Both distinction and bit are thus indivisible acts of information of radical, non-increasable simplicity.
Nevertheless, they are not the same and are not interchangeable. They complement each other.
While the bit has seen a technical boom since 1948, its prerequisite, the distinction, has remained unmentioned in the background. It is all the more worthwhile to bring it to the foreground today and shed new light on what links mathematics, logic, the natural sciences and the humanities.
Differences
Information Content and Shannons Bit
Both form and bit refer to information. In physics, the quantitative content of information is referred to as entropy.
At first glance, the information content when a bit is set or a distinction is made appears to be the same in both cases, namely the information that distinguishes between two states. This is clearly the case with a bit. As Shannon has shown, its information content is log2(2) = 1. Shannon called this dimensionless value 1 bit. The bit therefore contains – not surprisingly – the information of one bit, as defined by Shannon.
The Bit and its Entropy
The bit measures nothing other than entropy. The term entropy originally came from thermodynamics and was used to calculate the behaviour of heat machines. Entropy is in thermodynamics the partner term of energy, but it applies – like the term energy – to all fields of physics, not just to thermodynamics.
What is Entropy ?
Entropy is a measure for the information content. If I do not know something and then discover it, information flows. In a bit, there are – before I know which one is true – two states possible, the two states of the bit . When I find out which of the two states is true, I receive a small basic portion of information with the quantitative value of 1 bit.
One bit decides about two results. If more than two states are possible, the number of bits increases logarithmically with the number of possible states; so it takes three binary elections (bits) to find the correct choice out of 8 possibilities. The number of choices (bits) behaves logarithmically to the number of possible choices, as the example shows.
Dual choice = 1 Bit = log2(2).
Quadruple choice= 2 Bit = log2(4)
Octuple choice = 3 Bit = log2(8)
The information content of a single bit is always the information content of a single binary choice, i.e. log2(2) = 1.
The bit as a physical quantity is dimensionless, i.e. a pure number. This suits because the information about the choice is neutral, and not a length, a weight, an energy or a temperature. The bit serves well as the technical unit of quantitative information content. What is different with the other basic unit of information, the form of Spencer-Brown?
The Information Content of the Form
The information content of the bit is exactly 1 if the two outcomes of the selection have exactly the same probability. As soon as one of the two states is less probable, its choice reveals more information. When it is selected despite its lower prior probability, this makes more of a difference and reveals more information to us. The less probable its choice is, the greater the information will be, if it is selected. The classic bit is a special case in this regard: the probability of its two states is equal by definition and the information content of the choice is exactely 1.
This is entirely different with Spencer-Brown’s form of distinction. The decisive factor lies in the ‘unmarked space’. The distinction distinguishes something from the rest and marks it. The rest, i.e. everything else, remains unmarked. Spencer-Brown calls it the ‘unmarked space’.
We can and must now assume that the remainder, the unmarked, is much greater, and the probability of its occurrence is much higher than the probability that the marked will occur. The information content of the mark, i.e. of the drawing the distinction, is therefore usually greater than 1.
Of course, the distinction is about the marked and the marked is what interests us. That is why the information content of the distinction is calculated based on the marked and not the unmarked.
How large is the space of the unmarked? We would do well to assume that it is infinite. I can never know what I don’t know.
The difference in information content, measured as entropy, is the first difference we can see between bit and distinction. The information content of the bit, i.e. its entropy, is exactly 1. In the case of distiction, it depends on how large the unmarked space is, but it is always larger than the marked space and the entropy of the distinction is therefore always greater than 1.
Closeness and Openness
Fig. 1 above shows the most important difference between distinction and bit, namely their external boundaries. These are clearly defined in the case of the bit.
The meaning in the bit
The bit contains two states, one of which is activated, the other not. Apart from these two states, nothing can be seen in the bit and all other information is outside the bit. Not even the meanings of the two states are defined. They can mean 0 and 1, true and false, positive and negative or any other pair that is mutually exclusive. The bit itself does not contain these meanings, only the information as to which of the two predefined states was selected. The meaning of the two states is regulated outside the bit and assigned from outside. This neutrality of the bit is its strength. It can take on any meaning and can therefore be used anywhere where information is technically processed.
The meaning in the distinction
The situation is completely different with distinction. Here the meaning is marked. To do this, the inside of the distinction is distinguished from the outside. The outside, however, is open and there is nothing that does not belong to it. The ‘unmarked space’, in principle, is infinite. A boundary is defined, but it is the distinction itself. That is why the distinction cannot really separate itself from the outside, unlike the bit. In other words: The bit is closed, the distinction is not.
Differences between Distinction and Bit
There are two essential differences between distionction and bit.
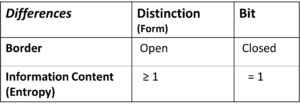
Table 2: Differences between Distinction (Form) and Bit
Consequences
The two difference between distinction and bit have some interesting consequences.
Example NLP (Natural Language Processing)
The bit, due to its defined and simple entropy and its close borders, has the technological advantage of simple usability, which we exploit in the software industry. Distinctions, on the other hand, are more realistic due to their openness. For our specific task of interpreting medical texts, we therefore came across the need to introduce openness into the bit world of technical software through certain principles: The keywords here are
- Introduction of an acting subject that evaluates the input according to its own internal rules,
- Working with changing ontologies and classifications,
- Turning away from the classical, i.e. static and montonic logic and turning towards a non-monotonic logic,
- Integration of time as a logical element (not just as a variable).
Translation: Juan Utzinger