Tag Archives: musical scales

Theory of the Three Worlds

The Perception of the Octave in the Mental World

Leave a comment

This is a post about the theory of the three worlds and continues the post about the resonance of the octave.

The subjective side

The mathematical world (Pythagoras) with its simple ratios and the physical world with its resonance phenomena provide us with an understanding of the octave but still fail to explain why this interval is the basis of all musical scales in all cultures. To understand this, we will also have to look at the mental world, i.e. the world of our subjective perception.

This world is accessible to everyone, but it will always remain your own and subjective perception. I can’t read your mind. Although imaging techniques such as MRI or PET are capable of observing which areas of the brain are active at what time, what they thus make perceptible is the flow of blood in a specific place, not the thought of how you experience it.

Happy Birthday

The mental world is your very personal world, but it makes quite a contribution to the primacy of the octave. Again, I propose a little experiment, not an objective one as in the preceding post, but still one that is verifiable. It has the advantage that in all likelihood, you will already have conducted it several times.

It can also be a Christmas carol in a family setting. Several people sing together, and if we are lucky, we sing with one voice. At any rate, this is usually our intention. It works better if all the singers have roughly the same register. But what if women and men and children sing together? We still recognise it if they all sing in unison. Although we do not sing in the same frequencies, but with frequencies that are an octave distant from each other, we practically don’t notice it. We perceive the distance of an octave as the same tone. If I, as a bass singing beside an alto, fail to hit the lower octave, I’m out of tune; if I do hit it, I sing in tune. This is the subjective effect of the octave: it is the same note.

The resonance in the physical world facilitates this subjective concurrence of the tones that are an octave distant from each other, and the resonance ratios on the basilar membrane of the inner ear support us in subjectively bringing the two frequencies together in our mental world, too.

First and second overtone

The octave is the first mathematically and physically possible overtone and in this respect it differs from the second overtone, which in the musical scale coincides with a fifth. To illustrate this mathematical correlation, I will again show the vibration ratios of the fundamental tone and the first overtones:

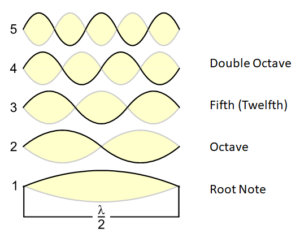
Fig. 1: Octave and fifth as overtones

Why, though, is the octave the characteristic of monophony rather than the fifth, although both of them are most closely related to the fundamental tone in mathematical and physical terms? Although mathematically the fifth is slightly farther distant from the fundamental tone than the octave, the double octave is still farther away, and yet we mentally perceive the double octave as the “same” tone as the fundamental tone, precisely like the octave.

In the mental world, i.e. in what we experience, there is a clear difference between the octave and the fifth. In this world, the octave (and all the multiple octaves) are the “same” tone, whereas the fifth is another tone. This applies all over the world, in all cultures. Since a tone which is an octave higher is perceived as the same tone, the musical scales repeat themselves an octave higher, but not a fifth.

An experiment to distinguish the octave from the fifth in the mental world

The Happy Birthday experiment described above can be extended to demonstrate the difference between the fifth and the octave, as well as the special role of the fifth. At the next birthday party, singers may try, for example, to sing the song not an octave, but a fifth lower (or higher). This is likely to be very difficult for you, precisely because you don’t sing the “same” notes as the others. And if you succeed, the others will look at you in amazement, precisely because you sing the fifth and “not the same tone”. The octave is the same tone, the fifth isn’t.

About access to the mental world

As is well known, the mental world is difficult to prove since it is completely subjective. Although all of us permanently live in this world with our thoughts and feelings, it is only indirectly accessible to objective scientific exploration. You can communicate the contents of your mental experience to other people, but you can never be quite sure that others will experience them in the same way. You can only hope that others will be able to understand your experience. Yet precisely this subjective experience and its comprehension make music so interesting: we share our subjectivity in a very specific way.

Conclusion

We can see how the mathematical, physical and mental worlds precisely meet in the octave. The uniform significance of the octave in all the world’s musical cultures can only be understood when we include all three worlds.

The next post will be about the other notes of the musical scales. Can they also be explained as simply as the octave?

This is a post about the theory of the three worlds.

Uncategorised

What Can I Know?

2 Comments

This website is powered by the question of how thinking works.

Information and Interpretation

How is data assigned a meaning? What does information consist of? The answer seems clear, as the bit is generally regarded as its building block.

Entropy is the quantity by which information appears in physics – thanks to C. E. Shannon, the inventor of the bit. Bits measure entropy and are regarded as the measure of information. But what is entropy and what does it really have to do with information?

Artificial Intelligence (AI)

Today there is a lot of talk about AI. I have been creating such systems for forty years – but without labelling them with this publicity term.

  • The big difference: corpus-based and rule-based AI
  • How real is the probable?
  • Which requires more intelligence: jassen (a popular Swiss card game) or chess?
  • What distinguishes biological intelligence from machine intelligence?

What today is called AI are always neural networks. What is behind this technology? Neural networks are extremely successful – but are they intelligent?

-> Can machines be intelligent? 

Logic

Mathematical logic, to many, appears to be the ultimate in rationality and logic. I share the respect for the extraordinary achievements of the giants on whose shoulders we stand. However, we can also think beyond this:

  • Are statements always either true or false?
  • Can classical logic with its monotonicity really be used in practice?
  • How can time be incorporated into logic?
  • Can we approach logical contradictions in a logically correct way?

Aristotle’s classical syllogisms still influence our view of the world today. This is because they gave rise to the ‘first order logic’ of mathematics, which is generally regarded as THE classical logic. Is there a formal way out of this restrictive and static logic, which has a lot to do with our static view of the world?

-> Logic: From statics to dynamics

Semantics and NLP (Natural Language Processing)

Our natural language is simply ingenious and helps us to communicate abstract ideas. Without language, humanity’s success on our planet would not have been possible.

  • No wonder, then, that the science that seeks to explain this key to human success is considered particularly worthwhile. In the past, researchers believed that by analysing language and its grammar they could formally grasp the thoughts conveyed by it, which is still taught in some linguistics departments today. In practice, however, the technology ‘Large Language Model’ (LLM) of Google’s has shattered this claim.

As a third option, I argue in favour of a genuinely semantic approach that avoids the gaps in both the grammar and the LLMs. We will deal with the following:

  • Word and meaning
  • Semantic architectures
  • Concept molecules

-> Semantics and Natural Language Processing (NLP)

Scales: Music and Maths

A completely different topic, which also has to do with information and the order in nature, is the theory of harmony. Rock and hits are based on a simple theory of harmony, jazz and classical music on complex ones. But why do these information systems work? Not only can these questions be answered today, the answers also provide clues to the interplay between the forces of nature.

  • Why do all scales span an octave?
  • The overtone series is not a scale!
  • Standing waves and resonance
  • Prime numbers and scales

-> How musical scales evolved

The author

My name is Hans Rudolf Straub. Information about my person can be found here.

Books

On the topics of computational linguistics, philosophy of information, NLP and concept molecules:

The Interpretive System, H.R. Straub, ZIM-Verlag, 2020 (English version)
– More about the book

Das interpretierende System, H.R. Straub, ZIM-Verlag, 2001 (German version)
– More about the book

On the subject of artificial intelligence:

Wie die künstliche Intelligenz zur Intelligenz kommt, H.R. Straub, ZIM-Verlag, 2021 (Only available in German)
– More about the book
– Ordering the book from the publisher

You can order a newsletter here.

Thank You

Many people have helped me to develop these topics. Wolfram Fischer introduced me to the secrets of Unix, C++ and SQL and gave me the opportunity to build my first semantic interpretation programme. Norbert Frei and his team of computer scientists actively helped to realise the concept molecules. Without Hugo Mosimann and Maurus Duelli, Semfinder would neither have been founded nor would it have been successful. The same applies to Christine Kolodzig and Matthias Kirste, who promoted and supported Semfinder in Germany. Csaba Perger and Annette Ulrich were Semfinder’s first employees, full of commitment and clever ideas and – as knowledge engineers – provided the core for the emerging knowledge base.

Wolfram Fischer actively helped me with the programming of this website. Most of the translations into English were done by Vivien Blandford and Tony Häfliger, as well as Juan Utzinger.

Thank you sincerely!