Tag Archives: Re-Entry

What is Entropy?

4. September 2024 Hans Rudolf Straub Leave a comment

Definition of Entropy

The term entropy is often avoided because it contains a certain complexity. The phenomenon entropy, however, is constitutive for everything that is going on in our lives. A closer look is worth the effort.

Entropy is a measure of information and it is defined as:

Entropy is the information
– known at micro,
– but unknown at macro level.

The challenge of this definition is:

to understand what is meant by the micro and macro states and
to understand why entropy is a difference.

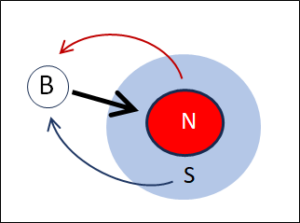
What is Meant by Micro and Macro Level?

The micro level contains the details (i.e. a lot of information), the macro level contains the overview (i.e. less, but more targeted information). The distance between the two levels can be very small (as with the bit, where the microlevel knows just two pieces of information: on or off) or huge, as with the temperature (macrolevel) of the coffee in a coffee cup, where the kinetic energies of the many molecules (microlevel) determine the temperature of the coffee. The number of molecules in the cup is really large (in the order of Avogadro’s number 10²³) and the entropy of the coffee in the cup is correspondingly high.

Entropy is thus defined by the two states and their difference. However, states and difference are neither constant nor absolute, but a question of observation, therefore relative.

Let’s take a closer look at what this relativity means for the macro level.

What is the Relevant Macro Level?

In many fields like biology, psychology, sociology, etc. and in art, it is obious to me as a layman, that the notion of the two levels is applicable to these fields, too. They are, of course, more complex than a coffee cup, so that the simple thermodynamic relationship between micro and macro becomes more complex.

In particular, it is conceivable to have a mixture of several macro-states occurring simultaneously. For example, an individual (micro level), may belong to the macro groups of the Swiss, the computer scientists, the older men, the contemporaries of 2024, etc – all at the same time. Therefore, applying entropy reasoning to sociology is not as straightforward as the simple examples like Boltzmann’s coffee cup, Salm’s lost key, or a basic bit might suggest.

Entropy as a Difference

Micro and macro level of an object both have their own entropy. But what really matters ist the difference of the two entropies. The bigger the difference, the more is unknown on the macro level about the micro level.

The difference between micro and macro level says a lot about the way we perceive information. In simple words: when we learn something new, information is moved from micro to macro state.

The conventional definition of entropy states that it represents the information present in the micro but absent in the macro state. This definition of entropy via the two states means that the much more detailed microstate is not primarily visible to the macrostate. This is exactly what Niklas Luhmann meant when he spoke of intransparency¹.

When an observer interprets the incoming signals (micro level) at his macro level, he attempts to gain order or transparency from an intransparent multiplicity. How he does this is an exciting story. Order – a clear and simple macro state – is the aim in many places: In my home, when I tidy up the kitchen or the office. In every biological body, when it tries to maintain constant form and chemical ratios. In society, when unrest and tensions are a threat, in the brain, when the countless signals from the sensory organs have to be integrated in order to recognise the environment in a meaningful interpretation, and so on. Interpretation is always a simplification, a reduction of information = entropy reduction.

Entropy and the Observer

An essential point is that the information reduction from micro to macro state is always carried out by an active interpreter and guided by his interest.

The human body, e.g., controls the activity of the thyroid hormones via several control stages, which guarantee that the resulting state (macro state) of the activity of body and mind remains within an adequate range even in case of external disturbances.

The game of building up a macro state (order) out of the many details of a micro state is to be found everywhere in biology, sociology and in our everyday live.

There is – in all these examples – an active control system that steers the reduction of entropy in terms of the bigger picture. This control in the interpretation of the microstate is a remarkable phenomenon. Always when transparency is wanted, an information rich micro state must be simplified to a macro state with less details.

Entropy can then be measured as the difference in information from the micro to the macro level. When the observer interprets signals from the micro level, he creates transparency from intransparency.

Entropy, Re-Entry and Oscillation

We can now have a look at the entropy relations in the re-entry phenomenon as described by Spencer-Brown². Because the re-entry ‘re-enters’ the same distinction that it has just identified, there is hardly any information difference between before and after the re-entry and therefore hardly any difference between its micro and macro state. After all, it is the same distinction.

However, there is a before and an after, which may oscillate, whereby its value becomes imaginary (this is precisely described in chapter 11 of Spencer-Browns book ‘Laws of Form’)². Re-entries are very common in thinking and in complex fields like biology or sociology when actions and their consequences meet their own causes. These loops or re-entries are exciting, both in thought processes and in societal analysis.

The re-entries lead to loops in the interpretation process and in many situations these loops can have puzzling logical effects (see paradoxes1 sand paradoxes2 ). In chapter 11 of ‘Laws of Form’², Spencer-Brown describes the mathematical and logical effects around the re-entry in details. In particular, he develops how logical oscillations occur due to the re-entry.

Entropy comes into play whenever descriptions of the same object occur simultaneously at different levels of detail, i.e. whenever an actor (e.g. a brain or the kitchen cleaner) wants to create order by organising an information-rich and intransparent microstate in such a way that a much simpler and easier to read macrostate develops.

We could say that the observer actively creates a new macro state from the micro state. However, the micro-state remains and still has the same amount of entropy as before. Only the macro state has less. When I comb my hair, all the hairs are still there, even if they are arranged differently. A macro state is created, but the information can still be described at the detailed micro level of all the hairs, albeit slightly altered in the arrangement on the macro level.
Re-entry – on the other hand – is a powerful logical pattern. For me, both re-entry and entropy complement each other in the description of reality. Distinction and re-entry are very elementary. Entropy, on the other hand, always arises when several things come together and their arrangement is altered or differentely interpreted.

Translation: Juan Utzinger

¹ Niklas Luhmann, Die Kontrolle von Intransparenz, hrsg. von Dirk Baecker, Berlin: Suhrkamp 2017, S. 96-120

² Georg Spencer Brown , Laws of Form, London 1969, (Bohmmeier, Leipzig, 2011)

Information, Logic

Paradoxes and Logic (Part 2)

22. August 2024 Hans Rudolf Straub Leave a comment

continues Paradoxes and Logic (part 1)

“Draw a Distinction”

Spencer-Brown introduces the elementary building block of his formal logic with the words ‘Draw a Distinction’. Figure 1 shows this very simple formal element:

Fig 1: The form of Spencer-Brown

A Radical Abstraction

In fact, his logic consists exclusively of this building block. Spencer-Brown has thus achieved an extreme abstraction that is more abstract than anything mathematicians and logicians have found so far.

What is the meaning of this form? Spencer-Brown is aiming at an elementary process, namely the ‘drawing of a distinction’. This elementary process now divides the world into two parts, namely the part that lies within the distinction and the part outside.

Fig. 2: Visualisation of the distinction

Figure 2 shows what the formal element of Fig. 1 represents: a division of the world into what is separated (inside) and everything else (outside). The angle of Fig. 1 thus becomes mentally a circle that encloses everything that is distinguished from the rest: ‘draw a distinction’.

The angular shape in Fig. 1 therefore refers to the circle in Fig. 2, which encompasses everything that is recognised by the distinction in question.

Perfect Continence

But why does Spencer-Brown draw his elementary building block as an open angle and not as a closed circle, even though he is referring to the closedness by explicitly saying: ‘Distinction is perfect continence’, i.e. he assigns a perfect inclusion to the distinction. The fact that he nevertheless shows the continence as an open angle will become clear later, and will reveal itself to be one of Spencer-Brown’s ingenious decisions. ↝ imaginary logic value, to be discussed later.

Marked and Unmarked

In addition, it is possible to name the inside and the outside as the marked (m = marked) and the unmarked (u = unmarked) space and use these designations later in larger and more complex combinations of distinctions.

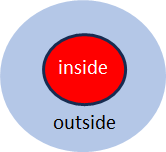
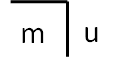Fig. 3: Marked (m) and unmarked (u) space

Distinctions combined

To use the building block in larger logic statements, it can now be put together in various ways.

Fig. 4: Three combined forms of differentiation

Figure 4 shows how distinctions can be combined in two ways. Either as an enumeration (serial) or as a stacking, by placing further distinctions on top of prior distinctions. Spencer-Brown works with these combinations and, being a genuine mathematician, derives his conclusions and proofs from a few axioms and canons. In this way, he builds up his own formal mathematical and logical system of rules. Its derivations and proofs need not be of urgent interest to us here, but they show how carefully and with what mathematical meticulousness Spencer-Brown develops his formalism.

Re-Entry

The re-entry is now what leads us to the paradox. It is indeed the case that Spencer-Brown’s formalism makes it possible to draw the formalism of real paradoxes, such as the barber’s paradox, in a very simple way. The re-entry acts like a shining gemstone (sorry for the poetic expression), which takes on a wholly special function in logical networks, namely the linking of two logical levels, a basic level and its meta level.

The trick here is that the same distinction is made on both levels. That it involves the same distinction, but on two levels, and that this one distinction refers to itself, from one level to the other, from the meta-level to the basic level. This is the form of paradox.

Exemple Barber Paradox

We can now notate the Barber paradox using Spencer-Brown’s form:

Fig. 5: Distinction of the men in the village who shave themselves (S) or do not shave themselves (N)

Fig. 6: Notation of Fig. 5 as perfect continence

Fig. 5 and Fig. 6 show the same operation, namely the distinction between the men in the village who shave themselves and those who do not.

So how does the barber fit in? Let’s assume he has just got up and is still unshaven. Then he belongs to the inside of the distinction, i.e. to the group of unshaven men N. No problem for him, he shaves quickly, has breakfast and then goes to work. Now he belongs to the men S who shave themselves, so he no longer has to shave. The problem only arises the next morning. Now he’s one of those men who shave themselves – so he doesn’t have to shave. Unshaven as he is now, however, he is a men he has to shave. But as soon as he shaves himself, he belongs to the group of self-shavers, so he doesn’t have to be shaven. In this manner, the barber switches from one group (S) to the other (N) and back. A typical oscillation occurs in the barber’s paradox – and in all other real paradoxes, which all oscillate.

How does the Paradox Arise?

Fig. 7: The barber (B) shaves all men who do not shave themselves (N)

Fig. 7, shows the distinction between the men N (red) and S (blue). This is the base level. Now the barber (B) enters. On a logical meta-level, it is stated that he shaves the men N, symbolised by the arrow in Fig. 7.

The paradox arises between the basic and meta level. Namely, when the question is asked whether the barber, who is also a man of the village, belongs to the set N or the set S. In other words:

→ Is B an N or an S ?

The answer to this question oscillates. If B is an N, then he shaves himself (Fig. 7). This makes him an S, so he does not shave himself. As a result of this second cognition, he becomes an N and has to shave himself. Shaving or not shaving? This is the paradox and its oscillation.

How is it created? By linking the two levels. The barber is an element of the meta-level (macro level), but at the same time an element of the base level (micro level). Barber B is an acting subject on the meta-level, but an object on the basic level. The two levels are linked by a single distinction, but B is once the subject and sees the distinction from the outside, but at the same time he is also on the base level and there he is an object of this distinction and thus labelled as N or S. Which is true? This is the oscillation, caused by the re-entry.

The re-entry is the logical core of all true paradoxes. Spencer-Brown’s achievement lies in the fact that he presents this logical form in a radically simple way and abstracts it formally to its minimal essence.

The paradox is reduced to a single distinction that is read on two levels, firstly fundamentally (B is N or S) and then as a re-entry when considering whether B shaves himself.

The paradox is created by the re-entry in addition to a negation: he shaves the men who do not shave themselves. Re-entry and negation are mandatory in order to generate a true paradox. They can be found in all genuine paradoxes, in the barber paradox, the liar paradox, the Russell paradox, etc.

Georg Spencer-Brown’s achievement is that he has reduced the paradox to its essential formal core:

→ A (single) distinction with a re-entry and a negation.

His discoveries of distinction and re-entry have far-reaching consequences with regard to logic, and far beyond.

Let’s continue the investigation, see: Form (Distinction) and Bit

Translateion: Juan Utzinger