Self-reference in paradoxes
(continues “Self-reference 1“)
Simple instruction for generating paradoxes
The trick with which classical logical systems can be invalidated consists of two instructions:
1: A statement refers to itself.
2: The reference or the statement contains a negation.
This constellation always results in a paradox.
A famous example of a paradox is the barber who shaves all the men in the village, except of course those who shave themselves (they don’t need the barber). The formal paradox arises from the question of whether the barber shaves himself. If he does, he’s one of those men who shave themselves and, as the statement about the barber says, he doesn’t shave those men. So he doesn’t shave himself. Therefore, he is one of the men who don’t shave themselves – and those men he shaves.
In this way, the truth of the statement, whether or not he shaves himself, constantly changes back and forth between TRUE and FALSE. This oscillation is typical of all genuine paradoxes, such as the lying Cretan or the formal proof in Gödel’s incompleteness theorem, where the truth of a statement oscillates continuously between true and false and thus cannot be determined. In addition to the typical oscillation, the barber example also clearly shows the two conditions for the true paradox mentioned above:
1. Self-reference: Does he shave HIMSELF?
2. Negation: He does NOT shave men who shave themselves.
At this point, reference can be made to Spencer-Brown, who developed a calculation that clearly demonstrates these relationships. The calculation is presented in his famous book ‘Laws of Form’. Felix Lau explained the ideas to us laymen in his book ‘Die Form der Paradoxie’.
False paradoxes (Zenon: Achilles and the tortoise)
The ‘classical’ and true paradoxes can be juxtaposed with ‘false’ paradoxes. A good example is the ‘paradox’ of Achilles and the tortoise. This false paradox does not contain a genuine logical problem, as in the case of the barber, but is based on an inappropriately chosen model which leads to Zenon’s surprising, but wrong conclusion. The times the two competitors take and the distances they run get shorter and shorter and thus approach a value that cannot be exceeded within the selected (wrong) model. This means that Achilles cannot overtake the tortoise in the model. In reality, however, there is no reason for the times and distances to be distorted in such a way.
The impossibility of overtaking the tortoise only exists in the model, which has been incorrectly selected in an ingenious way. A measurement system that distorts things in this way is of course not appropriate. In reality, it is only a duplicitous choice of model, and not a real paradox. Accordingly, the two criteria for genuine paradoxes are not present.
The crucial role of model selection
The example of Achilles and the tortoise shows the importance of a correct choice of model. The choice of model always takes place outside the representation of the solution and is not the subject of a logical proof. Rather, the choice of model has to do with the relationship of logic to reality. It takes place on a superordinate meta-level.
I postulate that the field of logic should necessarily include the choice of model and not just the calculation within the model. How do we choose a model? If logic is the study of correct thinking, then this question must also be addressed by logic.
The meta-level is necessary for choosing the model
The interaction of two levels, namely an observed level and a superordinate, observing meta-level, plays a necessary role in the choice of model, which always takes place on the meta-level which observes the lower level.
The interaction between the two levels can be observed, too. This is exactely the case in the true paradoxes, e.g. in the barber paradox. The self-reference in the true paradox inevitably introduces the two levels. This happens because an observed statement refers to itself and thus exists twice, once on the level under consideration, on which it is the ‘object’, as it were, and secondly on the meta-level, on which it refers to itself. The oscillation in the paradox arises through a ‘loop’, i.e. through a circular process between the two levels from which the logical system cannot escape – and it is oscillates because the negation makes it twist at each turn.
Selfreferential loops and paradoxes
Incidentally, there are two types of selfreferential logical loops, as Spencer-Brown and Lau point out:
- a negative one (with negation), which leads to a paradox;
- a positive one (with confirmation), which leads to a tautology.
In other words: self-reference in logical systems is always dangerous!
In order to correctly handle paradoxes in logical systems, it is worth introducing a ‘meta-leap’ – a relationship between the observed level and the meta-level.
The acceptance of the two levels and their relation is crucial for understanding the relationship between reality and formal logic.
Self-reference and first-order-logic (FOL)
Self-reference causes classical logical systems such as FOL to break down.
See also: Paradoxes and Logic
More on the topic of logic -> Logic overview page
Translation: Juan Utzinger, Vivien Blandford
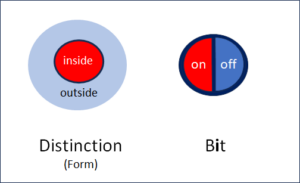
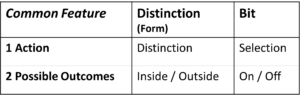
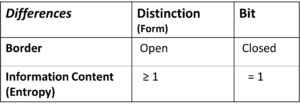

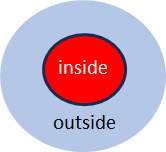
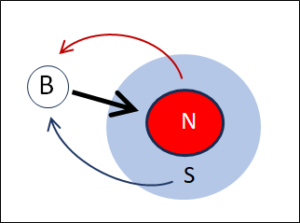
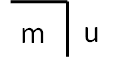 Fig. 3: Marked (m) and unmarked (u) space
Fig. 3: Marked (m) and unmarked (u) space