This is a post about the theory of the three worlds and continues the post about the perception of the octave.

Does the coincidence of the three worlds only work for the octave?

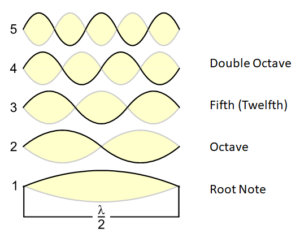
The octave demonstrates how mathematics (Platonic world) enters the physical world, and how this convergence of mathematics (integral numbers) and physics (vibrating matters) gives rise to a very special phenomenon, namely resonance. This resonance, in turn, is perceived by us human subjectively (Penrose: mental world) in quite a special way: We subjectively recognise two tones at an octave’s distance from each other as identical tones. Each of us – regardless of our cultural background – perceives a tone with twice the frequency as the “same” tone (Happy Birthday experiment).

If the frequency ratio (mathematics) deviates even only very slightly, the resonance will disappear (physics) and the tones will (mentally) strike us as different, and their simultaneous sound as a dissonance.

The octave as the first overtone thus combines the three worlds. Can we extend this success and use the further overtones following the octave for our musical scale too? The answer to this question is not a simple yes, for the mathematical series of integers has to fit in with the constraints of the physical and mental worlds.

What constraints are these? And what is a musical scale in the first place?

Constraints in the physical and mental worlds

Sounds are used to communicate, and mammals and human beings communicate acoustically. They are able to generate sounds and to hear them. These physical/mental circumstances must be taken into account if we consider how musical scales came into being.

We are unable to produce pitches of any frequency with our voices. And if two tones are far apart from their frequency, we find it difficult to measure their mutual distance (mental, subjective world). Therefore the notes of a musical scale must not be too far apart. This is the first constraint of the physical and mental world in the formation of musical scales.

This physical/mental constraint can be further substantiated and specified: since we perceive a second note an octave higher as the “same” tone (Happy Birthday experiment), a musical scale must not exceed the range of an octave. If it did, the musical scale would overlap with itself because tones outside the octave would immediately find a “same” tone within the octave. For this reason, a musical scale is always limited to the range of an octave, as is the case in all musical cultures.

On the other hand, the notes must not be too close together, for if they were, we would not be able to differentiate between them any longer. A musical scale must therefore not have any number of notes – even though this would be perfectly conceivable in mathematical terms. Yet not everything that is mathematically possible makes sense in reality.

The consequences of these conditions for musical scales can be summarised in two points:

1. The notes of a musical scale must be inside the range of an octave.
2. A musical scale must not consist of too many notes.

This is the physical/mental constraint for musical scales.

How can convincing musical scales come into being under these constraints? Can they still be scales with simple mathematical ratios?  →  next post

This is a post about the theory of the three worlds.

This is a post about the theory of the three worlds and continues the post about the resonance of the octave.

The subjective side

The mathematical world (Pythagoras) with its simple ratios and the physical world with its resonance phenomena provide us with an understanding of the octave but still fail to explain why this interval is the basis of all musical scales in all cultures. To understand this, we will also have to look at the mental world, i.e. the world of our subjective perception.

This world is accessible to everyone, but it will always remain your own and subjective perception. I can’t read your mind. Although imaging techniques such as MRI or PET are capable of observing which areas of the brain are active at what time, what they thus make perceptible is the flow of blood in a specific place, not the thought of how you experience it.

Happy Birthday

The mental world is your very personal world, but it makes quite a contribution to the primacy of the octave. Again, I propose a little experiment, not an objective one as in the preceding post, but still one that is verifiable. It has the advantage that in all likelihood, you will already have conducted it several times.

It can also be a Christmas carol in a family setting. Several people sing together, and if we are lucky, we sing with one voice. At any rate, this is usually our intention. It works better if all the singers have roughly the same register. But what if women and men and children sing together? We still recognise it if they all sing in unison. Although we do not sing in the same frequencies, but with frequencies that are an octave distant from each other, we practically don’t notice it. We perceive the distance of an octave as the same tone. If I, as a bass singing beside an alto, fail to hit the lower octave, I’m out of tune; if I do hit it, I sing in tune. This is the subjective effect of the octave: it is the same note.

The resonance in the physical world facilitates this subjective concurrence of the tones that are an octave distant from each other, and the resonance ratios on the basilar membrane of the inner ear support us in subjectively bringing the two frequencies together in our mental world, too.

First and second overtone

The octave is the first mathematically and physically possible overtone and in this respect it differs from the second overtone, which in the musical scale coincides with a fifth. To illustrate this mathematical correlation, I will again show the vibration ratios of the fundamental tone and the first overtones:

Fig. 1: Octave and fifth as overtones

Why, though, is the octave the characteristic of monophony rather than the fifth, although both of them are most closely related to the fundamental tone in mathematical and physical terms? Although mathematically the fifth is slightly farther distant from the fundamental tone than the octave, the double octave is still farther away, and yet we mentally perceive the double octave as the “same” tone as the fundamental tone, precisely like the octave.

In the mental world, i.e. in what we experience, there is a clear difference between the octave and the fifth. In this world, the octave (and all the multiple octaves) are the “same” tone, whereas the fifth is another tone. This applies all over the world, in all cultures. Since a tone which is an octave higher is perceived as the same tone, the musical scales repeat themselves an octave higher, but not a fifth.

An experiment to distinguish the octave from the fifth in the mental world

The Happy Birthday experiment described above can be extended to demonstrate the difference between the fifth and the octave, as well as the special role of the fifth. At the next birthday party, singers may try, for example, to sing the song not an octave, but a fifth lower (or higher). This is likely to be very difficult for you, precisely because you don’t sing the “same” notes as the others. And if you succeed, the others will look at you in amazement, precisely because you sing the fifth and “not the same tone”. The octave is the same tone, the fifth isn’t.

About access to the mental world

As is well known, the mental world is difficult to prove since it is completely subjective. Although all of us permanently live in this world with our thoughts and feelings, it is only indirectly accessible to objective scientific exploration. You can communicate the contents of your mental experience to other people, but you can never be quite sure that others will experience them in the same way. You can only hope that others will be able to understand your experience. Yet precisely this subjective experience and its comprehension make music so interesting: we share our subjectivity in a very specific way.

Conclusion

We can see how the mathematical, physical and mental worlds precisely meet in the octave. The uniform significance of the octave in all the world’s musical cultures can only be understood when we include all three worlds.

The next post will be about the other notes of the musical scales. Can they also be explained as simply as the octave?

This is a post about the theory of the three worlds.