As we have seen in the previous post, the tones C – D – E – G – A – C constitute the standard major pentatonic scale.
All in all, another four pentatonic scales can be created with the simple criteria for resonant pentatonic scales. These five pentatonic scales are the five musical scales which according to our mathematical criteria allow for resonances among all their tones.
We will see later on that we are able to create all the musical scales traditionally used in Europe with our pool of the nine most resonant tones. In the heptatonic scales, however, for instance in our diatonic major scale, certain tones resonate poorly with each other, which is actually more interesting in musical terms, since this creates a natural structure within the scale tones.
Conversely, pentatonic scales do not have any “wrong” tones however we mix them. It appears as if there would be no resistance, no matter which tones we sound together.
The five pentatonic scales are:
(on the basis of C)
C – D – E – G – A – C
C – D – F – G – A – C
C – Eb – F – G – Bb – C
C – Eb – F – Ab – Bb – C
C – D – F – G – Bb – C
The same tones in fractions:
(fundamental tone = 1)
1 – 9/8 – 5/4 – 3/2 – 5/3 – 2
1 – 9/8 – 4/3 – 3/2 – 5/3 – 2
1 – 6/5 – 4/3 – 3/2 – 9/5 – 2
1 – 6/5 – 4/3 – 8/5 – 9/5 – 2
1 – 9/8 – 4/3 – 3/2 – 9/5 – 2
For the purpose of the calculation, I assume that all the tones are sounded simultaneously and within an octave with the fundamental tone as the lowest tone. Thus I calculate the intervals between each tone and the fundamental tone. Then I look at the denominators of all the intervals and look for the least common multiple (lcm) of these denominators. This shows how easily resonances can occur between all the tones:
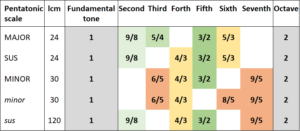
How do you read Table 1?
I have placed the same intervals of the different pentatonic scales in the same column. This results in holes in the table. Thus the major pentatonic scale does not have a fourth and a seventh. Furthermore, I have given tones with the same denominator in the fraction the same colour.
What do the colours show? – As we know, identical denominators mean that the two tones are particularly resonant because in the calculation of their frequency ratio, the two denominators “reduce themselves away” when the tones sound together. This leads to particularly simple, i.e. particularly resonant ratios between tones with the same denominator. For seconds, major thirds and fifths, I have chosen three different shades of green. The denominators are not identical but are always based on the prime number 2, which means that a reduction by two is always possible. Therefore the different greens always mix very well.
In mathematical terms, the major second has the highest denominator of all intervals in the pool – 8 – but this is not a problem. 8 is not a prime number, but 23, just as the denominator of the major third, 4, equals 22. If we sound the fifth together with the major second, the ratio of the two tones is 3/2 : 9/8 = 3×8 / 2×9 = 4/3, i.e. a fourth. The fourth is the third most resonant interval that is possible within an octave; a major second and a fifth are therefore perfectly resonant. Reduction proves effective.
Furthermore, the colours in Table 1 also show the different forms of the third and the sixth. Thus the 5/4 third is the major third and the 6/5 third is the minor third.
Musical scales are about the interval between scale tones and the fundamental tone, but also about the ratio of scales tones among each other. The lcm is the indicator of how close the resonances are in this respect. The lower the lcm, the more resonant the musical scale as a whole. However, critical tones can also be omitted or inserted into a melody as a special accent, but this is hardly possible in the standard pentatonic scales with their low lcms.
How do the five pentatonic scales differ from each other?
Major and minor scales
In functional harmony, a genuine and trailblazing European invention, the third plays an important part. Whether major or minor is a question that is always being asked. However, we are not going to deal with functional harmony (yet), but we can nevertheless look at our five pentatonic scales from the perspective of the third. We then see that we have a major pentatonic scale (with a major third) and two minor pentatonic scales (with a minor third).
The two minor pentatonic scales differ from each other in that one of them does not have a fifth. Although the lcm is the same and low in both cases, the lack of a fifth is a great handicap musically (and with regard to resonance), which is why the minor pentatonic scale without the fifth is hardly ever used. Our customary minor pentatonic scale is the one with the fifth.
When you look at Table 1, you can see the difference at once by the colours: the minor pentatonic scales has tones that are reddish in colour (denominator 5) whereas the major pentatonic scale does not. In each case, the third attracts further intervals with the same denominator. The reason for this is to be found in resonance again: identical denominators guarantee strong resonance.
Sus pentatonic scales
The term “sus” derives from “suspended fourth”. Where does the expression come from? – In classical European music, i.e. in functional harmony, the third is the crucial factor. A chord which does not have a third but has a fourth instead, is suspended, i.e. it must first be resolved; the fourth is regarded as a suspension and must be resolved into the major third. In other styles such as jazz or modern pop music, the sus chord is a chord like any other, a colour like minor and major. There are also sus musical scales without thirds, whether minor nor major, both in world music and in jazz. After the octave and the fifth, the fourth (4/3) is the most resonant interval.
Again, there are two forms of sus pentatonic scales. The high lcm of 120 of one pentatonic scale results from the fact that it has both a major second (denominator = 9) and a minor seventh (denominator = 5), which means that reduction is not possible (as you can work out for yourself if you calculate the lcm yourself). The sus pentatonic scale with the sixth has another problem: the fourth and the sixth combined with the upper fundamental tone constitute a major chord (4/3 – 5/3 – 6/3 →4-5-6). This major chord on the fourth is extremely resonant and thus becomes so dominant that the musical scale is easily misinterpreted as a major pentatonic scale.
Which pentatonic scales are commonly used?
As a consequence of the above-mentioned weaknesses of the one minor pentatonic scale and the two sus pentatonic scales, only the major pentatonic scale and the minor pentatonic scale with the fifth are commonly used. However, these two pentatonic scales are ubiquitous and very easy to sing. They can also be combined with other musical scales/chords in a melodious way, which is of particular musical interest. On their own, they sound somewhat commonplace, but show their whole strength in combinations. They are perfect building blocks for musicians.
To continue, we’ll have a look at the major musical scale. How resonant is it?
You can find an overview of the texts about the theory of the three worlds here.