Resonance works through shared overtones
Resonance occurs when two vibratory physical objects vibrate together. What matters is the two objects’ natural frequency:
- 1st degree resonance: both objects vibrate in the same frequency (f2 = f1).
- 2nd degree resonance: one object vibrates in an overtonefrequency of the other
(f2 = n * f1). - 3rd degree resonance: both objects vibrate in a shared overtone frequency
(f2 = n/m * f1).
The 3rd degree resonance reveals itself by the fact that the ratio of the two frequencies corresponds to a fraction of integers (n/m). This 3rd degree resonance is what interests us, for it has an effect on musical scales and chords rather than the 2nd degree frequency, as is often assumed (for this, cf. previous post).
Example: the fifth
One string a' has a basic frequency of 440 Hz and a string e" the frequency of 660 Hz. In this case, the second overtone on string a' vibrates with 3 × 440 = 1320 Hz and the first overtone on string e" vibrates with 2 × 660 = 1320 Hz. The overtones on the two strings have the same frequency and string a' can stimulate string e" through this common overtone. The ratio of the two basic frequencies is 3/2.
Proposition
For resonance to be generated, the frequencies must have a ratio of a fraction with integers.
Why integers?
When a vibration medium (string, basilar membrane) vibrates, standing waves are produced. These are characterised by the fact that the string does not vibrate at either end, but only in the middle, with one or several antinodes (bellies). The number of the vibration bellies in the middle must be an integer since otherwise the standing wave would not be zero at either end.
Assessing musical scale tones with the help of resonances
As we can hear, octaves and fifths can easily be made to resonate (fifth experiment) and are characterised by very simple resonance ratios (f2/f1), namely 2/1 for the octave and 3/2 for the fifth. With very few mathematical preconditions, we can now find further musical scale tones:
Criteria for the tones of a musical scale
In the cases below, we look at the interval between the tone and its fundamental tone.
- The interval must be situatedwithin an octave: this means that the fraction of the two frequencies (musical scale tone to fundamental tone) must be ≥ 1 and ≤ 2.
- The interval must be able to resonate: numerator and denominator must be integers.
- The resonance should be as vibrant as possible: the denominator of the fraction should be as small as possible.
The last two criteria are crucial but require some explanation, and I will illustrate the reasons for this later. For the time being, however, I will take all three mathematical criteria as given and see whether they enable us to find further well-known intervals.
Generation of a pool of possible musical scale tones with the help of the three criteria
We begin with the denominators, starting with denominators 1 and 2. Our musical scale already includes:

All the other tones with denominators 1 or 2 are situated outside our octave range (1-2). Therefore we look whether further well-known intervals result from denominator 3:

All the other tones with denominator 3 are situated outside our octave range. We therefore continue with denominator 4:

All the other tones with denominator 4 are situated outside our octave range. We therefore continue with denominator 5:

Any further fractions with denominator 5 are situated outside our octave range.
A thought in between
What is striking here is the fact that fractions with the numerator 7 do not exist as intervals here in Europe. My proposition is that this has something to do with the fact that seven is a prime number. This can explain why 8/5 and 9/5 are intervals that we are accustomed to although the denominator and numerators in these fractions are higher than with 7/5. Eight is 2×2×2 and nine is 3×3. We will see later that we can also compare several intervals with each other to assess the resonance. In frequency analysis, a comparison of two intervals means that the fraction of one interval is divided by the fraction of the other interval. In this situation it is of advantage that we can reduce the fraction. A prime number does not provide us with this option, but with figures such as 8 or 9, a reduction is often possible, particularly if, with fifths and fours, we have 2 or 3 in the denominator. Examples will follow.
In the case of our generation of resonant musical scale tones, however, it follows that we ignore 7/4 and 7/5 because the 7 in the numerator is too high a prime figure.
We continue with denominator 6:

Denominator 6 thus does not produce any new tones.
We omit denominator 7 as a high prime number and go directly to denominator 8:

Thus denominator 8 produces two new intervals, namely the major second (9/8 and the major seventh (15/8). The numerator and the denominator may be quite high in both fractions, but they can be divided by 2, 3 and 5. Thus the fractions of the intervals in combination with musical scales and chords become reducible, and the intervals prove to be resonant.
This is the end of our search for tones, and we can list our findings in the order of ascending frequencies:
Pool of the strongly resonating intervals
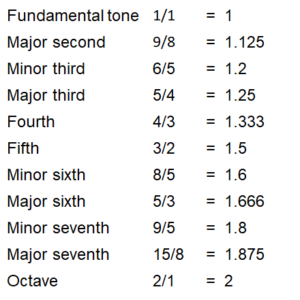
The following is striking in this pool:
a) Most intervals used by us have very simple frequency ratios.
b) The fourth, with a low denominator and numerator, is the “fourth most logical” musical scale tone. However, this tone is never an overtone. Nonetheless it makes sense, both in the mathematical world (simple fraction), in the physical world (simple resonance ratios) and mentally (subjective musical hearing experience).
c) The minor second and the tritone are missing from our pool. Mathematically speaking, these tones are not simple fractions and sound correspondingly sharper.
In music, such sharpness is interesting, because it brings change and diversity, but these intervals definitively fail to reach the ideal of a smooth resonance.
We will see later how the tritone nonetheless fits well into the resonances in certain conditions, whereas the minor second always sounds sharp and thus becomes the actual leading tone in European music.
For the time being, however, we are leaving it at our pool of ten tones. This is sufficient for many musical scales, particularly those which are used most frequently.
Further thoughts in between
As is well known, mathematicians like prime numbers. In this respect, we can define the above-mentioned criterion 3 (as small as possible numbers for numerator and denominator) more precisely:
The 3rd criterion in more precise terms:
For an interval to be able to resonate well in combination with other intervals, the prime factorisation of the numerator and the denominator should result in the smallest prime numbers possible:
2 is better than 3
3 is better than 5
5 is better than 7
7 is already too high for practical purposes.
Intervals and rhythms
This is different from rhythms, where fraction ratios also play a part. Why this is different there, and why rhythms with 7 or 11 beats sound good, can be plausibly explained with the theory of the three worlds. More about this later.
From a pool to musical scales
We now look for further criteria for attractive musical scales. The pool we have found is not a musical scale yet, but merely our starting point from which tones for different musical scales can be compiled. Here, further criteria are applicable.
Further criteria
4th criterion: preferably, the musical scale tones should also to be able to enter into resonances with each other.
5th criterion: the musical scale has a fundamental tone (a so-called tonality), which has a very special function in the musical scale.
6th criterion: the musical scale tones must not be too close to each other; if they are, we as human beings (lay people) cannot distinguish between them any longer. This is a practical constraint from the mental world. In a purely mathematical world, any number of differentiations would be conceivable; in a real situation, this is not the case. More about the criteria for musicl scales on the following page.
This is a post about the theory of the three worlds.