The ten most resonant tones within the octave
In this series of texts, we examine musical scales from the perspective of the three worlds. All three worlds are involved, as we saw, for example, when we answered the question as to why the musical scales of all musical cultures always cover precisely one octave. This cannot be explained in purely mathematical or physical terms. It is only through the involvement of the third world, namely our mental world, that the significance of the octave becomes evident.
The selection of the tones used in a musical scale is determined by all three worlds through the phenomenon of resonance, as we saw in previous posts. Let us now have a look at how the ten most resonant tones are distributed within the span of the scale octave. We will see that there are gaps in this distribution, and then think about what conclusions we can draw from this.
Here are these ten tones once again. (The table lists eleven tones, but the fundamental tone and the octave count as one tone, since the octave is both the highest tone in the present octave and simultaneously the fundamental tone of the next higher octave, in which the musical scale repeats itself.)
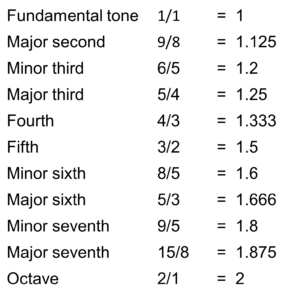
Table 1: The ten most resonant tones in an octave
The middle column of Table 1 lists the fractions which indicate the ratio between the scale tone and the fundamental tone; with the fifth, for instance, the frequency is 3/2 times the fundamental frequency. On the far right, I have expressed these fractions as decimal numbers to make comparisons easier. Of course, the numbers range from 1 (fundamental tone) to 2 (octave).
The distribution of the ten tones
To see how the ten tones are distributed within the octave, we take the frequencies of the tones and compare them with the frequency of the fundamental tone. These frequency ratios are in the right-hand column of Table 1. I have transposed these numbers into Figure 1, and you can see how the frequency ratios are arranged linearly.
This is what the arrangement of the intervals of Table 1 looks like:

Fig. 1: Frequency ratios of the potential scale tone (Table 1) in linear representation. Here, the intervals are regarded as starting from C, i. e. C = fundamental tone.
In Fig. 1, we are immediately struck by how irregular the distribution is. It displays four major gaps, namely between C and D, F and G, A and B, and H and C. Subjectively, the distribution does not appear to be , either; for example, the distance between the fundamental tone and the fourth (C-F) is much shorter than that between the fifth and the octave (G-C). However, we perceive both intervals as the same, namely as two fourths, for the distance between G and C is also a fourth, just like that between C and F. Nonetheless, the distance between G and C in Figure 1 is much longer than that between C and F. Why does the perceived distance not correspond to the real frequency ratio? – The answer is again in the exponential progression of the frequencies (physical world), which does not correspond to our linear perception (mental world). We therefore have to notate the frequencies logarithmically, thus arriving at a representation which corresponds to our subjective perception:

Fig. 2: The frequency ratios of Fig. 1 in a logarithmic representation.
We can see that in Fig. 2, the distances correspond to our subjective perception as being truer to scale. Thus, in contrast to Fig. 1, the distance between C and F is the same as between G and C, which we perceive as correct, namely as a fourth each time. The other distances in Fig. 2 also correspond to our perception.
The distribution still looks irregular, though, and there still are gaps. However, these have also shifted now. The gap between C and D has become bigger, whereas that between H and C has become smaller. What is really conspicuous are the two gaps C-D and F-G. Will we be able to do something here? Will we once more be able to resort to our reflections on resonance in order to fill the gaps? I will explain how this works in the next post.
This is a post about the theory of the three worlds.