The funnel of information reduction
In my previous article Information reduction 1, I described a chain of information processing from the patient to the flat rate per case (DRG):
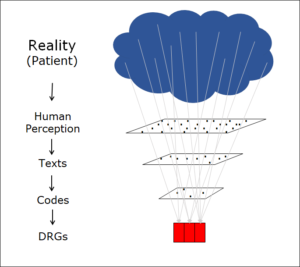
This acts as a funnel, reducing the amount of information available at each step. The extent of the reduction is dramatic. Imagine we have the patient in front of us. One aspect of a comprehensive description of this patient is their red blood cells. There are 24-30 trillion (= 24–30·1012 ) red blood cells in the human body, each with a particular shape and location in the body, and each moving in a particular way at any given time and containing a certain amount of red blood pigment. That is indeed a lot of information. But, of course, we don’t need to know all these details. As a rule, it is sufficient to know whether there is enough red blood pigment (haemoglobin) in the bloodstream. Only if this is not the case (as with anaemia) do we want to know more. Thus, we reduce the information about the patient, selecting only that which is necessary. This is entirely reasonable, even though we lose information in the process.
The funnel, quantified
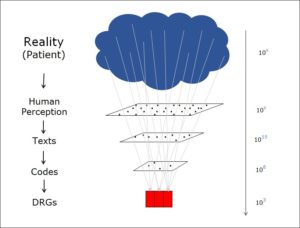
To quantify how much information reduction takes place, I have cited the number of possible states at each stage of information processing in the above figure. From bottom to top, these are as follows:
- DRGs (flat rates per case): There are various DRG systems. However, there are always about 1000 different flat rates, i.e. 103 At the level of the flat rate per case, therefore, 103 different states are possible. This is the information that is available at this level.
- Codes: In Switzerland, the ICD-10 classification system offers 15,000 different codes Let us assume, as an approximation, that each patient has two diagnoses. So we can choose between 15,000 states twice, giving 225,000,000 = 2.25 x
- 108
- .
- Texts: SNOMED, an extensive medical nomenclature, contains about 500,000 (5 x 105) different expressions. Since a medical record contains a great many words, the amount of information here is naturally much more detailed. My estimate of 1015 is definitely on the low side.
- Perception and reality: I won’t make an estimate. The above example involving red blood cells illustrates the huge amounts of information available in real-world situations.
Read more in Information reduction 3
This is a page about information reduction — see also overview.
Translation: Tony Häfliger and Vivien Blandford