Category Archives: Semantics

Semantics

The Semiotic Triangle

Leave a comment

Words and their Objects

When we speak, we use words to describe the objects in our environment. With words, however, we do not possess the objects, but only describe them, and as we all know, words are not identical to the objects they describe. It is obvious that there is no identity.

Some funny examples of the not always logical use of words can be found in the following text (in German), which explains why the quiet plays loudly and the loud plays quietly.

Fig 1: The piano (the quiet one)

Fig. 2: The lute (the wood)

But how does the relationship between words and objects look if it is not an identity? It cannot be a 1:1 relationship, because we use the same word to describe different objects. Conversely, we can use several words for the same object. The relationship is not fixed either, because the same word can mean something different depending on the context. Words change relentlessly over time, they change their sound and their meaning.

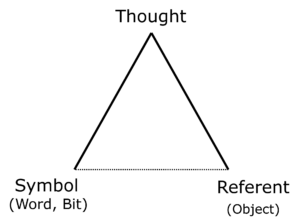
The relationship between words and designated objects is clearly illuminated by Ogden and Richards’1 famous depiction of the semiotic triangle from 1923.

The Semiotic Triangle

 

Fig 3: The semiotic triangle according to Ogden and Richards1

 

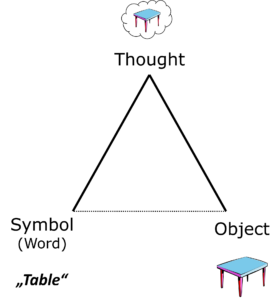
Fig 4: The semiotic triangle exemplified by the word ‘table’

The idea of the triangle has many predecessors, including Gottlob Frege, Charles Peirce, Ferdinand de Saussure and Aristotle.

Ogden and Richards use the semiotic triangle to emphasise that we should not confuse words, objects and concepts. The three points of the triangle point to three areas that are completely different in nature.

The tricky thing is that we are not just tempted but entirely justified in treating the three points as if they were identical. We want the word to describe an object precisely. We want our concepts to correspond exactly with the words we use for them. Nevertheless, the words are not the objects, nor are they concepts.

Ogden and Richards have this to say: «Between the symbol [word] and the referent [object] there is no other relevant relationship than the indirect one, which consists in the fact that the symbol is used by someone [subject] to represent a referent.»

The relationship between the word (symbol, sign) and the object (referent) is always indirect and runs via someone’s thought, i.e. the word activates a mental concept in ‘someone’, i.e. a human subject, speaker or listener. This inside image is the concept.

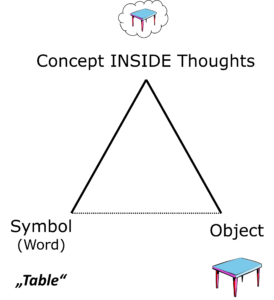
Fig. 5: This is how Ogden and Richards see the indirect relationship between symbol and indicated object (referent). The thoughts contain the concepts.

The diminished baseline in Fig. 5 can also be found in the original of 1923. Symbol (word) and referent (reference object) are only indirectly connected via the thoughts in the interpreting subjects. This is where the mental concepts are found. The concepts are the basic elements of our thoughts.

When we deal with semantics, it is essential to take a look at the triangle. Only the concepts in our head connect the words with the objects. Any direct connection is an illusion.

This is a post on the topic of semantics.

Translation: Juan Utzinger

1 Ogden C.K. und Richards I.A. 1989 (1923): The Meaning of Meaning. Orlando: Harcourt.

Semantics, Theory of the Three Worlds

The mental world

Leave a comment

What is the mental world?

The mental world is the world in our heads. It is the way in which we perceive the world; it consists of our sensations, feelings and thoughts. It is a completely subjective world.

In the theory of the three worlds, the mental world is the third world besides the physical and the Platonic worlds.

Difference from the physical world

Whereas the physical world is objectively comprehensible, the mental world remains subjective.

In other words: whereas we can observe the objects of the physical world from the outside, this is impossible with the objects of the mental world.

The example of colour

Objectively (physically), colours can be measured as wavelengths of light waves. Thus yellow and blue, for instance, have specific wavelengths, which can be objectively measured in nanometres. What we perceive, however, is not the wavelength. We have a subjective impression of yellow or blue, which is actually triggered off by the physical phenomenon of the light wave, yet what we sense is not the wavelength, but a very subjective impression of a yellow or blue colour. Thus we perceive green, for example, as a very specific colour which corresponds to a certain wavelength. As we know from our art lessons, however, green can be mixed from blue and yellow. This means that what hits our eyes physically is a combination of photons with a “blue” and “yellow” wavelength. However, we do not perceive these two objectively existing wavelengths, but we apprehend the combination as green, i.e. as a completely different wavelength. This subjective impression is called qualia in the literature.

Does the mental world really exist?

Or is it simply an emanation of the physical world? Many people believe that it is. The subjective impression that we sense is generated in the brain by electrical currents triggered by photons on our retina. In these terms, the mental world does not really exist but is an emanation of the physical world, a mere effect of physics which makes us believe that we see a colour.

At the other end of the spectrum, we find the solipsists and the radical constructivists such as Ernst von Glasersfeld. For solipsists, the mental world – i.e. their own imagination – is the only world that exists with certainty. Everything else can be deception, a dream; only one’s own imagination is certain.

Thus we have two extremes
  1. a) Physicalists: only the physical world exists; the mental world is wholly constructed out of the physical world.
  2. b) Solipsists: only the mental world exists; it fakes the existence of an external physical world.

What is more interesting than these two extremes are the opinions in between. Roger Penrose, for instance, advocated with his theory of the three worlds that none of the three worlds should be excluded as non-existing. Rather, he wanted to clarify the interrelations of the three worlds.

Coexistence

This is also my stance: although it seems plausible to see mental sensations and processes as mere effects of the physical world, it strikes me as sensible to view the mental world as a world of its own – not because it could not have emanated from the physical world but because it can be described better in this way. To return to the example of the colours: it is irrelevant to human behaviour whether green is generated by its own green wavelength or by a combination of yellow and blue wavelengths; I always see the same colour and also behave accordingly. The description of human thought, perception and behaviour becomes at once simpler and more precise if we tackle the processes in the mental world directly. This is possible, but only from the inside, if I imagine the thoughts, colours, etc. of the mental world myself.

Communication about mental objects (thoughts, colours, etc.) is possible, too, but also requires a subjective basis of experience; this time, one that the interlocutors have experienced in a similar way.

Where does the mental world play a part?

Wherever inner perceptions and processes are involved, we are in the mental world.

The following areas can hardly be described without accepting the existence of the mental world:

  • psychology,
  • culture,
  • values, morality,
  • politics,
  • art.

Thus the mental world is not quite irrelevant.

Semantics

In my own field, semantics, a clear dividing line between the objective and the subjective worlds can be discerned. Whereas words and sentences are part of the objective world, the concepts, i.e. the meanings of the words, and the thoughts that are expressed by means of the sentences, are part of the subjective, i.e. mental world.

This is a post about the theory of the three worlds.

Semantics

Semantics and Linguistics

Leave a comment
What is semantics?

A simple and easily understandable answer is that semantics is the meaning of signals. The signals can exist in any form: as text, as an image, etc. The most frequently studied semantics is that of words.

This is a good reason to examine the relationship of linguistics and semantics. Can semantics be regarded as a subdiscipline of linguistics?

Linguistics and semantics

Linguistics, the science of language and languages, has always examined the structure (grammar, syntax) of languages. Once the syntax of a sentence has been understood, linguists see two further tasks, i.e. secondly to examine the semantics of the sentence and thirdly to examine its pragmatics. “Semantics” is about the meaning of sentences, “pragmatics” about the “why” of a statement.

The linguists’ three steps

In the linguists’ eyes, there are thus three steps in understanding language: syntax -> semantics -> pragmatics. These three fields are weighted very differently by linguists: a conventional textbook predominantly deals with syntax, whereas semantics and pragmatics play a marginal role – and always on the basis of the previously conducted syntactic analysis. The linguists’ syntactic analysis thus already sets the course for what is based on it, namely semantics and pragmatics.

This is not really ideal for semantics. When you deal with semantics in more detail, it becomes clear that the grammar and other properties of individual languages constitute externals which may circumscribe the core of the statements – their meaning – in an occasionally very elegant manner, but they merely circumscribe them and do not represent them completely, let alone directly. A direct formal representation of what is meant by a text, however, would be the actual objective of a scientific semantics.

Can this objective be attained? First, we will have to clarify the relationship between words and concepts – words and concepts are not the same. Concepts are the basic elements of semantics and have a special, but not entirely simple relationship with the words of a language.

Word does not equal concept

One could flippantly assume that there is a one-to-one relationship between words and concepts, i.e. that behind every word, there is a concept which summarises the meaning of the word. But this is precisely what is wrong. Words and concepts cannot unequivocally be mapped on each other. The fact that this is the case can be recognised by everybody who observes himself while reading, talking and thinking.

It is obvious that a word can have several meanings depending on the context in which it is uttered. Occasionally, a word may even have no meaning at all, for instance if it is a technical term and I don’t know the specialist field. In such a case, I may be able to utter the word, but it remains devoid of meaning for me. Yet somebody who understands the specialist field will understand it.

Meaning has much to do with the addressee

Even perfectly normal words which we all know, not always have an unequivocal meaning but can evoke slightly different ideas (meanings) depending on the listener or the context. This does not only concern abstract words or words to which various values are attached, such as happiness, democracy, truth, etc.: absolutely concrete terms like leg, house and dog are interpreted differently by different people, too. The reception of the words as meaningful concepts has much to do with the addressee, his situation and expectations. There is definitely no 1:1 relation between words and concepts.

Meanings vary

Even in ourselves, there are quite different ideas for the same word; depending on the situation, we associate different ideas with the same word, depending on the situation and the everchanging state of our momentary knowledge of words and topics.

A dynamic process

The transition from one language to another shows how the link between words and concepts is a dynamic process in time and changes the meaning of the words. The English word ‘brave’ is the same word as the word ‘bravo’ in Italian, which we use if a musical performance inspires us. But the same word also exists in German, where today it means prissy or well-behaved – certainly not exactly the same as brave, though it is the same word and once meant the same in German as in English.

Semantics examines the play of meanings

We have to accept that a word and a concept cannot be mapped on each other just like that. Although in individual cases it may seem that there is precisely one concept (one semantics) behind every word, this idea is completely inappropriate in reality. And it is this idea which prevents the play of meanings from being understood correctly. Yet it is precisely this play of meanings which, in my view, constitutes semantics as a field of knowledge. In this field, it is possible to represent concepts formally in their own proper structure – which is completely independent from the formal representation of words.

Translation: Tony Häfliger and Vivien Blandford

Information, Semantics

Two Types of Coding 2

Leave a comment
The two types of coding in set diagrams

I would like to return to the subject of my article Two types of coding 1 and clarify the difference between the two types of coding using set diagrams. I believe this distinction is so important for the field of semanticsand for information theory in general, that it should be generally understood.

Information-preserving coding

The information-preserving type of coding can be represented using the following diagram

Mengendiagramm 1:1-Kodierung

Fig 1: Information-preserving coding (1:1, all codes reachable)

The original form is shown on the left and the encoded form on the right. The red dot on the left could, for example, represent the letter A and the dot on the right the Morse code sequence dot dash. Since this is a 1:1 representation, you can always find your way back from each element on the right to the initial element on the left, i.e. from the dot dash of Morse code to the letter A.

Mengendiagramm 1:1-Kodierung, nicht alle Kodes erreicht

Fig. 2: Information-preserving coding (1:1, not all codes reachable)

Of course, a 1:1 coding system preserves information even if not all codes are used. Since the unused ones can never arise during coding, they play no role at all. For each element of the set depicted on the right that is used for a code, there is exactly one element in the initial form. The code is therefore reversible without loss of information, i.e. decodable, and the original form can be restored without loss for each resulting code.

Mengendarstellung: Informationserhaltende Kodierung (1:n)

Fig. 3: Information-preserving coding (1:n)

With a 1:n system of coding, too, the original form can be reconstructed without loss. An original element can be coded in different ways, but each code has only one original element. There is thus no danger of not getting back to the initial value. Again, it does not matter whether or not all possible codes (elements on the right) are used, since unused codes never need to be reached and therefore do not have to be retranslated.

For all the coding ratios shown so far (1:1 and 1:n), the original information can be fully reconstructed. It doesn’t matter whether we choose a ratio of 1:1 or 1:n, or whether all possible codes are used or some remain free. The only important thing is that each code can only be reached from a single original element. In the language of mathematics, information-preserving codes are injective relations.

Information-reducing coding
Mengendiagramm: Informationsreduzierende Kodierung

Fig. 4: Information-reducing coding (n:1)

In this type of coding, several elements from the initial set point to the same code, i.e. to the same element in the set of resulting codes. This means that the original form can no longer be reconstructed at a later time. The red dot in the figure on the right, for example, represents a code for which there are three different initial forms. The information about the difference between the three dots on the left is lost in the dot on the right and can never be reconstructed. Mathematicians call this a non-injective relation. Coding systems of this type lose information.

Although this type of coding is less ‘clean’, it is nevertheless the one that interests us most, as it typifies many processes in reality.

Information, Semantics

Two Types of Coding 1

Leave a comment
A simple broken bone

In the world of healthcare, medical diagnoses are encoded to improve transparency. This is necessary because they can be formulated in such a wide variety of different ways. For example, a patient may suffer from the following:

– a broken arm
– a distal radius fracture
– a fractura radii loco classico
– a closed extension fracture of the distal radius
– a Raikar’s fracture, left
– a bone fracture of the left distal forearm
– an Fx of the dist. radius l.
– a Colles fracture

Even though they are constructed from different words and abbreviations, all the above expressions can be used to describe the same factual situation, some with more precision than others. And this list is by no means exhaustive. I have been studying such expressions for decades and can assure you without any exaggeration whatsoever that there are billions of different formulations for medical diagnoses, all of them absolutely correct.

Of course, this  huge array of free texts in all variations cannot be processed statistically. The diagnoses are therefore encoded, often using the ICD (International Classification of Diseases) system, which comprises between 15,000 and 80,000 different codes depending on variant. That’s a lot of codes, but much clearer than the billions of possible text formulations it replaces.

Incidentally, the methods used to automate the interpretation of texts so that it can be performed by a computer program are a fascinating subject.

Morse code 

Morse code is used for communication in situations where it’s only possible to send very simple signals. The sender encodes the letters of the alphabet in the form of dots and dashes, which are then transmitted to the recipient, who decodes them by converting them back into letters. An E, for example, becomes a dot and an A becomes a dot followed by a dash. The process of encoding/decoding is perfectly reversible, and the representation unambiguous.

Cryptography

In the field of cryptography, too, we need to be able to translate the code back into its original form. This approach differs from Morse code only in that the translation rule is usually a little more complicated and is known only to a select few. As with Morse code, however, the encrypted form needs to carry the same information as the original.

Information reduction

Morse code and cryptographic codes are both designed so that the receiver can ultimately recreate the original message. The information itself needs to remain unchanged, with only its outer form being altered.

The situation is quite different for ICD coding. Here, we are not dealing with words that are interchangeable on a one-for-one basis such as tibia and shinbone – the ICD is not, and was never intended to be, a reversible coding system. Instead, ICD codes are like drawers in which different diagnoses can be placed, and the process of classification involves deliberately discarding information which is then lost for ever. This is because there is simply too much detail in the diagnoses themselves. For example, a fracture can have the following independent characteristics:

– Name of the bone in question
– Site on the bone
– State of the skin barrier (open, closed)
– Joint involvement (intra-articular, extra-articular)
– Direction of the deformity (flexion, extension, etc.)
– Type of break line (spiral, etc.)
– Number and type of fracture fragments (monoblock, comminuted)
– Cause (trauma, tumour metastasis, fatigue)
– etc.

All these characteristics can be combined, which multiplies the number of possibilities. A statistical breakdown naturally cannot take all combination variants into account, so the diagnostic code covers only a few. In Germany and Switzerland, the ICD can cope with fewer than 20,000 categories for the entire field of medicine. The question of what information the ‘drawers’ can and cannot take into account, is an important topic both for players within the healthcare system and those of us who are interested in information theory and its practical application. Let’s turn now to the coding process.

Two types of coding

I believe that the distinction described above is an important one. On the one hand, we have coding systems that aim to preserve the information itself and change only its form, such as Morse code and cryptographic systems. On the other hand, we have systems such as those for encoding medical diagnosis. These aim to reduce the total amount of information because this is simply too large and needs to be cut down – usually dramatically – for the sake of clarity. Coding to reduce information behaves very differently from coding to preserve information.

This distinction is critical. Mathematical models and scientific theories that apply to information-preserving systems are not suitable for information-reducing ones. In terms of information theory, we are faced with a completely different situation.