When does resonance occur?
Resonance between two physical media depends on the frequency ratio of their natural vibrations. When the two frequencies constitute a simple fraction such as 2/1 or 3/2, resonance can occur. In an earlier post, I explained how the ten simplest frequency ratios lead with mathematical necessity to the ten tones which appear in our musical scales, no matter whether they are major scales, the various minor scales, the ecclesiastical modes, the major pentatonic scales, the minor pentatonic scales, the blues scale, etc. Ten tones are sufficient to build all these different scales.
Pure intonation and temperament
However, does resonance also work in the equal temperament? In the post about the tempered scale, we saw how the two distributions differ. Fig. 1 shows the pure intonation in blue – i.e. the ten most resonant intervals plus the two fillers C sharp and F sharp – and below, the twelve intervals of the equal temperament in red.
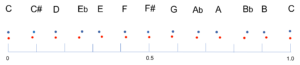
Fig. 1: Pure intonation (blue) and equal temperament (red) with fundamental tone C (logarithmical representation)
Obviously, the frequency ratios of the equal temperament differ from those of the pure intonation and thus no longer correspond to the simple frequency ratios which originally resulted in our pure musical scales. Nonetheless, the impure intonation works, and we distinguish between minor and major thirds, fifths and sixths although they are not pure any longer. Are the tempered, i.e. impure intervals still resonant?
The answer is an unequivocal yes.
Why the impure temperament is still resonant
Fig. 2 below shows resonance as dependent on frequency relation and damping. The greater the damping, the lower the resonance.
What is interesting is how the frequency ratios – in Fig. 2 marked on the horizontal from 0.0 to 3.0 – impact on the emergence of resonance. Resonance is strongest at 1.0, i.e. when both media, the stimulating and the stimulated, have an identical frequency. Yet resonance occurs even if the frequency ratio is not precisely 1. This is the reason why we experience the tempered scale as resonant, too.
Fig. 2: Resonance as a function of the precision of frequency ratios
[Source: https://en.wikipedia.org/wiki/Resonance (22/Feb/2022)]
As we can see in Fig. 2, the tempered scale with its not quite precise fractions still leads to resonances between the intervals, albeit to slightly weaker ones. Since we practically only hear music that is based on the tempered scale, we have become accustomed to it. Pure intonation can only be produced by instruments which can alter the pitches . It does not work on keyboard instruments. Pure string ensembles or unaccompanied singers are able to make music with pure intonation, and good ensembles actually do so.
Additional effects of the tempered scale
The key benefit of the temperament is the immense extension of compositional possibilities.
There are, however, further additional effects: the fact that the intervals are slightly “out of tune” leads to interferences (beats), with resonance ebbing and surging. The friction between two impurely tuned tones can result in the emergence of a third tone, which overlays the other two. Such effects can also be consciously sought in pure intonation in that a singer or instrumentalist slightly alters the pitch, thus creating a conscious musical effect with which they can play.
However, I don’t want to expand on these effects, nor on the interesting effects which piano tuners have to take into consideration, such as the so-called stretching across the whole range of tones. Tuning, for instance of a piano, has to keep several goals in view at the same time. Here, too, the three worlds have a simultaneous impact: the mathematics of the pure figures, the physics of the real piano strings and our subjective impression.
It is for two reasons, however, that I won’t pursue these considerations here. Firstly, the above-mentioned acoustic phenomena have been described very well, and secondly by experts who have specialised in them and know substantially more than a computer scientist and amateur musician like me. To me, the equal temperament is simply an ingenious and practical invention which I readily accept because it distinctly extends the harmonic possibilities of music.
I will therefore continue this series with the extensions of the compositional possibilities that result from the equal temperament.
This is a post about the theory of the three worlds.