Tag Archives: Information Reduction

Artificial Intelligence, Logic

Information Reduction 8: Different Macro States

Leave a comment
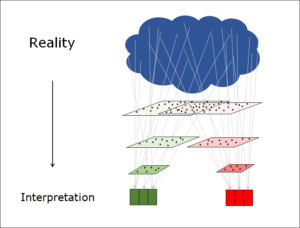
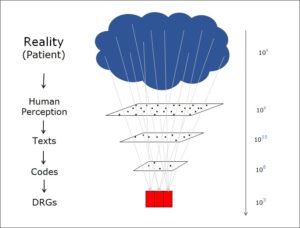
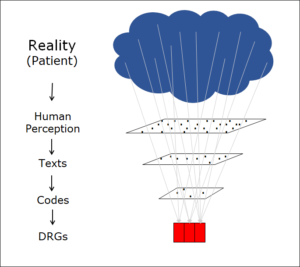
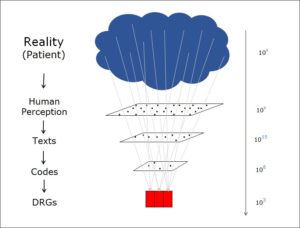
Two states at the same time

In my last article I showed how a system can be described at two levels: that of the micro and that of the macro state. At the micro level, all the information is present in full detail; at the macro level there is less information but what there is, is more stable. We have already discussed the example of the glass of water, where  the micro state describes the movement of the individual water molecules, whereas the macro state encompasses the temperature of the liquid. In this paper I would like to discuss how different the relationship between micro and macro states can be.

Does the macro state depend on the micro state?

In terms of its information content, the macro state is always smaller than the micro. But does it have an existence of its own at all, or is it simply a consequence of the micro state? To what extent is the macro state really determined by the micro state? In my opinion, there are major differences between the different situations in this respect. This becomes clear when we consider the question of how to predict the future of the systems.

Glass of water

If we know the kinetic energy of the many individual molecules that make up a glass of water, we also know its temperature – the macro state can be deduced from knowledge about the micro state. In this case, we also know how it will develop: if the system remains closed, the temperature will remain constant. The macro state remains the same, even though there is a lot of information speeding around in the micro state. The temperature only changes when external influences – and in particular energy flows – come to bear. So, why does the temperature remain the same? It all comes down to the law of conservation of energy. The total amount of energy in the closed system remains constant, which means that however the variables in the micro state change, the macro state remains the same.

But why does the law of conservation of energy apply? This is closely linked to the Hamilton principle or principle of least action. This is one of the most fundamental rules in nature and by no means confined to thermodynamics.

The closed thermodynamic system is an ideal system that hardly ever occurs in such a pure form in nature; in reality, it is always an approximation. Let us now compare this abstract system with some systems that really do exist in the natural world.

Water waves and Bénard cells

This type of system can be observed as a wave on the surface of a body of water. In my opinion, Bénard cells, as described in the work of Prigogine, fall into the same category. In both cases, the macroscopic structures come into being as open systems. Both cells and waves can only arise due to external influences, with Bénard cells forming due to temperature gradient and gravity, and water waves forming due to wind and gravity. The structures arise due to the effects of these external forces, which interact to produce macroscopic structures that, interestingly enough, remain in place for long periods. Their persistence is astonishing. Why does the wave maintain its shape, when the particles of matter it is made up of are constantly changing?

The macroscopic structures formed in such open systems are much more complex than those of an isolated thermal system. Opposing external forces (such as wind and gravity) give rise to completely new forms – waves and cells. The external forces are necessary for the form to emerge and persist, but the resulting macroscopic form itself is new and is not inherent to the external forces, which are very simple in terms of information content.

Just like in the thermal system, we have two levels here: the macro level of the simple outer form (cell or wave) and a micro level of the many molecules that make up the body of this form. And, once again, the macro level – i.e. the form – is much simpler in terms of information content than the micro level, which consists of a huge number of molecules. The wave retains its shape over a long period of time, while the underlying molecules move about frantically. The wave continues to roll, capturing new molecules along the way, which now make up the wave. At given any moment the form, i.e. the coming together of the macro state from the individual molecules, appears completely determined. The information that makes up the form, however, is much easier to grasp at the macro level. The movements of the many individual molecules that make up the wave are there, but do not seem necessary to describe the form of the wave. It looks as though the new macro state is best explained by the old one.

In contrast to more highly developed organisms, the structure of both water waves and Bénard cells disappears as soon as the forces from outside diminish. Our own existence, like that of any other organic life, depends on structures that are much slower to disappear. That is to say: the macro state needs strengthened in relation to the micro state.

The thermostat

The macro state can be bolstered by giving it a controller. Imagine a heating system with a temperature sensor. When the temperature drops, the heating comes on; when it gets too high, the heating goes off. This keeps the temperature, i.e. the macro state, constant. But, of course, this heating system is anything but closed from a thermodynamic point of view. And temperature sensors and control systems to support the macro state and keep it constant are a human invention, not a naturally occurring phenomenon like water waves. Does such a thing exist in the natural world?

Autopoiesis and autopersistence

Of course, such control systems are also found in nature. During my medical studies I was impressed by the number and complexity of control circuits in the human organism. Control is always based upon information. The study of medicine made it evident to me that information is an essential part of the world.

The automatic formation of the wave or Bénard cell is a phenomenon known as autopoiesis. Waves and cells are not stable, but biological organisms are – or, at any rate, they are much more stable than waves. This is because biological organisms incorporate their own control systems. It’s as if a wave were to become aware of its own utter dependency on the wind and respond by actively seeking out its source of sustenance (the wind) or by creating a structure within itself to preserve its energy for the lean times when the wind is not blowing.

This is exactly what the human body – and in fact every biological body – does. It is a macro state that can maintain itself by controlling its micro state and deploying control processes in response to its environment.

Biological systems

This type of system differs from insulated thermal systems by its ability to create shapes, and from simple, randomly created natural shapes such as a water wave by its ability to actively assist the shape’s survival. This is because biological systems can respond to their environment to ensure their own survival. Biological systems differ from the simpler autopoietic systems in their ability to maintain a constant shape for longer thanks to complex internal controls and purposeful activity in response to their environment.

If a system is to maintain a constant form, it needs some kind of memory to preserve the pattern. And, if it is to respond purposefully to its environment, it helps if it has some kind of idea about this outside world. Both this memory of its own pattern and the simplified idea about the outside world need to be represented as information within the biological system information, otherwise it will not be able to maintain its form over time. The biological system thus has some kind of information-based interior. Because of the properties described above, biological systems are always interpreting systems.

This is an article from the series Information reduction.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 7: Micro and Macro State

Leave a comment

Examples of information reduction

In previous texts we looked at examples of information reduction in the following areas:

  • Coding / classification
  • Sensory perception
  • DRG (Flat rate per case)
  • Opinion formation
  • Thermodynamics

What do they have in common?

Micro and macro state

What all these examples have in common is that, in terms of information, there are two states: a micro state with a great many details and a macro state with much less information. One very clear example that many of us will remember from our school days is the relationship between the two levels in thermodynamics.

The two states exist simultaneously, and have less to do with the object itself than with the perspective of the observer. Does he need to know everything, down to the last detail? Or is he more interested in the essence, i.e. the simplified information of the macro state?

Micro and macro state in information theory

The interplay of micro and macro states was first recognised in thermodynamics. In my opinion, however, this is a general phenomenon, which is closely linked to the process of information reduction. It is particularly helpful to differentiate between the two states when investigating information processing in complex situations.
Wherever the amount of information is reduced, a distinction can be drawn between a micro and a macro state. The micro state is the one that contains more information, the macro state less. Both describe the same object, but from different perspectives.

The more detailed micro state is considered to be ‘more real’

We tend to think we are seeing something more clearly if we can discern more details. So we regard the detailed micro state as the actual reality and the macro state as either an interpretation or a consequence of this.

… but the low-information macro state is more interesting

Remarkably, however, the low-information state is of more interest to us than the micro state. In the micro state, there are simply too many details. These are either irrelevant to us (thermodynamics, sensory perception) or they obstruct our clear view of the goal represented by the macro state (coding, classification, opinion-forming, flat rate per case).

Strange antagonism

There is thus a strange antagonism between the two states, with one seeming more real and the other more relevant, as if these two qualities were somehow at odds with one another. The more detailed the information, the less the many single data points have to do with the overall perspective, which thus increasingly disappears from sight. On the other hand: the more intensively the view strives for relevance, the more it detaches itself from the details of reality. This paradoxical relationship between micro and macro state is characteristic of all information reduction relationships and highlights both the importance of, and the challenges associated with, such processes.

Are there differences between the various processes of information reduction?

Absolutely. The only thing they have in common is that it is possible to display the data at a detailed micro level or at a macro level containing little information, with the latter usually being more relevant.

Such processes always involve a reduction in information, but the way in which it is reduced differs. At this point it would be illuminating to examine the differences – which play a decisive role in many issues – more closely. Read more in next post.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 6: The Waterglass, Revisited

Leave a comment

Is that physics?

In my article Information reduction 5: The classic glass of water, I drew upon the example of a glass of water to illustrate the principle of information reduction. In this example, the complex and detailed information about the kinetic energy of water molecules (micro level) is reduced to simple information about the temperature of the water.

Of course, a physicist might criticise this example – and quite rightly so, because the glass of water is actually much more complicated than this. Boltzmann’s calculations only apply to the ideal gas, i.e. one whose molecules do not interact except when they collide and exchange their individual movement information.

An ideal gas

The ideal gas is an idealisation you won’t find anywhere in the real world. Other forces exist between individual molecules than the purely mechanical ones, and the situation in our glass of water is no different. Because water is a liquid not a gas and because much stronger bonds exist between molecules in liquids than between gas molecules, these additional bonds complicate the picture.

Water

Moreover, water is a special case. The water molecule (H2O) is a strong dipole, which means it has a strong electrical charge difference between its two poles, the negatively charged pole with the oxygen atom (O) and the positively charged pole with the two hydrogen atoms (H2). As a result of this strong polarity, multiple water molecules join together. If such agglomerations were to be maintained, the water would be a solid (such as ice) rather than a liquid. But since they are only temporary, the water remains a liquid, but a special one that behaves in a very particular way. See, for example, the current research of Gerald Pollack.

Physics and information science

A glass of water probably isn’t the example a physicist would have chosen, but I’m not going to change it. It’s as good an example as any to explain the ratio of information at the micro and macro levels. Boltzmann’s calculations are only approximately correct, but his thesis holds: the temperature of an object is the macro-level information that summarises the many data points about the chaotic movements of the individual molecules at the micro level.

The glass of water may be a bad example to a physicist.  For our consideration about micro and macro states, however, it makes no difference whether we are considering an ideal gas or a glass of water: there is always a huge information gap between the macro state and the micro state, and that is the salient point. In a glass of water, the micro state contains billions of times more information than the macro state. And, interestingly, although the micro state is richer in information, it is the macro state that is of greater interest to us.

The transition

How does the transition from micro to macro state take place in different cases? Clearly, this transition is slightly different in the glass of water than in the ideal gas due to the special properties of the H2O molecule. And the transition from the micro to the macro state is completely different in our other examples of classification, concept formation and framing that are not drawn from the physical world. We will now go into these peculiarities. See the posts to come.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 5: The Classic Glass of Water

Leave a comment
Information reduction in thermodynamics

A very specific example of information reduction can be found in the field of thermodynamics. What makes this example so special is its simplicity. It clearly illustrates the basic structure of information reduction without the complexity found in other examples, such as those from biology. And it’s a subject many of us will already be familiar with from our physics lessons at school.

What is temperature?

A glass of water contains a huge amount of water molecules, all moving at different speeds and in different directions. These continuously collide with other water molecules, and their speed and direction of travel changes with each impact. In other words, the glass of water is a typical example of a real object that contains more information than an external observer can possibly deal with.

That’s the situation for the water molecules. So what is the temperature of the water in the glass?

As Ludwig Boltzmann was able to demonstrate, temperature is simply the result of the movement of the many individual water molecules in the glass. The faster they move, the more energy they have and the higher is the temperature of the water As Ludwig Boltzmann explained, the temperature of the water in the glass can be calculated statistically from the kinetic energy of the many molecules. Billions of molecules with their constantly changing motion produce exactly one temperature. Thus, a large amount of information is converted into a single fact.

The micro level and the macro level

It’s worth noting that the concept of temperature cannot be applied to individual molecules. At this level, there is only the movement of many single molecules, which changes with each impact. The kinetic energy of the molecules depends on their speed and thus changes with each impact.

Although the motion of the water molecules is constantly changing at the micro level, the temperature at the macro level of the glass of water remains comparatively constant. And, in the event that it does change, for example because heat is given off from the water at the walls of the glass, there are formulas that can be used to calculate the movement of the heat and thus the change in temperature. These formulas remain at the macro level, i.e. they do not involve the many complicated impacts and movements of the water molecules.

The temperature profile can thus be described and calculated entirely at the macro level without needing to know the details of the micro level and its vast number of water molecules. Although the temperature (macro level) is defined entirely and exclusively by the movement of the molecules (micro level), we don’t need to know the details to predict its value. The details of the micro level seem to disappear at the macro level. This is a typical case of information reduction.

In the next post I’ll make some precisions concerning the waterglass.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 4: Framing

Leave a comment
Framing matters

The framing effect is a topic that comes up a lot these days. Framing is the phenomenon whereby the same message is perceived differently, depending on what additional information is sent with it. The additional information is provided to give the message the right ‘frame’ so that recipients respond appropriately.

Even if the additional information is undoubtedly true, the recipient can be genuinely manipulated by framing, simply by the selection of details that are in themselves factually correct. Framing is, of course, used in advertising, but its role in political reporting has become something of a hot topic of late.

Of course, framing in politics and advertising always involves choosing words that connect an item of information to the corresponding emotional content. But the simple fact that some aspects (details) of events are drawn into the foreground and some pushed into the background changes the image that the recipient forms of the message. For example, our response to the fact that a lot of refugees/migrants want to come to Europe depends on which of the many people we have in mind and which of the diverse range of aspects, reasons, circumstances and consequences of their journey we focus on. Reports about the criminal activities of individual migrants evoke a completely different image from descriptions of the inhuman, unfathomably awful conditions of the journey. That people are coming is a fact. But the way this fact is evaluated – its interpretation – is a matter of simplification, i.e. the selection of data. This brings us clearly to the phenomenon of information reduction.

Framing and information reduction

Real-world situations always contain much more detail than we can process. And because this means we always need to simplify them, information selection plays a crucial role: what do we bring to the forefront and what do we push into the background? The answer to this question colours our perception and thus our opinion. This phenomenon of information reduction is the same as that encountered in medical coding, where a variety of characteristics are drawn upon – or disregarded – in the assignment of codes (see article Two types of coding 1). The reduction and selection of information is part of all perception processes, and our actions and decisions are always based upon simplifications. The selection of details is what shapes our perception, and this selection depends not upon the object being viewed, but on the subject making the selection.

Diverging interpretations are possible (see previous article)

Reality (top of the diagram) is made up of all the facts, but our interpretation of it is always based upon a selection from this vast array of detail. This may lead us to form a range of different opinions. I believe that this phenomenon of information reduction (the interpretation phenomenon) is both fundamental and inescapable, and that it plays an important role in a wide range of different contexts. The framing effect is a typical example, but it is one of many.

Links to framing (in German):
– Spiegel article “Ab jetzt wird zurückgeframt” of 22.2.2019
– Wikipedia.de on the framing effect
– Interview with communication trainer Benedikt Held

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 3: Information is Selection

Leave a comment
Information reduction is everywhere

In a previous post, I described how the coding of medical facts – a process that leads from a real-world situation to a flat rate per case (DRG) – involves a dramatic reduction in the amount of information:

Informationsreduktion

Information reduction

This information reduction is a very general phenomenon and by no means limited to information and its coding in the field of medicine. Whenever we notice something, our sensory organs – for example our retinas – reduce the amount of information we take in. Our brain then simplifies the data further so that only the essence of the impressions, the part that is important to us, arrives in our consciousness.

Information reduction is necessary

If you ask someone how much they want to know, most people will tell you that they want to know as much as possible. Fortunately, this wish is not granted. Many will have heard of the savant who, after flying over a city just once, was able to draw every single house correctly from memory. Sadly, the same individual was incapable of navigating his everyday life unaided – the flood of information got in the way. So knowing every last detail is definitely not something to aspire to.

Information reduction means selection

If it is necessary and desirable to lose data, the next question concerns which data we should lose and which we should retain. Some will imagine that this is a natural choice, with the object we are looking at determining which data is important and which is not. In my opinion, this assumption is simply wrong. It is the observer who decides which information is important to him and which he can disregard. The information he chooses to retain will depend upon his goals.

Of course, the observer cannot get information out of the object that the object does not contain. But the decision as to which information he considers important is down to him – or to the system he feels an allegiance to.

This is particularly true in the field of medicine. What is important is the information about the patient that allows the doctor to make a meaningful diagnosis – and the system of diagnoses depends essentially on what can be treated and how. Medical progress means that the aspects and data that come into play will change over time.

In other words, we cannot know everything, and we must actively reduce the amount of information available so that we can make decisions and act. Information reduction is inevitable and always involves making a choice.

Different selections are possible

Which information is lost and which is retained? The answer to this question determines what we see when we look at an object.

Interpretation der Realität

Various information selections (interpretations) are possible

Because the observer – or the system that he lives in and that moulds and shapes his thinking – decides which information to keep, different selections are possible. Depending on which features we prioritise, different individual cases may be placed in a given group or category and different viewers will thus arrive at different interpretations of the same reality.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 2: The Funnel

Leave a comment
The funnel of information reduction

In my previous article Information reduction 1, I described a chain of information processing from the patient to the flat rate per case (DRG):

This acts as a funnel, reducing the amount of information available at each step.  The extent of the reduction is dramatic. Imagine we have the patient in front of us. One aspect of a comprehensive description of this patient is their red blood cells. There are 24-30 trillion (= 24–30·1012 ) red blood cells in the human body, each with a particular shape and location in the body, and each moving in a particular way at any given time and containing a certain amount of red blood pigment. That is indeed a lot of information. But, of course, we don’t need to know all these details. As a rule, it is sufficient to know whether there is enough red blood pigment (haemoglobin) in the bloodstream. Only if this is not the case (as with anaemia) do we want to know more. Thus, we reduce the information about the patient, selecting only that which is necessary. This is entirely reasonable, even though we lose information in the process.

The funnel, quantified

To quantify how much information reduction takes place, I have cited the number of possible states at each stage of information processing in the above figure. From bottom to top, these are as follows:

  • DRGs (flat rates per case): There are various DRG systems. However, there are always about 1000 different flat rates, i.e. 103 At the level of the flat rate per case, therefore, 103 different states are possible. This is the information that is available at this level.
  • Codes: In Switzerland, the ICD-10 classification system offers 15,000 different codes Let us assume, as an approximation, that each patient has two diagnoses. So we can choose between 15,000 states twice, giving 225,000,000 = 2.25 x
  • 108
  • .
  • Texts: SNOMED, an extensive medical nomenclature, contains about 500,000 (5 x 105) different expressions. Since a medical record contains a great many words, the amount of information here is naturally much more detailed. My estimate of 1015 is definitely on the low side.
  • Perception and reality: I won’t make an estimate. The above example involving red blood cells illustrates the huge amounts of information available in real-world situations.

Read more in Information reduction 3

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 1: Coding

Leave a comment

Two types of coding

In a previous post, I described two fundamentally different types of coding. In the first, the intention is to carry all the information contained in the source over into the encoded version. In the second, on the other hand, we deliberately refrain from doing this. It is the second – the information-losing – type that is of particular interest to us.

When I highlighted this difference in my presentations twenty years ago and the phrase ‘information reduction’ appeared prominently in my slides, my project partners pointed out that this might not go down too well with the audience. After all, everyone wants to win; nobody wants to lose. How can I promote a product for which loss is a quality feature?

Well, sometimes we have to face the fact that the thing we have been trying to avoid at all costs is actually of great value. And that’s certainly the case for information-losing coding.

Medical coding

Our company specialised in the encoding of free-text medical diagnoses. Our program read the diagnoses that doctors write in free text in their patients’ medical records and automatically assigned them a code based upon a standard coding system (ICD-10) with about 15,000 codes (Switzerland, 2019). This sounds like a lot, but the number is small considering the billions of distinguishable diagnoses and diagnostic formulations that occur in the field of medicine (see article). Of course, the individual code cannot contain more information than the standard code is able to discern for the case in question. The full-text diagnoses usually contained more information than this and our task was to automatically extract the relevant parts from the free texts in order to assign the correct code. We were fairly successful in this attempt.

Coding is part of a longer chain

But coding is only one step in a bigger process. Firstly, the information-processing chain extends from codes to flat rates per case (Diagnosis Related Groups = DRGs). Secondly, the free texts to be coded in the medical record are themselves the result of a multi-stage chain of information processing and reduction that has already been performed. Overall, a hospital case involves a chain made up of the following stages from patient examination to flat rate per case:

  • Patient: amount of information contained in the patient.
  • Doctor: amount of information about the patient that the doctor recognises.
  • Medical record: amount of information documented by the doctor.
  • Diagnoses: amount of information contained in the texts regarding the diagnoses.
  • Codes: amount of information contained in the diagnosis codes.
  • Flat rate per case: amount of information contained in the flat rate per case.

The information is reduced at every step, usually quite dramatically. The question is, how does this process work? Can the reduction be automated. And is it a determinate process, or one in which multiple options exist?

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information, Semantics

Two Types of Coding 2

Leave a comment
The two types of coding in set diagrams

I would like to return to the subject of my article Two types of coding 1 and clarify the difference between the two types of coding using set diagrams. I believe this distinction is so important for the field of semanticsand for information theory in general, that it should be generally understood.

Information-preserving coding

The information-preserving type of coding can be represented using the following diagram

Mengendiagramm 1:1-Kodierung

Fig 1: Information-preserving coding (1:1, all codes reachable)

The original form is shown on the left and the encoded form on the right. The red dot on the left could, for example, represent the letter A and the dot on the right the Morse code sequence dot dash. Since this is a 1:1 representation, you can always find your way back from each element on the right to the initial element on the left, i.e. from the dot dash of Morse code to the letter A.

Mengendiagramm 1:1-Kodierung, nicht alle Kodes erreicht

Fig. 2: Information-preserving coding (1:1, not all codes reachable)

Of course, a 1:1 coding system preserves information even if not all codes are used. Since the unused ones can never arise during coding, they play no role at all. For each element of the set depicted on the right that is used for a code, there is exactly one element in the initial form. The code is therefore reversible without loss of information, i.e. decodable, and the original form can be restored without loss for each resulting code.

Mengendarstellung: Informationserhaltende Kodierung (1:n)

Fig. 3: Information-preserving coding (1:n)

With a 1:n system of coding, too, the original form can be reconstructed without loss. An original element can be coded in different ways, but each code has only one original element. There is thus no danger of not getting back to the initial value. Again, it does not matter whether or not all possible codes (elements on the right) are used, since unused codes never need to be reached and therefore do not have to be retranslated.

For all the coding ratios shown so far (1:1 and 1:n), the original information can be fully reconstructed. It doesn’t matter whether we choose a ratio of 1:1 or 1:n, or whether all possible codes are used or some remain free. The only important thing is that each code can only be reached from a single original element. In the language of mathematics, information-preserving codes are injective relations.

Information-reducing coding
Mengendiagramm: Informationsreduzierende Kodierung

Fig. 4: Information-reducing coding (n:1)

In this type of coding, several elements from the initial set point to the same code, i.e. to the same element in the set of resulting codes. This means that the original form can no longer be reconstructed at a later time. The red dot in the figure on the right, for example, represents a code for which there are three different initial forms. The information about the difference between the three dots on the left is lost in the dot on the right and can never be reconstructed. Mathematicians call this a non-injective relation. Coding systems of this type lose information.

Although this type of coding is less ‘clean’, it is nevertheless the one that interests us most, as it typifies many processes in reality.

Information, Semantics

Two Types of Coding 1

Leave a comment
A simple broken bone

In the world of healthcare, medical diagnoses are encoded to improve transparency. This is necessary because they can be formulated in such a wide variety of different ways. For example, a patient may suffer from the following:

– a broken arm
– a distal radius fracture
– a fractura radii loco classico
– a closed extension fracture of the distal radius
– a Raikar’s fracture, left
– a bone fracture of the left distal forearm
– an Fx of the dist. radius l.
– a Colles fracture

Even though they are constructed from different words and abbreviations, all the above expressions can be used to describe the same factual situation, some with more precision than others. And this list is by no means exhaustive. I have been studying such expressions for decades and can assure you without any exaggeration whatsoever that there are billions of different formulations for medical diagnoses, all of them absolutely correct.

Of course, this  huge array of free texts in all variations cannot be processed statistically. The diagnoses are therefore encoded, often using the ICD (International Classification of Diseases) system, which comprises between 15,000 and 80,000 different codes depending on variant. That’s a lot of codes, but much clearer than the billions of possible text formulations it replaces.

Incidentally, the methods used to automate the interpretation of texts so that it can be performed by a computer program are a fascinating subject.

Morse code 

Morse code is used for communication in situations where it’s only possible to send very simple signals. The sender encodes the letters of the alphabet in the form of dots and dashes, which are then transmitted to the recipient, who decodes them by converting them back into letters. An E, for example, becomes a dot and an A becomes a dot followed by a dash. The process of encoding/decoding is perfectly reversible, and the representation unambiguous.

Cryptography

In the field of cryptography, too, we need to be able to translate the code back into its original form. This approach differs from Morse code only in that the translation rule is usually a little more complicated and is known only to a select few. As with Morse code, however, the encrypted form needs to carry the same information as the original.

Information reduction

Morse code and cryptographic codes are both designed so that the receiver can ultimately recreate the original message. The information itself needs to remain unchanged, with only its outer form being altered.

The situation is quite different for ICD coding. Here, we are not dealing with words that are interchangeable on a one-for-one basis such as tibia and shinbone – the ICD is not, and was never intended to be, a reversible coding system. Instead, ICD codes are like drawers in which different diagnoses can be placed, and the process of classification involves deliberately discarding information which is then lost for ever. This is because there is simply too much detail in the diagnoses themselves. For example, a fracture can have the following independent characteristics:

– Name of the bone in question
– Site on the bone
– State of the skin barrier (open, closed)
– Joint involvement (intra-articular, extra-articular)
– Direction of the deformity (flexion, extension, etc.)
– Type of break line (spiral, etc.)
– Number and type of fracture fragments (monoblock, comminuted)
– Cause (trauma, tumour metastasis, fatigue)
– etc.

All these characteristics can be combined, which multiplies the number of possibilities. A statistical breakdown naturally cannot take all combination variants into account, so the diagnostic code covers only a few. In Germany and Switzerland, the ICD can cope with fewer than 20,000 categories for the entire field of medicine. The question of what information the ‘drawers’ can and cannot take into account, is an important topic both for players within the healthcare system and those of us who are interested in information theory and its practical application. Let’s turn now to the coding process.

Two types of coding

I believe that the distinction described above is an important one. On the one hand, we have coding systems that aim to preserve the information itself and change only its form, such as Morse code and cryptographic systems. On the other hand, we have systems such as those for encoding medical diagnosis. These aim to reduce the total amount of information because this is simply too large and needs to be cut down – usually dramatically – for the sake of clarity. Coding to reduce information behaves very differently from coding to preserve information.

This distinction is critical. Mathematical models and scientific theories that apply to information-preserving systems are not suitable for information-reducing ones. In terms of information theory, we are faced with a completely different situation.