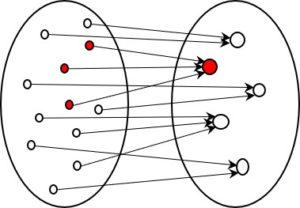
The two types of coding in set diagrams

I would like to return to the subject of my article Two types of coding 1 and clarify the difference between the two types of coding using set diagrams. I believe this distinction is so important for the field of semanticsand for information theory in general, that it should be generally understood.

Information-preserving coding

The information-preserving type of coding can be represented using the following diagram

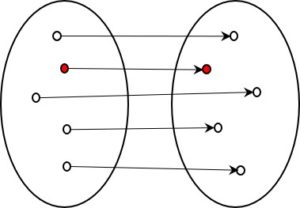
Fig 1: Information-preserving coding (1:1, all codes reachable)

The original form is shown on the left and the encoded form on the right. The red dot on the left could, for example, represent the letter A and the dot on the right the Morse code sequence dot dash. Since this is a 1:1 representation, you can always find your way back from each element on the right to the initial element on the left, i.e. from the dot dash of Morse code to the letter A.

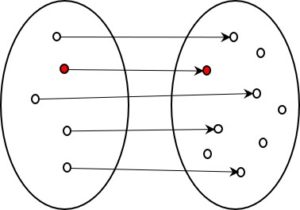
Fig. 2: Information-preserving coding (1:1, not all codes reachable)

Of course, a 1:1 coding system preserves information even if not all codes are used. Since the unused ones can never arise during coding, they play no role at all. For each element of the set depicted on the right that is used for a code, there is exactly one element in the initial form. The code is therefore reversible without loss of information, i.e. decodable, and the original form can be restored without loss for each resulting code.

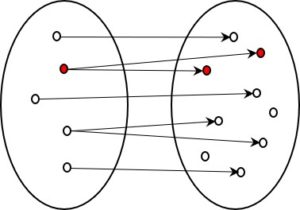
Fig. 3: Information-preserving coding (1:n)

With a 1:n system of coding, too, the original form can be reconstructed without loss. An original element can be coded in different ways, but each code has only one original element. There is thus no danger of not getting back to the initial value. Again, it does not matter whether or not all possible codes (elements on the right) are used, since unused codes never need to be reached and therefore do not have to be retranslated.

For all the coding ratios shown so far (1:1 and 1:n), the original information can be fully reconstructed. It doesn’t matter whether we choose a ratio of 1:1 or 1:n, or whether all possible codes are used or some remain free. The only important thing is that each code can only be reached from a single original element. In the language of mathematics, information-preserving codes are injective relations.

Information-reducing coding

Fig. 4: Information-reducing coding (n:1)

In this type of coding, several elements from the initial set point to the same code, i.e. to the same element in the set of resulting codes. This means that the original form can no longer be reconstructed at a later time. The red dot in the figure on the right, for example, represents a code for which there are three different initial forms. The information about the difference between the three dots on the left is lost in the dot on the right and can never be reconstructed. Mathematicians call this a non-injective relation. Coding systems of this type lose information.

Although this type of coding is less ‘clean’, it is nevertheless the one that interests us most, as it typifies many processes in reality.