Tag Archives: Macro Level

Information

Entropy between Micro- and Macro Level

Leave a comment

Two Levels define Entropy: Micro and Macro

Two levels Define Entropy

The conventional physical definition of entropy characterises it as a difference between two levels: a detail level and an overview level.

Example Coffee Cup

The thermal entropy according to Boltzmann is classic, using the example of an ideal gas. The temperature (1 value) is directly linked to the kinetic energies of the individual gas molecules (1023 values). With certain adjustments, this applies to any material object, e.g. also to a coffee cup:

  1. Thermal macro state: temperature of the liquid in the cup.
  2. Thermal micro state: kinetic energy of all individual molecules in the cup

The values of a) and b) are directly connected. The heat energy of the liquid, which is expressed in the temperature of the coffee, is made up of the kinetic energies of the many (~ 1023) individual molecules in the liquid. The faster the molecules move, the hotter the coffee.

The movement of the individual molecules b) is not constant, however. Rather, the molecules are constantly colliding, changing their speed and therefore their energy. Nevertheless, the total energy after each collision is the same. Because of the energy theorem, the energy of the molecules involved changes with each collision, but the energy of all the molecules involved together remains the same. Even if the coffee cools down slowly or if the liquid is heated from the outside, the interdependence is maintained: The single overall value (temperature) and the many detailed values (movements) are always interdependent.

Example Forest and Trees

The well-known proverb warns us not to see the wood for the trees. This is an helpful picture for the tension between micro and macro level.

Forest: macro level

Trees: micro level

On the micro level we see the details, on the macro level we recognise the big picture. So which view is better? The forest or the trees?

  • Both macro level and micro level are useful – depending on the task
  • Both refer to the same object.
  • Both cannot be discerned at the same time
    -> When you look at the forest, you can’t see the individual trees
    -> If you look at the trees, you miss the forest

We generally believe that it is better to know all the details. But this is a delusion. We always need an overview. Otherwise we would get lost in the details.

So Where is the Entropy?

We can now enumerate all the details of the micro view and thus obtain the information content – e.g. in bits – of the micro state. In the macro state, however, we have a much smaller amount of bits. The difference between the two amounts is the entropy, namely the information that is present in the micro state (trees) but missing in the macro state (forest).

Why isn’t the information content at the micro level the absolute entropy?

The information content at the micro level can be calculated in bits. Does this amount of bits correspond to entropy? If so, the information content at the macro level would simply be a loss of information. The actual information would then be in the micro level of details.

This is the spontaneous expectation that I repeatedly encounter with dialogue partners. They assume that there is an absolute information content, and in their eyes, this is naturally the one with the greatest amount of detail.

A problem with this conception is that the ‘deepest’ micro-level is not clearly defined. The trees are a lower level of information in relation to the forest – but this does not mean that the deepest level of detail has been reached. You can describe the trees in terms of their components – branches, twigs, leaves, roots, trunk, cells, etc. – which is undoubtedly a deeper level than just trees and would contain even more details. But even this level would not be deep enough. We still can go deeper into the details and describe the different cells of the tree, the organelles in the cells, the molecules in the organelles and so on. We would then arrive at the quantum level. But is that the deepest level? Perhaps, but that is not certain. And the further we go into the details, the further we move away from the description of the forest. What interests us is the description of the forest and the lowest level is not necessary for this. The deeper down we search, the further we move away from the description of our object.

→ The deepest micro level is not unequivocally defined!

We can therefore not assign a distinct absolute entropy for our object. Because the micro level can be set at any depth, the entropy, i.e. the quantitative information content at this level, also changes. the deeper, the more information, the higher the entropy.

Is There an Absolute Macro Level?

Like the micro level, the highest information level, e.g., of a forest, is not clearly defined as well.

Is this macro level the image that represents an optical view of the forest as seen by a bird flying over it? Or is it the representation of the forest on a map? At what scale? 1:25,000 or 1:100,000? Obviously the amount of information of the respective macro state changes depending on the view.

What are we interested in when we describe the forest? The paths through the forest? The tree species? Are there deer and rabbits? How healthy is the forest?

In other words, the forest, like any object, can be described in very different ways.

There is no clear, absolute macro level. A different macro representation applies depending on the situation and requirements.

The Relativity of Micro and Macro Levels

At each level, there is a quantitative amount of information, the deeper the richer, the higher the clearer. It would be a mistake, however, to label a specific level with its amount of information as the lowest or the highest. Both are arbitrary. They are not laid by the object, but by the observer.

The Difference is the Information

As soon as we accept that both micro and macro levels can be set arbitrarily, we approach a more real concept of information. It suddenly makes sense to speak of a difference. The difference between the two levels define the span of knowledge.

The information that I can gain is the information that I lack at the macro level, but which I find at the micro level. The difference between the two levels in terms of their entropy is the information that I can gain in this process.

Conversely, if I have the details of the micro level in front of me and want to gain an overview, I have to simplify this information of the micro level and reduce its number of bits. This reduction is the entropy, i.e. the information that I consciously relinquish.

The Information Paradox

If I want to extract the information that interests me from a jumble of details, i.e. if I want to get from a detailed description to useful information, then I have to ignore a lot of information at the micro level. I have to lose information in order to get the information I want. This paradox underlies every analytical process.

Information is Relative and Dynamic

What I am proposing is a relative concept of information. This does not correspond to the expectations of most people who have a static idea of the world. The world, however, is fundamentally dynamic. We live in this world – like all other living beings – as information-processing entities. The processing of information is an everyday process for all of us, for all biological entities, from plants to animals to humans.

The processing of information is an existential process for all living beings. This process always has a before and an after. Depending on this, we gain information when we analyse something in detail. And if we want to gain an overview or make a decision (!), then we have to simplify information. So we go from a macro-description to a micro-description and vice versa. Information is a dynamic quantity.

Entropy is the information that is missing at the macro level but can be found at the micro level.

And vice versa: entropy is the information that is present at the micro level but – to gain an overview – is ignored at the macro level.

Objects and their Micro and Macro Level

We can assume that a certain object can be described at different levels. According to current scientific findings, it is uncertain whether a deepest level of description can be found, but this is ultimately irrelevant to our information theory considerations. In the same way, it does not make sense to speak of a highest macro level. The macro levels depend on the task at hand.

What is relevant, however, is the distance, i.e. the information that can be gained in the macro state when deeper details are integrated into the view, or when they are discarded for the sake of a better overview. In both cases, there is a difference between two levels of description.

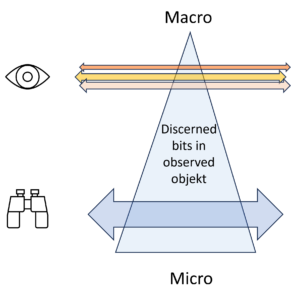
The illustration above visualises the number of detected bits in an object. At the top of the macro level, there are few, at the bottom of the micro level there are many. The object remains the same whether many or few details are taken into account and recognised.

The macro view brings a few bits, but their selection is not determined by the object alone, but rather by the interest behind the view of the observer.

The number of bits, i.e. the entropy, decreases from bottom to top. The heigth of the level, however, is not a property of the object of observation, but a property of the observation itself. Depending on my intention, I see it  the observed object differently, sometimes detailed and unclear, another time clear and simplified, i.e. sometimes with a lot of entropy and another time with less entropy.

Information acquisition is the dynamic process that either:

a) gains more details: Macro → Micro
b) gains more overview: Micro → Macro

In both cases, the amount of information (entropy as the amount of bits) is changed. The bits gained or lost correspond to the difference in entropy between the micro and macro levels.

When I examine the object, it reveals more or less information depending on how I look at it. Information is always relative to prior knowledge and must be understood dynamically.

Translation: Juan Utzinger

 

Information, Logic

What is Entropy?

Leave a comment

Definition of Entropy

The term entropy is often avoided because it contains a certain complexity. The phenomenon entropy, however, is constitutive for everything that is going on in our lives. A closer look is worth the effort.

Entropy is a measure of information and it is defined as:

Entropy is the information
– known at micro,
– but unknown at macro level.

The challenge of this definition is:

  1. to understand what is meant by the micro and macro states and
  2. ​to understand why entropy is a difference.

​What is Meant by Micro and Macro Level?

The micro level contains the details (i.e. a lot of information), the macro level contains the overview (i.e. less, but more targeted information). The distance between the two levels can be very small (as with the bit, where the microlevel knows just two pieces of information: on or off) or huge, as with the temperature (macrolevel) of the coffee in a coffee cup, where the kinetic energies of the many molecules (microlevel) determine the temperature of the coffee. The number of molecules in the cup is really large (in the order of Avogadro’s number 1023) and the entropy of the coffee in the cup is correspondingly high.

Entropy is thus defined by the two states and their difference. However, states and difference are neither constant nor absolute, but a question of observation, therefore relative.

Let’s take a closer look at what this relativity means for the macro level.

​​What is the Relevant Macro Level?

In many fields like biology, psychology, sociology, etc. and in art, it is obious to me as a layman, that the notion of the two levels is applicable to these fields, too. They are, of course, more complex than a coffee cup, so that the simple thermodynamic relationship between micro and macro becomes more complex.

In particular, it is conceivable to have a mixture of several macro-states occurring simultaneously. For example, an individual (micro level), may belong to the macro groups of the Swiss, the computer scientists, the older men, the contemporaries of 2024, etc – all at the same time. Therefore, applying entropy reasoning to sociology is not as straightforward as the simple examples like Boltzmann’s coffee cup, Salm’s lost key, or a basic bit might suggest.

Entropy as a Difference

Micro and macro level of an object both have their own entropy. But what really matters ist the difference of the two entropies. The bigger the difference, the more is unknown on the macro level about the micro level.

The difference between micro and macro level says a lot about the way we perceive information. In simple words: when we learn something new, information is moved from micro to macro state.

The conventional definition of entropy states that it represents the information present in the micro but absent in the macro state. This definition of entropy via the two states means that the much more detailed microstate is not primarily visible to the macrostate. This is exactly what Niklas Luhmann meant when he spoke of intransparency1.

When an observer interprets the incoming signals (micro level) at his macro level, he attempts to gain order or transparency from an intransparent multiplicity. How he does this is an exciting story. Order – a clear and simple macro state – is the aim in many places: In my home, when I tidy up the kitchen or the office. In every biological body, when it tries to maintain constant form and chemical ratios. In society, when unrest and tensions are a threat, in the brain, when the countless signals from the sensory organs have to be integrated in order to recognise the environment in a meaningful interpretation, and so on. Interpretation is always a simplification, a reduction of information = entropy reduction.

Entropy and the Observer

An essential point is that the information reduction from micro to macro state is always carried out by an active interpreter and guided by his interest.

The human body, e.g., controls the activity of the thyroid hormones via several control stages, which guarantee that the resulting state (macro state) of the activity of body and mind remains within an adequate range even in case of external disturbances.

The game of building up a macro state (order) out of the many details of a micro state is to be found everywhere in biology, sociology and in our everyday live.

There is – in all these examples – an active control system that steers the reduction of entropy in terms of the bigger picture. This control in the interpretation of the microstate is a remarkable phenomenon. Always when transparency is wanted, an information rich micro state must be simplified to a macro state with less details.

Entropy can then be measured as the difference in information from the micro to the macro level. When the observer interprets signals from the micro level, he creates transparency from intransparency.

Entropy, Re-Entry and Oscillation

We can now have a look at the entropy relations in the re-entry phenomenon as described by Spencer-Brown2. Because the re-entry ‘re-enters’ the same distinction that it has just identified, there is hardly any information difference between before and after the re-entry and therefore hardly any difference between its micro and macro state. After all, it is the same distinction.

However, there is a before and an after, which may oscillate, whereby its value becomes imaginary (this is precisely described in chapter 11 of Spencer-Browns book ‘Laws of Form’)2. Re-entries are very common in thinking and in complex fields like biology or sociology when actions and their consequences meet their own causes. These loops or re-entries are exciting, both in thought processes and in societal analysis.

The re-entries lead to loops in the interpretation process and in many situations these loops can have puzzling logical effects (see paradoxes1 sand paradoxes2 ). In chapter 11 of ‘Laws of Form’2, Spencer-Brown describes the mathematical and logical effects around the re-entry in details. In particular, he develops how logical oscillations occur due to the re-entry.

Entropy comes into play whenever descriptions of the same object occur simultaneously at different levels of detail, i.e. whenever an actor (e.g. a brain or the kitchen cleaner) wants to create order by organising an information-rich and intransparent microstate in such a way that a much simpler and easier to read macrostate develops.

We could say that the observer actively creates a new macro state from the micro state. However, the micro-state remains and still has the same amount of entropy as before. Only the macro state has less. When I comb my hair, all the hairs are still there, even if they are arranged differently. A macro state is created, but the information can still be described at the detailed micro level of all the hairs, albeit slightly altered in the arrangement on the macro level.
Re-entry – on the other hand – is a powerful logical pattern. For me, both re-entry and entropy complement each other in the description of reality. Distinction and re-entry are very elementary. Entropy, on the other hand, always arises when several things come together and their arrangement is altered or differentely interpreted.

See also: Five preconceptions about entropy

Translation: Juan Utzinger

1 Niklas Luhmann, Die Kontrolle von Intransparenz, hrsg. von Dirk Baecker, Berlin: Suhrkamp 2017, S. 96-120

2 Georg Spencer Brown , Laws of Form, London 1969, (Bohmmeier, Leipzig, 2011)

Information

Information Reduction 5: The Classic Glass of Water

Leave a comment
Information reduction in thermodynamics

A very specific example of information reduction can be found in the field of thermodynamics. What makes this example so special is its simplicity. It clearly illustrates the basic structure of information reduction without the complexity found in other examples, such as those from biology. And it’s a subject many of us will already be familiar with from our physics lessons at school.

What is temperature?

A glass of water contains a huge amount of water molecules, all moving at different speeds and in different directions. These continuously collide with other water molecules, and their speed and direction of travel changes with each impact. In other words, the glass of water is a typical example of a real object that contains more information than an external observer can possibly deal with.

That’s the situation for the water molecules. So what is the temperature of the water in the glass?

As Ludwig Boltzmann was able to demonstrate, temperature is simply the result of the movement of the many individual water molecules in the glass. The faster they move, the more energy they have and the higher is the temperature of the water As Ludwig Boltzmann explained, the temperature of the water in the glass can be calculated statistically from the kinetic energy of the many molecules. Billions of molecules with their constantly changing motion produce exactly one temperature. Thus, a large amount of information is converted into a single fact.

The micro level and the macro level

It’s worth noting that the concept of temperature cannot be applied to individual molecules. At this level, there is only the movement of many single molecules, which changes with each impact. The kinetic energy of the molecules depends on their speed and thus changes with each impact.

Although the motion of the water molecules is constantly changing at the micro level, the temperature at the macro level of the glass of water remains comparatively constant. And, in the event that it does change, for example because heat is given off from the water at the walls of the glass, there are formulas that can be used to calculate the movement of the heat and thus the change in temperature. These formulas remain at the macro level, i.e. they do not involve the many complicated impacts and movements of the water molecules.

The temperature profile can thus be described and calculated entirely at the macro level without needing to know the details of the micro level and its vast number of water molecules. Although the temperature (macro level) is defined entirely and exclusively by the movement of the molecules (micro level), we don’t need to know the details to predict its value. The details of the micro level seem to disappear at the macro level. This is a typical case of information reduction.

In the next post I’ll make some precisions concerning the waterglass.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford