Category Archives: Information

Information

Entropy between Micro- and Macro Level

Leave a comment

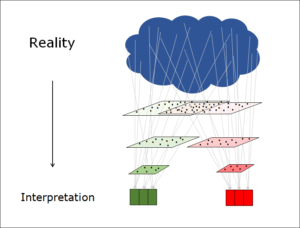
Two Levels define Entropy: Micro and Macro

Two levels Define Entropy

The conventional physical definition of entropy characterises it as a difference between two levels: a detail level and an overview level.

Example Coffee Cup

The thermal entropy according to Boltzmann is classic, using the example of an ideal gas. The temperature (1 value) is directly linked to the kinetic energies of the individual gas molecules (1023 values). With certain adjustments, this applies to any material object, e.g. also to a coffee cup:

  1. Thermal macro state: temperature of the liquid in the cup.
  2. Thermal micro state: kinetic energy of all individual molecules in the cup

The values of a) and b) are directly connected. The heat energy of the liquid, which is expressed in the temperature of the coffee, is made up of the kinetic energies of the many (~ 1023) individual molecules in the liquid. The faster the molecules move, the hotter the coffee.

The movement of the individual molecules b) is not constant, however. Rather, the molecules are constantly colliding, changing their speed and therefore their energy. Nevertheless, the total energy after each collision is the same. Because of the energy theorem, the energy of the molecules involved changes with each collision, but the energy of all the molecules involved together remains the same. Even if the coffee cools down slowly or if the liquid is heated from the outside, the interdependence is maintained: The single overall value (temperature) and the many detailed values (movements) are always interdependent.

Example Forest and Trees

The well-known proverb warns us not to see the wood for the trees. This is an helpful picture for the tension between micro and macro level.

Forest: macro level

Trees: micro level

On the micro level we see the details, on the macro level we recognise the big picture. So which view is better? The forest or the trees?

  • Both macro level and micro level are useful – depending on the task
  • Both refer to the same object.
  • Both cannot be discerned at the same time
    -> When you look at the forest, you can’t see the individual trees
    -> If you look at the trees, you miss the forest

We generally believe that it is better to know all the details. But this is a delusion. We always need an overview. Otherwise we would get lost in the details.

So Where is the Entropy?

We can now enumerate all the details of the micro view and thus obtain the information content – e.g. in bits – of the micro state. In the macro state, however, we have a much smaller amount of bits. The difference between the two amounts is the entropy, namely the information that is present in the micro state (trees) but missing in the macro state (forest).

Why isn’t the information content at the micro level the absolute entropy?

The information content at the micro level can be calculated in bits. Does this amount of bits correspond to entropy? If so, the information content at the macro level would simply be a loss of information. The actual information would then be in the micro level of details.

This is the spontaneous expectation that I repeatedly encounter with dialogue partners. They assume that there is an absolute information content, and in their eyes, this is naturally the one with the greatest amount of detail.

A problem with this conception is that the ‘deepest’ micro-level is not clearly defined. The trees are a lower level of information in relation to the forest – but this does not mean that the deepest level of detail has been reached. You can describe the trees in terms of their components – branches, twigs, leaves, roots, trunk, cells, etc. – which is undoubtedly a deeper level than just trees and would contain even more details. But even this level would not be deep enough. We still can go deeper into the details and describe the different cells of the tree, the organelles in the cells, the molecules in the organelles and so on. We would then arrive at the quantum level. But is that the deepest level? Perhaps, but that is not certain. And the further we go into the details, the further we move away from the description of the forest. What interests us is the description of the forest and the lowest level is not necessary for this. The deeper down we search, the further we move away from the description of our object.

→ The deepest micro level is not unequivocally defined!

We can therefore not assign a distinct absolute entropy for our object. Because the micro level can be set at any depth, the entropy, i.e. the quantitative information content at this level, also changes. the deeper, the more information, the higher the entropy.

Is There an Absolute Macro Level?

Like the micro level, the highest information level, e.g., of a forest, is not clearly defined as well.

Is this macro level the image that represents an optical view of the forest as seen by a bird flying over it? Or is it the representation of the forest on a map? At what scale? 1:25,000 or 1:100,000? Obviously the amount of information of the respective macro state changes depending on the view.

What are we interested in when we describe the forest? The paths through the forest? The tree species? Are there deer and rabbits? How healthy is the forest?

In other words, the forest, like any object, can be described in very different ways.

There is no clear, absolute macro level. A different macro representation applies depending on the situation and requirements.

The Relativity of Micro and Macro Levels

At each level, there is a quantitative amount of information, the deeper the richer, the higher the clearer. It would be a mistake, however, to label a specific level with its amount of information as the lowest or the highest. Both are arbitrary. They are not laid by the object, but by the observer.

The Difference is the Information

As soon as we accept that both micro and macro levels can be set arbitrarily, we approach a more real concept of information. It suddenly makes sense to speak of a difference. The difference between the two levels define the span of knowledge.

The information that I can gain is the information that I lack at the macro level, but which I find at the micro level. The difference between the two levels in terms of their entropy is the information that I can gain in this process.

Conversely, if I have the details of the micro level in front of me and want to gain an overview, I have to simplify this information of the micro level and reduce its number of bits. This reduction is the entropy, i.e. the information that I consciously relinquish.

The Information Paradox

If I want to extract the information that interests me from a jumble of details, i.e. if I want to get from a detailed description to useful information, then I have to ignore a lot of information at the micro level. I have to lose information in order to get the information I want. This paradox underlies every analytical process.

Information is Relative and Dynamic

What I am proposing is a relative concept of information. This does not correspond to the expectations of most people who have a static idea of the world. The world, however, is fundamentally dynamic. We live in this world – like all other living beings – as information-processing entities. The processing of information is an everyday process for all of us, for all biological entities, from plants to animals to humans.

The processing of information is an existential process for all living beings. This process always has a before and an after. Depending on this, we gain information when we analyse something in detail. And if we want to gain an overview or make a decision (!), then we have to simplify information. So we go from a macro-description to a micro-description and vice versa. Information is a dynamic quantity.

Entropy is the information that is missing at the macro level but can be found at the micro level.

And vice versa: entropy is the information that is present at the micro level but – to gain an overview – is ignored at the macro level.

Objects and their Micro and Macro Level

We can assume that a certain object can be described at different levels. According to current scientific findings, it is uncertain whether a deepest level of description can be found, but this is ultimately irrelevant to our information theory considerations. In the same way, it does not make sense to speak of a highest macro level. The macro levels depend on the task at hand.

What is relevant, however, is the distance, i.e. the information that can be gained in the macro state when deeper details are integrated into the view, or when they are discarded for the sake of a better overview. In both cases, there is a difference between two levels of description.

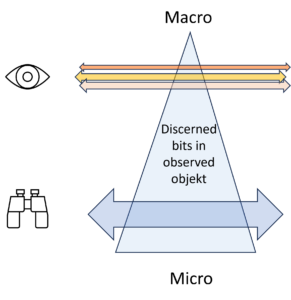
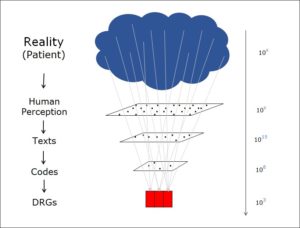
The illustration above visualises the number of detected bits in an object. At the top of the macro level, there are few, at the bottom of the micro level there are many. The object remains the same whether many or few details are taken into account and recognised.

The macro view brings a few bits, but their selection is not determined by the object alone, but rather by the interest behind the view of the observer.

The number of bits, i.e. the entropy, decreases from bottom to top. The heigth of the level, however, is not a property of the object of observation, but a property of the observation itself. Depending on my intention, I see it  the observed object differently, sometimes detailed and unclear, another time clear and simplified, i.e. sometimes with a lot of entropy and another time with less entropy.

Information acquisition is the dynamic process that either:

a) gains more details: Macro → Micro
b) gains more overview: Micro → Macro

In both cases, the amount of information (entropy as the amount of bits) is changed. The bits gained or lost correspond to the difference in entropy between the micro and macro levels.

When I examine the object, it reveals more or less information depending on how I look at it. Information is always relative to prior knowledge and must be understood dynamically.

Translation: Juan Utzinger

 

Information

Entropy and Information

Leave a comment

Entropy and Information

The term entropy is often avoided because it contains a certain complexity that cannot be argued away.
But when we talk about information, we also have to talk about entropy. Because entropy is the measure of the amount of information. We cannot understand what information is without understanding what entropy is.

Information is Always Relative

We believe that we can pack information, just as we store bits in a storage medium. Bits are there objectively available, like little beads in a chain that can say yes or no. For us, this is information. But this image is deceptive. We have become so accustomed to this picture that we can’t imagine otherwise.

Of course, the bit-spherules do not say ‘yes’ or ‘no’, nor 0 or 1, nor TRUE or FALSE, of anything else in particular. Bits have no meaning at all, unless you have defined this meaning from the outside. Then they can perfectly say 1, TRUE, ‘I’m coming to dinner tonight’ or something else, but only together with their environment, their context.

This consideration makes it clear that information is relative. The bit only acquires its meaning from its placement. Depending on its context, it means 0 or 1, ‘true’ or ‘false’, etc. The bit is set in its place, but its meaning only comes from its place.

The place and its context, must therefore be taken into account so that it becomes clear what the bit is supposed to mean. And of course, the meaning is relative, i.e. the same bit can have a completely different meaning in a different context, a different place.

This relativity characterises not only the bit, but every type of information. Every piece of information only acquires its meaning through the context in which it is placed. It is therefore relative. Bits are just signals. What they mean only becomes clear when you interpret the signals from your perspective, when you look at it from your context.

Only then does the signal take on a meaning for you. This meaning is not absolute, because whenever we try to isolate it from its context, it will be reduced to a signal mere signal.  The meaning can only be found relative in the interaction between your expectation, the context and the position of the bit. There it is a switch, which can be set to ON or OFF. However, ON and OFF only inform about the position of the switch. Everything else is in the surroundings.

Definition of Entropy

Considering how important information and information technologies are today, it is astonishing how little is known about the scientific definition of entropy, i.e. information:

Entropy is a measure of the information that is 
– known in the micro 
– but unknown in the macro level.

Entropy is therefore closely related to information at the micro and macro levels and can be seen as the ‘distance’ or difference between the information at the two information levels.

Micro and Macro Level Define Information

What is meant by this gap between the micro and macro levels?  –  When we look at an object, the micro level contains the details (i.e. a lot of information), and the macro level contains the overview (i.e. less, but more targeted information).

The distance between the two levels can be very small (as with the bit, where the microlevel knows just two pieces of information: on or off) or huge, as with the temperature (macrolevel) in the coffee cup, for example, where the kinetic energies of the many molecules (microlevel) determine the temperature of the coffee. The number of molecules in this case lies in the order of Avogadro’s number 1023, i.e. quite high, and the entropy of the coffee in the cup is correspondingly high.
On the other hand, when the span between micro and macro level becomes very narrow, the information (entropy) will be small and comes very close to the size of a bit (info content = 1). However, it always depends on the relation between micro and macro level. This relation – i.e. what is known in the micro level but not in the macro level – defines the information that you receive, namely the information that a closer look at the details reveals.

The Complexity of the Macro Level

A state on the macro level always contains less information than on the micro state. The macro state is not complete, it never can contain all information one could possibly get by a closer look, but in most cases it is a well targeted and intended simplification of the information at the micro level.

This means that the same micro-state can supply different macro-states. For example: a certain individual (micro level), can belong to the collective macro groups of Swiss inhabitants, computer scientists, older men, contemporaries of the year 2024, etc., all at the same time.

The possibility of simultaneously drawing out several macro-states from different micro-states is characteristic of the complexity of micro- and macro-states and thus also of entropy.

If we transfer the entropy consideration of thermodynamics to more complex networks, we must deal with their higher complexity, but the ideas of micro and macro state remain and help us to understand what is going on when information is gained and processed.

Translation: Juan Utzinger

Continued in Entropy, Part 2

See also:
– Paradoxes and Logic, Part 2
– Georg Spencer-Brown’s Distinction and the Bit
–  What is Entropy?
– Five Preconceptions about Entropy

Information, Logic

What is Entropy?

Leave a comment

Definition of Entropy

The term entropy is often avoided because it contains a certain complexity. The phenomenon entropy, however, is constitutive for everything that is going on in our lives. A closer look is worth the effort.

Entropy is a measure of information and it is defined as:

Entropy is the information
– known at micro,
– but unknown at macro level.

The challenge of this definition is:

  1. to understand what is meant by the micro and macro states and
  2. ​to understand why entropy is a difference.

​What is Meant by Micro and Macro Level?

The micro level contains the details (i.e. a lot of information), the macro level contains the overview (i.e. less, but more targeted information). The distance between the two levels can be very small (as with the bit, where the microlevel knows just two pieces of information: on or off) or huge, as with the temperature (macrolevel) of the coffee in a coffee cup, where the kinetic energies of the many molecules (microlevel) determine the temperature of the coffee. The number of molecules in the cup is really large (in the order of Avogadro’s number 1023) and the entropy of the coffee in the cup is correspondingly high.

Entropy is thus defined by the two states and their difference. However, states and difference are neither constant nor absolute, but a question of observation, therefore relative.

Let’s take a closer look at what this relativity means for the macro level.

​​What is the Relevant Macro Level?

In many fields like biology, psychology, sociology, etc. and in art, it is obious to me as a layman, that the notion of the two levels is applicable to these fields, too. They are, of course, more complex than a coffee cup, so that the simple thermodynamic relationship between micro and macro becomes more complex.

In particular, it is conceivable to have a mixture of several macro-states occurring simultaneously. For example, an individual (micro level), may belong to the macro groups of the Swiss, the computer scientists, the older men, the contemporaries of 2024, etc – all at the same time. Therefore, applying entropy reasoning to sociology is not as straightforward as the simple examples like Boltzmann’s coffee cup, Salm’s lost key, or a basic bit might suggest.

Entropy as a Difference

Micro and macro level of an object both have their own entropy. But what really matters ist the difference of the two entropies. The bigger the difference, the more is unknown on the macro level about the micro level.

The difference between micro and macro level says a lot about the way we perceive information. In simple words: when we learn something new, information is moved from micro to macro state.

The conventional definition of entropy states that it represents the information present in the micro but absent in the macro state. This definition of entropy via the two states means that the much more detailed microstate is not primarily visible to the macrostate. This is exactly what Niklas Luhmann meant when he spoke of intransparency1.

When an observer interprets the incoming signals (micro level) at his macro level, he attempts to gain order or transparency from an intransparent multiplicity. How he does this is an exciting story. Order – a clear and simple macro state – is the aim in many places: In my home, when I tidy up the kitchen or the office. In every biological body, when it tries to maintain constant form and chemical ratios. In society, when unrest and tensions are a threat, in the brain, when the countless signals from the sensory organs have to be integrated in order to recognise the environment in a meaningful interpretation, and so on. Interpretation is always a simplification, a reduction of information = entropy reduction.

Entropy and the Observer

An essential point is that the information reduction from micro to macro state is always carried out by an active interpreter and guided by his interest.

The human body, e.g., controls the activity of the thyroid hormones via several control stages, which guarantee that the resulting state (macro state) of the activity of body and mind remains within an adequate range even in case of external disturbances.

The game of building up a macro state (order) out of the many details of a micro state is to be found everywhere in biology, sociology and in our everyday live.

There is – in all these examples – an active control system that steers the reduction of entropy in terms of the bigger picture. This control in the interpretation of the microstate is a remarkable phenomenon. Always when transparency is wanted, an information rich micro state must be simplified to a macro state with less details.

Entropy can then be measured as the difference in information from the micro to the macro level. When the observer interprets signals from the micro level, he creates transparency from intransparency.

Entropy, Re-Entry and Oscillation

We can now have a look at the entropy relations in the re-entry phenomenon as described by Spencer-Brown2. Because the re-entry ‘re-enters’ the same distinction that it has just identified, there is hardly any information difference between before and after the re-entry and therefore hardly any difference between its micro and macro state. After all, it is the same distinction.

However, there is a before and an after, which may oscillate, whereby its value becomes imaginary (this is precisely described in chapter 11 of Spencer-Browns book ‘Laws of Form’)2. Re-entries are very common in thinking and in complex fields like biology or sociology when actions and their consequences meet their own causes. These loops or re-entries are exciting, both in thought processes and in societal analysis.

The re-entries lead to loops in the interpretation process and in many situations these loops can have puzzling logical effects (see paradoxes1 sand paradoxes2 ). In chapter 11 of ‘Laws of Form’2, Spencer-Brown describes the mathematical and logical effects around the re-entry in details. In particular, he develops how logical oscillations occur due to the re-entry.

Entropy comes into play whenever descriptions of the same object occur simultaneously at different levels of detail, i.e. whenever an actor (e.g. a brain or the kitchen cleaner) wants to create order by organising an information-rich and intransparent microstate in such a way that a much simpler and easier to read macrostate develops.

We could say that the observer actively creates a new macro state from the micro state. However, the micro-state remains and still has the same amount of entropy as before. Only the macro state has less. When I comb my hair, all the hairs are still there, even if they are arranged differently. A macro state is created, but the information can still be described at the detailed micro level of all the hairs, albeit slightly altered in the arrangement on the macro level.
Re-entry – on the other hand – is a powerful logical pattern. For me, both re-entry and entropy complement each other in the description of reality. Distinction and re-entry are very elementary. Entropy, on the other hand, always arises when several things come together and their arrangement is altered or differentely interpreted.

See also:
Five preconceptions about entropy
Category: Entropy

Translation: Juan Utzinger

1 Niklas Luhmann, Die Kontrolle von Intransparenz, hrsg. von Dirk Baecker, Berlin: Suhrkamp 2017, S. 96-120

2 Georg Spencer Brown , Laws of Form, London 1969, (Bohmmeier, Leipzig, 2011)

Information, Logic

Georg Spencer-Browns Distinction and the Bit

Leave a comment

continues paradoxes and logic (part 2)

History

Before we Georg Spencer-Brown’s (GSB’s) distinction as basic element for logic, physics, biology and philosophy, it is helpful to compare it with another, much better-known basic form, namely the bit. This allows us to better understand the nature of GSB’s distinction and the revolutionary nature of his innovation.

Bits and GSB forms can both be regarded as basic building blocks for information processing. Software structures are technically based on bits, but the forms of GSB (‘draw a distinction’) are just as simple, fundamental and astonishingly similar. Nevertheless, there are characteristic differences.

 Fig. 1: Form and bit show similarities and differences

Both the bit and the Spencer-Brown form were found in the early phase of computer science, so they are relatively new ideas. The bit was described by C. A. Shannon in 1948, the distinction by Georg Spencer-Brown (GSB) in his book ‘Laws of Form’ in 1969, only about 20 years later. 1969 fell in the heyday of the hippie movement and GSB was warmly welcomed Esalen, an intellectual hotspot and starting point of this movement.  This may have put him – on the other hand – in a bad light and hindered the established scientific community to look closer into his ideas. While the handy bit vivified California’s nascent high-tech information movement, Spencer-Brown’s mathematical and logical revolution was rather ignored by the scientific community. It’s time to overcome this disparity.

Similarities between Distinction and Bit

Both the form and the bit refer to information. Both are elementary abstractions and can therefore be seen as basic building blocks of information.

This similarity reveals itself in the fact that both denote a single action step – albeit a different one – and both assign a maximally reduced number of results to this action, exactly two.

Table 1: Both Bit and Distinction each contain
one action and two possible results (outcomes)

Exactly one Action, Exactly Two Potential Results

The action of the distinction is – as name says – the distinction, and the action of the bit is the selection. Both actions can be seen as information actions and are as such fundamental, i.e. not further reducible. The bit does not contain further bits, the distinction does not contain further distinctions. Of course, there are other bits in the vicinity of the bit and other distinctions in the vicinity of a distinction. However, both actions are to be seen as fundamental information actions. Their fundamentality is emphasised by the smallest possible number of results, namely two. The number of results cannot be smaller, because a distinction of 1 is not a distinction and a selection of 1 is not a selection. Both are only possible if there are two potential results.

Both distinction and bit are thus indivisible acts of information of radical, non-increasable simplicity.

Nevertheless, they are not the same and are not interchangeable. They complement each other.

While the bit has seen a technical boom since 1948, its prerequisite, the distinction, has remained unmentioned in the background. It is all the more worthwhile to bring it to the foreground today and shed new light on what links mathematics, logic, the natural sciences and the humanities.

Differences

Information Content and Shannons Bit

Both form and bit refer to information. In physics, the quantitative content of information is referred to as entropy.

At first glance, the information content when a bit is set or a distinction is made appears to be the same in both cases, namely the information that distinguishes between two states. This is clearly the case with a bit. As Shannon has shown, its information content is log2(2) = 1. Shannon called this dimensionless value 1 bit. The bit therefore contains – not surprisingly – the information of one bit, as defined by Shannon.

The Bit and its Entropy

The bit measures nothing other than entropy. The term entropy originally came from thermodynamics and was used to calculate the behaviour of heat machines. Entropy is in thermodynamics the partner term of energy, but it applies – like the term energy – to all fields of physics, not just to thermodynamics.

What is Entropy ?

Entropy is a measure for the information content. If I do not know something and then discover it, information flows. In a bit, there are – before I know which one is true – two states possible, the two states of the bit . When I find out which of the two states is true, I receive a small basic portion of information with the quantitative value of 1 bit.

One bit decides about two results. If more than two states are possible, the number of bits increases logarithmically with the number of possible states; so it takes three binary elections (bits) to find the correct choice out of 8 possibilities. The number of choices (bits) behaves logarithmically to the number of possible choices, as the example shows.

Dual choice = 1 Bit = log2(2).
Quadruple choice= 2 Bit = log2(4)
Octuple choice = 3 Bit = log2(8)

The information content of a single bit is always the information content of a single binary choice, i.e. log2(2) = 1.

The bit as a physical quantity is dimensionless, i.e. a pure number. This suits because the information about the choice is neutral, and not a length, a weight, an energy or a temperature. The bit serves well as the technical unit of quantitative information content. What is different with the other basic unit of information, the form of Spencer-Brown?

The Information Content of the Form

The information content of the bit is exactly 1 if the two outcomes of the selection have exactly the same probability. As soon as one of the two states is less probable, its choice reveals more information. When it is selected despite its lower prior probability, this makes more of a difference and reveals more information to us. The less probable its choice is, the greater the information will be, if it is selected. The classic bit is a special case in this regard: the probability of its two states is equal by definition and the information content of the choice is exactely 1.

This is entirely different with Spencer-Brown’s form of distinction. The decisive factor lies in the ‘unmarked space’. The distinction distinguishes something from the rest and marks it. The rest, i.e. everything else, remains unmarked. Spencer-Brown calls it the ‘unmarked space’.

We can and must now assume that the remainder, the unmarked, is much greater, and the probability of its occurrence is much higher than the probability that the marked will occur. The information content of the mark, i.e. of the drawing the distinction, is therefore usually greater than 1.

Of course, the distinction is about the marked and the marked is what interests us. That is why the information content of the distinction is calculated based on the marked and not the unmarked.

How large is the space of the unmarked? We would do well to assume that it is infinite. I can never know what I don’t know.

The difference in information content, measured as entropy, is the first difference we can see between bit and distinction. The information content of the bit, i.e. its entropy, is exactly 1. In the case of distiction, it depends on how large the unmarked space is, but it is always larger than the marked space and the entropy of the distinction is therefore always greater than 1.

Closeness and Openness

Fig. 1 above shows the most important difference between distinction and bit, namely their external boundaries. These are clearly defined in the case of the bit.

The meaning in the bit

The bit contains two states, one of which is activated, the other not. Apart from these two states, nothing can be seen in the bit and all other information is outside the bit. Not even the meanings of the two states are defined. They can mean 0 and 1, true and false, positive and negative or any other pair that is mutually exclusive. The bit itself does not contain these meanings, only the information as to which of the two predefined states was selected. The meaning of the two states is regulated outside the bit and assigned from outside. This neutrality of the bit is its strength. It can take on any meaning and can therefore be used anywhere where information is technically processed.

The meaning in the distinction

The situation is completely different with distinction. Here the meaning is marked. To do this, the inside of the distinction is distinguished from the outside. The outside, however, is open and there is nothing that does not belong to it. The ‘unmarked space’, in principle, is infinite. A boundary is defined, but it is the distinction itself. That is why the distinction cannot really separate itself from the outside, unlike the bit. In other words: The bit is closed, the distinction is not.

Differences between Distinction and Bit
​

There are two essential differences between distionction and bit.

Table 2: Differences between Distinction (Form) and Bit

​Consequences

The two difference between distinction and bit have some interesting consequences.

Example NLP (Natural Language Processing)

The bit, due to its defined and simple entropy and its close borders, has the technological advantage of simple usability, which we exploit in the software industry. Distinctions, on the other hand, are more realistic due to their openness. For our specific task of interpreting medical texts, we therefore came across the need to introduce openness into the bit world of technical software through certain principles: The keywords here are

  1. Introduction of an acting subject that evaluates the input according to its own internal rules,
  2. Working with changing ontologies and classifications,
  3. Turning away from the classical, i.e. static and montonic logic and turning towards a non-monotonic logic,
  4. Integration of time as a logical element (not just as a variable).

Translation: Juan Utzinger

 

Information, Logic

Paradoxes and Logic (Part 2)

Leave a comment

continues Paradoxes and Logic (part 1)

“Draw a Distinction”

Spencer-Brown introduces the elementary building block of his formal logic with the words ‘Draw a Distinction’. Figure 1 shows this very simple formal element:

​

Fig 1: The form of Spencer-Brown

A Radical Abstraction

In fact, his logic consists exclusively of this building block. Spencer-Brown has thus achieved an extreme abstraction that is more abstract than anything mathematicians and logicians have found so far.

What is the meaning of this form? Spencer-Brown is aiming at an elementary process, namely the ‘drawing of a distinction’. This elementary process now divides the world into two parts, namely the part that lies within the distinction and the part outside.

Fig. 2: Visualisation of the distinction

Figure 2 shows what the formal element of Fig. 1 represents: a division of the world into what is separated (inside) and everything else (outside). The angle of Fig. 1 thus becomes mentally a circle that encloses everything that is distinguished from the rest: ‘draw a distinction’.

The angular shape in Fig. 1 therefore refers to the circle in Fig. 2, which encompasses everything that is recognised by the distinction in question.

Perfect Continence

But why does Spencer-Brown draw his elementary building block as an open angle and not as a closed circle, even though he is referring to the closedness by explicitly saying: ‘Distinction is perfect continence’, i.e. he assigns a perfect inclusion to the distinction. The fact that he nevertheless shows the continence as an open angle will become clear later, and will reveal itself to be one of Spencer-Brown’s ingenious decisions.  ↝  imaginary logic value, to be discussed later.

Marked and Unmarked

In addition, it is possible to name the inside and the outside as the marked (m = marked) and the unmarked (u = unmarked) space and use these designations later in larger and more complex combinations of distinctions.

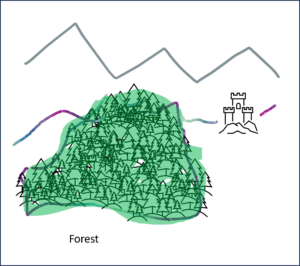
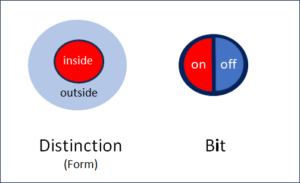
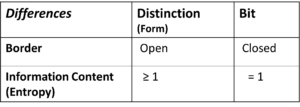
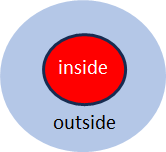
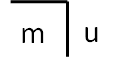​Fig. 3: Marked (m) and unmarked (u) space

Distinctions combined

To use the building block in larger logic statements, it can now be put together in various ways.

​

Fig. 4: Three combined forms of differentiation

Figure 4 shows how distinctions can be combined in two ways. Either as an enumeration (serial) or as a stacking, by placing further distinctions on top of prior distinctions. Spencer-Brown works with these combinations and, being a genuine mathematician, derives his conclusions and proofs from a few axioms and canons. In this way, he builds up his own formal mathematical and logical system of rules. Its derivations and proofs need not be of urgent interest to us here, but they show how carefully and with what mathematical meticulousness Spencer-Brown develops his formalism.

​Re-Entry

The re-entry is now what leads us to the paradox. It is indeed the case that Spencer-Brown’s formalism makes it possible to draw the formalism of real paradoxes, such as the barber’s paradox, in a very simple way. The re-entry acts like a shining gemstone (sorry for the poetic expression), which takes on a wholly special function in logical networks, namely the linking of two logical levels, a basic level and its meta level.

The trick here is that the same distinction is made on both levels. That it involves the same distinction, but on two levels, and that this one distinction refers to itself, from one level to the other, from the meta-level to the basic level. This is the form of paradox.

​Exemple Barber Paradox

We can now notate the Barber paradox using Spencer-Brown’s form:

 

Fig. 5: Distinction of the men in the village who shave themselves (S) or do not shave themselves (N)

​

Fig. 6: Notation of Fig. 5 as perfect continence

Fig. 5 and Fig. 6 show the same operation, namely the distinction between the men in the village who shave themselves and those who do not.

So how does the barber fit in? Let’s assume he has just got up and is still unshaven. Then he belongs to the inside of the distinction, i.e. to the group of unshaven men N. No problem for him, he shaves quickly, has breakfast and then goes to work. Now he belongs to the men S who shave themselves, so he no longer has to shave. The problem only arises the next morning. Now he’s one of those men who shave themselves – so he doesn’t have to shave. Unshaven as he is now, however, he is a men he has to shave. But as soon as he shaves himself, he belongs to the group of self-shavers, so he doesn’t have to be shaven. In this manner, the barber switches from one group (S) to the other (N) and back. A typical oscillation occurs in the barber’s paradox – and in all other real paradoxes, which all oscillate.

How does the Paradox Arise?
​

Fig. 7: The barber (B) shaves all men who do not shave themselves (N)

Fig. 7, shows the distinction between the men N (red) and S (blue). This is the base level. Now the barber (B) enters. On a logical meta-level, it is stated that he shaves the men N, symbolised by the arrow in Fig. 7.

The paradox arises between the basic and meta level. Namely, when the question is asked whether the barber, who is also a man of the village, belongs to the set N or the set S. In other words:

→  Is  B an  N  or an  S ?  

The answer to this question oscillates. If B is an N, then he shaves himself (Fig. 7). This makes him an S, so he does not shave himself. As a result of this second cognition, he becomes an N and has to shave himself. Shaving or not shaving? This is the paradox and its oscillation.

How is it created? By linking the two levels. The barber is an element of the meta-level (macro level), but at the same time an element of the base level (micro level). Barber B is an acting subject on the meta-level, but an object on the basic level. The two levels are linked by a single distinction, but B is once the subject and sees the distinction from the outside, but at the same time he is also on the base level and there he is an object of this distinction and thus labelled as N or S. Which is true? This is the oscillation, caused by the re-entry.

The re-entry is the logical core of all true paradoxes. Spencer-Brown’s achievement lies in the fact that he presents this logical form in a radically simple way and abstracts it formally to its minimal essence.

The paradox is reduced to a single distinction that is read on two levels, firstly fundamentally (B is N or S) and then as a re-entry when considering whether B shaves himself.

The paradox is created by the re-entry in addition to a negation: he shaves the men who do not shave themselves. Re-entry and negation are mandatory in order to generate a true paradox. They can be found in all genuine paradoxes, in the barber paradox, the liar paradox, the Russell paradox, etc.

Georg Spencer-Brown’s achievement is that he has reduced the paradox to its essential formal core:

→ A (single) distinction with a re-entry and a negation.

His discoveries of distinction and re-entry have far-reaching consequences with regard to logic, and far beyond.

Let’s continue the investigation, see:  Form (Distinction) and Bit

Translateion: Juan Utzinger

 

Information, Logic

Paradoxes and Logic (Part 1)

Leave a comment

Logic in Practice and Theory

Computer programs consist of algorithms. Algorithms are instructions on how and in what order an input is to be processed. Algorithms are nothing more than applied logic and a programmer is a practising logician.

But logic is a broad field. In a very narrow sense, logic is a part of mathematics; in a broad sense, logic is everything that has to do with thinking. These two poles show a clear contrast: The logic of mathematics is closed and well-defined, whereas the logic of thought tends to elude precise observation: How do I come to a certain thought? How do I construct my thoughts when I think? And what do I think just in this moment, when I think about my thinking? While mathematical logic works with clear concepts and rules, which are explicit and objectively describable, the logic of thinking is more difficult to grasp. Are there any rules for correct thinking, just as there are rules in mathematical logic for drawing conclusions in the right way?

When I look at the differences between mathematical logic and the logic of thought, something definitely strikes me: Thinking about my thinking defies objectivity. This is not the case in mathematics. Mathematicians try to safeguard every tiny step of thought in a way that is clear and objective and comprehensible to everyone as soon as they understand the mathematical language, regardless of who they are: the subject of the mathematician remains outside.

This is completely different with thinking. When I try to describe a thought that I have in my head, it is my personal thought, a subjective event that primarily only shows itself in my own mind and can only be expressed to a limited extent by words or mathematical formulae.

But it is precisely this resistance that I find appealing. After all, I wish to think ‘correctly’, and it is tempting to figure out how correct thinking works in the first place.

I could now take regress to mathematical logic. But the brain doesn’t work that way. In what way then? I have been working on this for many decades, in practice, concretely in the attempt to teach the computer NLP (Natural Language Processing). The aim has been to find explicit, machine-comprehensible rules for understanding texts, an understanding that is a subjective process, and – being subjective – cannot be easily brought to outside objectivity.

My computer programmes were successful, but the really interesting thing is the insights I was able to gain about thinking, or more precisely, about the logic with which we think.

My work has given me insights into the semantic space in which we think, the concepts that reside in this space and the way in which concepts move. But the most important finding concerned time in logic. I would like to go into that closer and for this target we first look at paradoxes.

Real Paradoxes

Anyone who seriously engages with logic, whether professionally or out of personal interest, will sooner or later come across paradoxes. A classic paradox, for example, is the barber’s paradox:

The Barber Paradox

The barber of a village is defined by the fact that he shaves all the men who do not shave themselves. Does the barber shave himself? If he does, he is one of the men who shave themselves and whom he therefore does not shave. But if he does not shave himself, he is one of the men he shaves, so he also shaves himself. As a result, he is one of the men he does not have to shave. So he doesn’t shave – and so on. That’s the paradox: if he shaves, he doesn’t shave. If he doesn’t shave, he shaves.

The same pattern can be found in other paradoxes, such as the liar paradox and many others. You might think that these kinds of paradoxes are far-fetched and don’t really play a role. But paradoxes do play a role, at least in two places: in maths and in the thought process.

Russell’s Paradox and Kurt Gödel’s Incompleteness Theorems

Russel’s paradox has revealed the gap in set theory. Its ‘set of all sets that does not contain itself as an element’ follows the same pattern as the barber of the barber paradox and leads to the same kind of unsolvable paradox. Kurt Gödel’s two incompleteness theorems are somewhat more complex, but are ultimately based on the same pattern. Both Russel’s and Gödel’s paradoxes have far-reaching consequences in mathematics. Russel’s paradox has led to the fact that set theory can no longer be formed using sets alone, because this leads to untenable contradictions. Zermelo had therefore supplemented the sets with classes and thus gave up the perfectly closed nature of set theory.

Gödel’s incompleteness theorems, too, are ultimately based on the same pattern as the Barber paradox. Gödel had shown that every formal system (formal in the sense of the mathematicians) must contain statements that can neither be formally proven nor disproven. A hard strike for mathematics and its formal logic.

Spencer-Brown and the “Laws of Form”

Russel’s refutation of the simple set concept and Gödel’s proof of the incompleteness of formal logic suggest that we should think more closely about paradoxes. What exactly is the logical pattern behind Russel’s and Gödel’s problems? What makes set theory and formal logic incomplete?

The question kept me occupied for a long time. Surprisingly, it turned out that paradoxes are not just annoying evils, but that it is worth using them as meaningful elements in a new formal logic. This step was exemplarily demonstrated by the mathematician Georg Spencer-Brown in his 1969 book ‘Laws of Form’, including a maximally simple formalism for logic.

I would now like to take a closer look at the structure of paradoxes, as Spencer-Brown has pointed them out, and the consequences this has for logic, physics, biology and more.

continue: Paradoxes and Logic (part2)

Translation: Juan Utzinger

 

Information, Logic

Five Preconceptions about Entropy

Leave a comment

Which of these Preconceptions do you Share?

  1. Entropy is for nerds
  2. Entropy is incomprehensible
  3. Entropy is thermodynamics
  4. Entropy is noise
  5. Entropy is absolute

Details

1. Entropy is the Basis of our Daily Lives

Nerds like to be interested in complex topics and entropy fits in well, doesn’t it? It helps them to portray themselves as superior intellectuals. This is not your game and you might not see any practical reasons to occupy yourself with entropy. This attitude is very common and quite wrong. Entropy is not a nerdy topic, but has a fundamental impact on our lives, from elementary physics to practical everyday life.

Examples (according to W. Salm1)

  • A hot coffee cup cools down over time
  • Water evaporates in an open container
  • Pendulums that have been knocked remain stationary after a while
  • Iron rusts
  • Magnets become weaker after some years
  • Lessons learnt are forgotten
  • Combed hair becomes dishevelled
  • White shirts become stained
  • Rocks crumble
  • Radioactive elements decay

So there are plenty of reasons to look into the phenomenon of entropy, which can be found everywhere in everyday life. But most people tend to avoid the term. Why is that? This is mainly due to the second preconception.

2. Entropy is a Perfectly Understandable and Indispensable Fundamental Concept

It is true, that at first glance, entropy is rather confusing. However, entropy is only difficult to understand because of persistent preconceptions (see points 4 and 5, below). These ubiquitous preconceptions are the obstacles that make the concept of entropy seem incomprehensible. Overcoming these thresholds not only helps to understand many real and practical phenomena, but also sheds light on the foundations that hold our world together.

3. Entropy Plays a Role Everywhere in Nature

The term entropy stems from thermodynamics. But we should not be mislead by this. In reality, entropy is something that exists everywhere in physics, chemistry, biology and also in art and music. It is a general and abstract concept and it refers directly to the structure of things and the information they contain.

Historically, the term was introduced not 200 years ago in thermodynamics and was associated with the possibility of allowing heat (energy) to flow. It helped to understand the mode of operation of machines (combustion engines, refrigerators, heat pumps, etc.). The term is still taught in schools this way.

However, thermodynamics only shows a part of what entropy is. Its general nature was only described by C.E. Shannon2 in 1948. The general form of entropy, also known as Shannon or information entropy, is the proper, i.e. the fundamental form. Heat entropy is a special case.

Through its application to heat flows in thermodynamics, entropy as heat entropy was given a concrete physical dimension, namely J/K, i.e. energy per temperature. However, this is the special case of thermodynamics, which deals with energies (heat) and temperature. If entropy is understood in a very general and abstract way, it is dimensionless, a pure number.

As the discoverer of abstract and general information entropy, Shannon gave this number a name, the “bit”. For his work as an engineer at the Bell telephone company, Shannon used the dimensionless bit to calculate the flow of information in the telephone wires. His information entropy is dimensionless and applies not only in thermodynamics, but everywhere where information and flows play a role.

4. Entropy is the Difference between not Knowing and Knowing

Many of us learnt at school that entropy is a measure of noise and chaos. Additionally, the second law of physics tells us that entropy can only ever increase. Thus, disorder should but increase. However, identifying entropy with noise or even chaos is misleading.

There are good reasons for this misleading idea: If you throw a sugar cube into the coffee, its well-defined crystal structure dissolves, the molecules disperse disorderly in the liquid and the sugar shows a transition from ordered to disordered. This decay of order can be observed everywhere in nature. In physics, it is entropy that drives the decay of order according to the second law. And decay and chaos can hardly be equated with Shannon’s concept of information. Many scientists thought the same way and therefore equated information with negentropy (entropy with a negative sign). At first glance, this doesn’t seem to be a bad match. In this view, entropy is noise and the absence of noise, i.e. negentropy, would then be information. Actually logical, isn’t it?

Not quite, because information is contained both in the sugar cube as well as in the dissolved sugar molecules floating in the coffee. In some ways, there is even more information in the individually floating molecules because each has its own path. Their bustling movements contain information. For us coffee drinker, however, the bustling movements of the many molecules in the cup does not contain useful information and appears only chaotic. Can this chaos be information?

The problem is our conventional idea of information. Our idea is too static. I suggest that we see entropy as something that denotes a flow, namely the flow between not knowing and knowing. This dynamic is characteristic of learning, of absorbing new information.

Every second, an incredible amount of things happen in the cosmos that could be known. The information in the entire world can only increase. This is what the second law says, and what increases is entropy, not negentropy. Wouldn’t it be much more obvious to put information in parallel with entropy and not with negentropy? More entropy would then mean more information and not more chaos.

Where can the information be found? In the noise or in the absence of noise? In entropy or in negentropy?

Two Levels

Well, the dilemma can be solved. The crucial step is to accept that entropy is the tension between two states, the overview state and the detail state. The overview view does not need the details, but only sees the broad lines. C.F. Weizsäcker speaks of the macro level. The broad lines are the information that interests us. Details, on the other hand, appear to us as unimportant noise. But the details, i.e. the micro level, contain more information, usually a whole lot more, just take the movements of the water molecules in the coffee cup (micro level), whose chaotic bustle contains more information than the single indication of the temperature of the coffee (macro level). Both levels are connected and their information depends on each other in a complex way. Entropy is the difference between the two amounts of information. This is always greater at the detail level (micro level), because there is always more to know in the details than in the broad lines and therefore also more information.

But because the two levels refer to the same object, you as the observer can look at the details or the big picture. Both belong together. The gain in information about details describes the transition from the macro to the micro level, the gain in information about the overview describes the opposite direction.

So where does the real information lie? At the detailed level, where many details can be described, or at the overview level, where the information is summarised and simplified in a way that really interests us?

The answer is simple: information contains both the macro and the micro level. Entropy is the transition between the two levels and, depending on what interests us, we can make the transition in one direction or the other.

Example Coffee Cup

This is classically demonstrated in thermodynamics. The temperature of my coffee can be seen as a metric for the average kinetic energy of the individual liquid molecules in the coffee cup. The information contained in the many molecules is the micro state, the temperature is the macro state. Entropy is the knowledge that is missing in the macro state but is present in the micro state. But for me as a coffee drinker, only the knowledge of the macro state, the temperature of the coffee, is relevant. This is not present in the micro state insofar as it does not depend on the individual molecules, but rather statistically on the totality of all molecules. It is only in the macro state that knowledge about temperature becomes tangible.

For us, only the macro state shows relevant information. But there is additional information in the noise of the details. How exactly the molecules move is a lot of information, but these details don’t matter to me when I drink coffee, only their average speed determines the temperature of the coffee, which is what matters to me.

The information-rich and constantly changing microstate has a complex relationship with the simple macroinformation of temperature. The macro state also influences the micro state, because the molecules have to move within the statistical framework set by the temperature. Both pieces of information depend on each other and are objectively present in the object at the same time. What differs is the level or scope of observation. The difference in the amount of information in the two levels determines the entropy.​

These conditions have been well known since Shannon2 and C.F. Weizsäcker. However, most schools still teach that entropy is a measure of noise. This is misleading. Entropy should always be understood as a delta, as a difference (distance) between the information in the overview (macro state) and the information in the details (micro state).

5. Entropy is a Relative Value

The fact that entropy is always a distance, a delta, i.e. mathematically a difference, also results in the fact that entropy is not an absolute value, but rather a relative value.

Example Coffee Cup
Let’s take the coffee cup as an example. How much entropy is in there? If we only look at the temperature, then the microstate corresponds to the average kinetic energy of the molecules. But the coffee cup contains even more information: How strong is the coffee? How strongly sweetened? How strong is the acidity? What flavours does it contain?

Example School Building
Salm1 gives the example of a lost door key that a teacher is looking for in a school building. If he knows which classroom the key is in, he has not yet found it. At this moment, the microstate only names the room. Where in the room is the key? Perhaps in a cupboard. In which one? At what height? In which drawer, in which box? The micro state varies depending on the depth of the request. It is a relative value. 

Because the information entropy is always a difference, the entropy, i.e. the span between overview and details, can always be extended to even more details.

Entropy is a relative value. If we specify it in absolute terms, we set – without explicitly declaring it – a lowest level (classroom, shelf or drawer). This is legal as long as we are aware that the seemingly absolute value only represents the distance to the assumed micro-level.

Statics and Dynamics 

Energy and entropy are two complementary quantities that permeate the entire description of nature (physics, chemistry, biology). The two fundamental laws of physics each contain one of the two general quantities E (energy) and S (entropy):

  1. Law:  ∆E = 0    oder:   dE/dt = 0
  2. Law:  ∆S ≥ 0    oder:   dS/dt ≥ 0

Energy remains constant over time (in a closed system), while entropy can only increase. In other words: energy is a static value and shows what does not change, while entropy is essentially dynamic and shows flows, e.g. in heat machines, in Shannon’s current in telephone wires and whenever our thoughts flow and we learn and think.

Entropy and Time

Entropy is essentially linked to the phenomenon of time by the second law (∆S ≥ 0). While energy remains constant in a closed system (Noether’s theorem), entropy changes over time and increases in a closed system. Entropy therefore knows time, not only heat entropy in particular, but also the much more general information entropy.

Conclusion

  • Entropy is a key concept in physics and information theory.
  • The term entropy comes from thermodynamics, but the concept of entropy refers to information in general.
  • ​The thermodynamical entropy is the special case, information entropy is the general concept.
  • Everything that happens physically, chemically and in information processing, whether technical or biological, has to do with entropy. In particular, everything that has to do with information flows and structures. In other words, everything that really interests us.
  • Entropy is always relative and refers to the distance between the macro and micro levels.
  • The macro level contains less information than the micro level
  • The macro level contains the information of interest.
  • Neither is absolute: the micro level can always be described in more detail. The macro level is defined from the outside: What is of interest? The temperature of the coffee? The concentration of sugar molecules? The acidity? The caffeine content …
  • Only the definition of the two states makes it possible to specify the entropy in seemingly absolute terms. However, what counts for entropy is the relative value, i.e. the delta between the two states. This delta, the entropy, determines the flow.
  • The flow happens in time.

(Translation: Juan Utzinger)

1 Salm, W: Entropie und Information – naturwissenschaftliche Schlüsselbegriffe, Aulis Verlag Deubner, Köln, 1997

2 Shannon, C.E. und Weaver W: The Mathematical Theory of Information, Illinois Press, Chicago, 1949

See also: What is Entropy?

Information

Combinatorial explosion

Leave a comment

Objects and relations

Let us first take a set of objects and consider how many connections (relations) there are between them, leaving aside the nature of the relationships and focussing solely upon their number. This is quite a simple task, because there is always exactly one relation between any two objects. Even if the two objects are entirely unrelated, this fact has a meaning and is thus useful information. We can count the number of possible connections between the objects and compare the number of objects with the number of possible relations.

7 Objekte und ihre Relationen

Fig 1: Seven objects and their relations

Figure 1 shows seven objects (blue) and their relations (red). Every object is connected to every other object. Thus, in our example, each of the 7 objects is connected to 7-1 = 6 other objects, giving a total of 7 * 6 / 2 = 21 relations. The general mathematical formula for this is NR = (NO2 – NO) / 2, where NR is the number of relations and NO is the number of objects.
As we can see from the formula, the number of relations increases in proportion to the square of the number of objects. Or, to put it non-mathematically:

There are always a great many more relations than there are objects!

Below is a small table showing the number of relations for a given number of objects:

NO  NR
———————-
1    0
2    1
3    3
4    6
5    10
6    15
7    21
8    28
9    36
10     45
100   4,950
1000    499,500

Table 1: Objects and relations

While the numbers in the first column are small, the quadratic increase is not particularly noticeable. However, as these numbers rise it quickly becomes more marked. Before we turn our attention to the practical implications of this, let us first take a look at the number of possible combinations.

Objects and combinations

The term ‘combination’ refers to the ways in which a number of objects can be combined with each other. Whereas a relation always relates to precisely two objects, combinations can include any number of objects from 1 to all (= NO).

Tab 2: Objekte und Kombinationen

Table 2: Objects and combinations

Table 2 shows objects and the number of combinations between them for 1 to 4 objects, with the number of objects in the first column and the number of combinations in the second. The objects are identified by letters (a, b, c ,d) and the possible combinations are shown in the column on the far right. When there is only one object (a) there is just one combination consisting solely of this element; when there are 2 the number of combinations rises to 3 and when there are 4 it is 15. The number of combinations per object therefore increases even faster than the number of relations (as described above). The formula for this is: NC = 2No – 1.

As we saw earlier, the relationship between objects and their relations is quadratic. The relationship between objects and combinations, on the other hand, is based upon exponential growth, meaning that it rises even more quickly. When there are 10 objects, the number of combinations is 1023; when there are 100, this figure rises to an incredible 1,267,650,600,600,228,229,429,401,496,703,205,375 or 1.26 * 1036 !

 The number of combinations thus increases extremely rapidly.

This exponential increase forms the basis for the combinatorial explosion.

Combinatorial explosion

Let’s suppose we have a number of different objects with different properties, for example:

4 shapes: round, square, triangular, star-shaped.
8 colours: red, orange, yellow, green, blue, brown, white, black.
7 materials: wood, PVC, aluminium, cardboard, paper, glass, stone.
3 sizes: small, medium-sized, large.

We can now combine these four classes and their 22 properties in any way we want. For example, an object may be triangular, green, medium-sized and made of PVC. Based upon these 22 properties, how many different types of objects can we distinguish between?

We can select one property independently from each of the four classes (shape, colour, material, size), giving a total of 4x8x7x3 = 672 possible combinations. This means that, if there are 22 properties, we can describe 672 different objects. For every additional class, the number of possibilities is multiplied.

It doesn’t take many additional classes before the number of possible combinations explodes.

This is the combinatorial explosion. And it plays a critical role in any information processing – especially when the information relates to the real world, where the number of classes has no natural limit.

Information

Information Reduction 7: Micro and Macro State

Leave a comment

Examples of information reduction

In previous texts we looked at examples of information reduction in the following areas:

  • Coding / classification
  • Sensory perception
  • DRG (Flat rate per case)
  • Opinion formation
  • Thermodynamics

What do they have in common?

Micro and macro state

What all these examples have in common is that, in terms of information, there are two states: a micro state with a great many details and a macro state with much less information. One very clear example that many of us will remember from our school days is the relationship between the two levels in thermodynamics.

The two states exist simultaneously, and have less to do with the object itself than with the perspective of the observer. Does he need to know everything, down to the last detail? Or is he more interested in the essence, i.e. the simplified information of the macro state?

Micro and macro state in information theory

The interplay of micro and macro states was first recognised in thermodynamics. In my opinion, however, this is a general phenomenon, which is closely linked to the process of information reduction. It is particularly helpful to differentiate between the two states when investigating information processing in complex situations.
Wherever the amount of information is reduced, a distinction can be drawn between a micro and a macro state. The micro state is the one that contains more information, the macro state less. Both describe the same object, but from different perspectives.

The more detailed micro state is considered to be ‘more real’

We tend to think we are seeing something more clearly if we can discern more details. So we regard the detailed micro state as the actual reality and the macro state as either an interpretation or a consequence of this.

… but the low-information macro state is more interesting

Remarkably, however, the low-information state is of more interest to us than the micro state. In the micro state, there are simply too many details. These are either irrelevant to us (thermodynamics, sensory perception) or they obstruct our clear view of the goal represented by the macro state (coding, classification, opinion-forming, flat rate per case).

Strange antagonism

There is thus a strange antagonism between the two states, with one seeming more real and the other more relevant, as if these two qualities were somehow at odds with one another. The more detailed the information, the less the many single data points have to do with the overall perspective, which thus increasingly disappears from sight. On the other hand: the more intensively the view strives for relevance, the more it detaches itself from the details of reality. This paradoxical relationship between micro and macro state is characteristic of all information reduction relationships and highlights both the importance of, and the challenges associated with, such processes.

Are there differences between the various processes of information reduction?

Absolutely. The only thing they have in common is that it is possible to display the data at a detailed micro level or at a macro level containing little information, with the latter usually being more relevant.

Such processes always involve a reduction in information, but the way in which it is reduced differs. At this point it would be illuminating to examine the differences – which play a decisive role in many issues – more closely. Read more in next post.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 6: The Waterglass, Revisited

Leave a comment

Is that physics?

In my article Information reduction 5: The classic glass of water, I drew upon the example of a glass of water to illustrate the principle of information reduction. In this example, the complex and detailed information about the kinetic energy of water molecules (micro level) is reduced to simple information about the temperature of the water.

Of course, a physicist might criticise this example – and quite rightly so, because the glass of water is actually much more complicated than this. Boltzmann’s calculations only apply to the ideal gas, i.e. one whose molecules do not interact except when they collide and exchange their individual movement information.

An ideal gas

The ideal gas is an idealisation you won’t find anywhere in the real world. Other forces exist between individual molecules than the purely mechanical ones, and the situation in our glass of water is no different. Because water is a liquid not a gas and because much stronger bonds exist between molecules in liquids than between gas molecules, these additional bonds complicate the picture.

Water

Moreover, water is a special case. The water molecule (H2O) is a strong dipole, which means it has a strong electrical charge difference between its two poles, the negatively charged pole with the oxygen atom (O) and the positively charged pole with the two hydrogen atoms (H2). As a result of this strong polarity, multiple water molecules join together. If such agglomerations were to be maintained, the water would be a solid (such as ice) rather than a liquid. But since they are only temporary, the water remains a liquid, but a special one that behaves in a very particular way. See, for example, the current research of Gerald Pollack.

Physics and information science

A glass of water probably isn’t the example a physicist would have chosen, but I’m not going to change it. It’s as good an example as any to explain the ratio of information at the micro and macro levels. Boltzmann’s calculations are only approximately correct, but his thesis holds: the temperature of an object is the macro-level information that summarises the many data points about the chaotic movements of the individual molecules at the micro level.

The glass of water may be a bad example to a physicist.  For our consideration about micro and macro states, however, it makes no difference whether we are considering an ideal gas or a glass of water: there is always a huge information gap between the macro state and the micro state, and that is the salient point. In a glass of water, the micro state contains billions of times more information than the macro state. And, interestingly, although the micro state is richer in information, it is the macro state that is of greater interest to us.

The transition

How does the transition from micro to macro state take place in different cases? Clearly, this transition is slightly different in the glass of water than in the ideal gas due to the special properties of the H2O molecule. And the transition from the micro to the macro state is completely different in our other examples of classification, concept formation and framing that are not drawn from the physical world. We will now go into these peculiarities. See the posts to come.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information, Logic

Is ‘IF-THEN’ static or dynamic?

Leave a comment
IF-THEN and Time

It’s a commonly held belief that there’s nothing complicated about the idea of IF-THEN from the field of logic. However, I believe this overlooks the fact that there are actually two variants of IF-THEN that differ depending on whether the IF-THEN in question possesses an internal time element.

Dynamic (real) IF-THEN

For many of us, it’s self-evident that the IF-THEN is dynamic and has a significant time element. Before we can get to our conclusion – the THEN – we closely examine the IF – the condition that permits the conclusion. In other words, the condition is considered FIRST, and only THEN is the conclusion reached.

This is the case not only in human thinking, but also in computer programs. Computers allow lengthy and complex conditions (IFs) to be checked. These must be read from the computer’s memory by its processor. It may be necessary to perform even smaller calculations contained in the IF statements and then compare the results of the calculations with the set IF conditions. These queries naturally take time. Even though the computer may be very fast and the time needed to check the IF minimal, it is still measurable. Only AFTER checking can the conclusion formulated in the computer language – the THEN – be executed.

In human thinking, as in the execution of a computer program, the IF and the THEN are clearly separated in time. This should come as no surprise, because both the sequence of the computer program and human thinking are real processes that take place in the real, physical world, and all real-world processes take time.

Static (ideal) IF-THEN

It may, however, surprise you to learn that in classic mathematical logic the IF-THEN takes no time at all. The IF and the THEN exist simultaneously. If the IF is true, the THEN is automatically and immediately also true. Actually, even speaking of a before and an after is incorrect, since statements in classical mathematical logic always take place outside of time. If a statement is true, it is always true, and if it is false, it is always false (= monotony, see previous posts).

The mathematical IF-THEN is often explained using Venn diagrams (set diagrams). In these visualisations, the IF may, for example, be represented by a set that is a subset of the THEN set. For mathematicians, IF-THEN is a relation that can be derived entirely from set theory. It’s a question of the (unchangeable) states of true or false rather than of processes, such as thinking in a human brain or the execution of a computer program.

Thus, we can distinguish between
  • Static IF-THEN:
    In ideal situations, i.e. in mathematics and in classical mathematical logic.
  • Dynamic IF-THEN:
    In real situations, i.e. in real computer programs and in the human brain.
Dynamic logic uses the dynamic IF-THEN          

If we are looking for a logic that corresponds to human thinking, we must not limit ourselves to the ideal, i.e. static, IF-THEN. The dynamic IF-THEN is a better match for the normal thought process. This dynamic logic that I am arguing for takes account of time and needs the natural – i.e. the real and dynamic – IF-THEN.

If time is a factor and the world may be a slightly different place after the first conclusion has been drawn, it matters which conclusion is drawn first. Unless you allow two processes to run simultaneously, you cannot draw both conclusions at the same time. And even if you do, the two parallel processes can influence each other, complicating the matter still further. For this reason along with many others, dynamic logic is much more complex than the static variant. This increases our need for a clear formalism to help us deal with this complexity.

Static and dynamic IF-THEN side by side

The two types of IF-THEN are not mutually exclusive; they complement each other and can coexist. The classic, static IF-THEN describes logical states that are self-contained, whereas the dynamic variant describes logical processes that lead from one logical state to another.

This interaction between statics and dynamics is comparable with the situation in physics, where we find statics and dynamics in mechanics, and electrostatics and electrodynamics in the study of electricity. In these fields, too, the static part describes the states (without time) and the dynamic part the change of states (with time).

This is a blog post about dynamic logic. The next post specifies the topic of the dynamic IF-THEN.

Information

Information Reduction 5: The Classic Glass of Water

Leave a comment
Information reduction in thermodynamics

A very specific example of information reduction can be found in the field of thermodynamics. What makes this example so special is its simplicity. It clearly illustrates the basic structure of information reduction without the complexity found in other examples, such as those from biology. And it’s a subject many of us will already be familiar with from our physics lessons at school.

What is temperature?

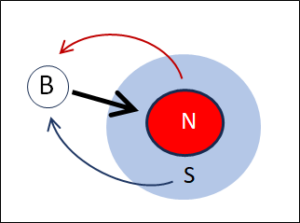
A glass of water contains a huge amount of water molecules, all moving at different speeds and in different directions. These continuously collide with other water molecules, and their speed and direction of travel changes with each impact. In other words, the glass of water is a typical example of a real object that contains more information than an external observer can possibly deal with.

That’s the situation for the water molecules. So what is the temperature of the water in the glass?

As Ludwig Boltzmann was able to demonstrate, temperature is simply the result of the movement of the many individual water molecules in the glass. The faster they move, the more energy they have and the higher is the temperature of the water As Ludwig Boltzmann explained, the temperature of the water in the glass can be calculated statistically from the kinetic energy of the many molecules. Billions of molecules with their constantly changing motion produce exactly one temperature. Thus, a large amount of information is converted into a single fact.

The micro level and the macro level

It’s worth noting that the concept of temperature cannot be applied to individual molecules. At this level, there is only the movement of many single molecules, which changes with each impact. The kinetic energy of the molecules depends on their speed and thus changes with each impact.

Although the motion of the water molecules is constantly changing at the micro level, the temperature at the macro level of the glass of water remains comparatively constant. And, in the event that it does change, for example because heat is given off from the water at the walls of the glass, there are formulas that can be used to calculate the movement of the heat and thus the change in temperature. These formulas remain at the macro level, i.e. they do not involve the many complicated impacts and movements of the water molecules.

The temperature profile can thus be described and calculated entirely at the macro level without needing to know the details of the micro level and its vast number of water molecules. Although the temperature (macro level) is defined entirely and exclusively by the movement of the molecules (micro level), we don’t need to know the details to predict its value. The details of the micro level seem to disappear at the macro level. This is a typical case of information reduction.

In the next post I’ll make some precisions concerning the waterglass.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 4: Framing

Leave a comment
Framing matters

The framing effect is a topic that comes up a lot these days. Framing is the phenomenon whereby the same message is perceived differently, depending on what additional information is sent with it. The additional information is provided to give the message the right ‘frame’ so that recipients respond appropriately.

Even if the additional information is undoubtedly true, the recipient can be genuinely manipulated by framing, simply by the selection of details that are in themselves factually correct. Framing is, of course, used in advertising, but its role in political reporting has become something of a hot topic of late.

Of course, framing in politics and advertising always involves choosing words that connect an item of information to the corresponding emotional content. But the simple fact that some aspects (details) of events are drawn into the foreground and some pushed into the background changes the image that the recipient forms of the message. For example, our response to the fact that a lot of refugees/migrants want to come to Europe depends on which of the many people we have in mind and which of the diverse range of aspects, reasons, circumstances and consequences of their journey we focus on. Reports about the criminal activities of individual migrants evoke a completely different image from descriptions of the inhuman, unfathomably awful conditions of the journey. That people are coming is a fact. But the way this fact is evaluated – its interpretation – is a matter of simplification, i.e. the selection of data. This brings us clearly to the phenomenon of information reduction.

Framing and information reduction

Real-world situations always contain much more detail than we can process. And because this means we always need to simplify them, information selection plays a crucial role: what do we bring to the forefront and what do we push into the background? The answer to this question colours our perception and thus our opinion. This phenomenon of information reduction is the same as that encountered in medical coding, where a variety of characteristics are drawn upon – or disregarded – in the assignment of codes (see article Two types of coding 1). The reduction and selection of information is part of all perception processes, and our actions and decisions are always based upon simplifications. The selection of details is what shapes our perception, and this selection depends not upon the object being viewed, but on the subject making the selection.

Diverging interpretations are possible (see previous article)

Reality (top of the diagram) is made up of all the facts, but our interpretation of it is always based upon a selection from this vast array of detail. This may lead us to form a range of different opinions. I believe that this phenomenon of information reduction (the interpretation phenomenon) is both fundamental and inescapable, and that it plays an important role in a wide range of different contexts. The framing effect is a typical example, but it is one of many.

Links to framing (in German):
– Spiegel article “Ab jetzt wird zurückgeframt” of 22.2.2019
– Wikipedia.de on the framing effect
– Interview with communication trainer Benedikt Held

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 3: Information is Selection

Leave a comment
Information reduction is everywhere

In a previous post, I described how the coding of medical facts – a process that leads from a real-world situation to a flat rate per case (DRG) – involves a dramatic reduction in the amount of information:

Informationsreduktion

Information reduction

This information reduction is a very general phenomenon and by no means limited to information and its coding in the field of medicine. Whenever we notice something, our sensory organs – for example our retinas – reduce the amount of information we take in. Our brain then simplifies the data further so that only the essence of the impressions, the part that is important to us, arrives in our consciousness.

Information reduction is necessary

If you ask someone how much they want to know, most people will tell you that they want to know as much as possible. Fortunately, this wish is not granted. Many will have heard of the savant who, after flying over a city just once, was able to draw every single house correctly from memory. Sadly, the same individual was incapable of navigating his everyday life unaided – the flood of information got in the way. So knowing every last detail is definitely not something to aspire to.

Information reduction means selection

If it is necessary and desirable to lose data, the next question concerns which data we should lose and which we should retain. Some will imagine that this is a natural choice, with the object we are looking at determining which data is important and which is not. In my opinion, this assumption is simply wrong. It is the observer who decides which information is important to him and which he can disregard. The information he chooses to retain will depend upon his goals.

Of course, the observer cannot get information out of the object that the object does not contain. But the decision as to which information he considers important is down to him – or to the system he feels an allegiance to.

This is particularly true in the field of medicine. What is important is the information about the patient that allows the doctor to make a meaningful diagnosis – and the system of diagnoses depends essentially on what can be treated and how. Medical progress means that the aspects and data that come into play will change over time.

In other words, we cannot know everything, and we must actively reduce the amount of information available so that we can make decisions and act. Information reduction is inevitable and always involves making a choice.

Different selections are possible

Which information is lost and which is retained? The answer to this question determines what we see when we look at an object.

Interpretation der Realität

Various information selections (interpretations) are possible

Because the observer – or the system that he lives in and that moulds and shapes his thinking – decides which information to keep, different selections are possible. Depending on which features we prioritise, different individual cases may be placed in a given group or category and different viewers will thus arrive at different interpretations of the same reality.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 2: The Funnel

Leave a comment
The funnel of information reduction

In my previous article Information reduction 1, I described a chain of information processing from the patient to the flat rate per case (DRG):

This acts as a funnel, reducing the amount of information available at each step.  The extent of the reduction is dramatic. Imagine we have the patient in front of us. One aspect of a comprehensive description of this patient is their red blood cells. There are 24-30 trillion (= 24–30·1012 ) red blood cells in the human body, each with a particular shape and location in the body, and each moving in a particular way at any given time and containing a certain amount of red blood pigment. That is indeed a lot of information. But, of course, we don’t need to know all these details. As a rule, it is sufficient to know whether there is enough red blood pigment (haemoglobin) in the bloodstream. Only if this is not the case (as with anaemia) do we want to know more. Thus, we reduce the information about the patient, selecting only that which is necessary. This is entirely reasonable, even though we lose information in the process.

The funnel, quantified

To quantify how much information reduction takes place, I have cited the number of possible states at each stage of information processing in the above figure. From bottom to top, these are as follows:

  • DRGs (flat rates per case): There are various DRG systems. However, there are always about 1000 different flat rates, i.e. 103 At the level of the flat rate per case, therefore, 103 different states are possible. This is the information that is available at this level.
  • Codes: In Switzerland, the ICD-10 classification system offers 15,000 different codes Let us assume, as an approximation, that each patient has two diagnoses. So we can choose between 15,000 states twice, giving 225,000,000 = 2.25 x
  • 108
  • .
  • Texts: SNOMED, an extensive medical nomenclature, contains about 500,000 (5 x 105) different expressions. Since a medical record contains a great many words, the amount of information here is naturally much more detailed. My estimate of 1015 is definitely on the low side.
  • Perception and reality: I won’t make an estimate. The above example involving red blood cells illustrates the huge amounts of information available in real-world situations.

Read more in Information reduction 3

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford