Starting position
Do the criteria which we have postulated so far already enable us to create musical scales which are so attractive that they occur in reality? After all, the criteria look rather artificial and theoretical at first sight – can they nonetheless serve to explain musical scales that have grown naturally?
Indeed they can. The mathematical criteria for resonance have obviously had an impact on the human ear and have for millennia prompted people again and again to invent music which is fundamentally structured by precisely those musical scales that we are able to derive mathematically with the help of our criteria.
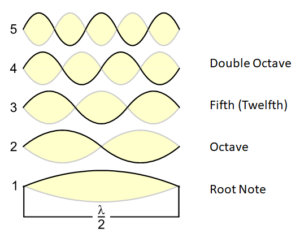
Pool of resonant tones
With our resonance criteria alone, we established a first pool which contains those tones of which we expect the strongest resonance with the fundamental tone. I list these nine potential scale tones again below:

Of course this is merely a pool of many tones, and not a meaningful musical scale. The problem is that all these tones can easily and quickly resonate with the fundamental tone – but do they also resonate among each other?
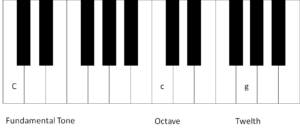
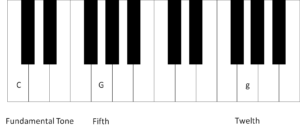
Two scale tones and the fundamental tone
Thus this is not solely about the resonance of a tone with the fundamental tone, but additionally about its resonance with other tones. This has a mathematical basis: we have a look at the lcm (least common multiple) of the denominators involved. How this works, and why this is the case, is explained on the page of calculation principles for resonances.
The lcm (least common multiple) of the denominators
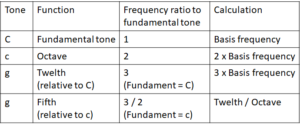
The resonance criteria indicate a good resonance if the lcm of the denominators involved is as small as possible. The fundamental tone has the denominator 1 and therefore fits every lcm; therefore it will fit every combination well. But how do the scale tones fit each other?
Example 1
Fourth and fifth: The denominators are 3 and 2; the lcm is 6, i.e. low. The numerators are also low. By way of a further indication of resonance, we can calculate the distance between the two tones. This is 3/2 : 4/3 = 9/8, i.e. a major second. Although 8 is a relatively high denominator, which may interfere with the resonance with other scale tones, both the 8 of the second and 2 of the fifth fit the very important octave very well. Also, both the fourth and the fifth have unbeatably low numerators and denominators, which has a favourable impact on the mixing ratios for further scale tones.
In other words: the fourth and the fifth are a perfect pair for resonance – at least mathematically. But does this also sound good?
How does the combination sound in our subjective perception?
Naturally, this is not solely about mathematics. The mental world, our subjective perception, determines whether we like a certain type of music and how we receive it. If you sound the fundamental tone along with the fourth, the fifth and the octave, you can hear what we have calculated: the resonance of the four tones is pure. Indeed, the combination even sounds rather banal, and we may miss the pep that dissonances introduce into the music to which we are accustomed. We also miss the sweetness of the thirds (denominators 5 and 6).
Example 2
We mathematically combine the major second with the minor third, i.e. 9/8 with 6/5: the lcm is 40, the interval between the two tones is 6/5 : 9/8 = 48/45 = 16/15. With the high lcm and the short distance, this pair is a bit more problematical – at least if we pay attention to good resonance and want to avoid any stridency in music.
The first two musical scales found
If you feel like it, you can calculate the lcm and the distance between all the above-mentioned yourself and thus compile a pool of tones in which both aspects are optimised and as much resonance as possible can develop. Of course you also want to select more than just three of four tones for a musical scale. What about five?
The two musical scales with the strongest resonance that can be found in this way are remarkable – both of them are very well-known musical scales:
1 – 9/8 – 5/4 – 3/2 – 5/3 – 2
1 – 6/5 – 4/3 – 3/2 – 9/5 – 2
Or with the fundamental tone C:
C – D – E – G – A – C
C – Es – F – G – Bb – C
Pentatonic scales
These are two pentatonic scales, i.e. two musical scales with five tones (the C occurs twice but is only counted once). It is not really surprising that both musical scales are good old friends – they are none other than the major and minor pentatonics.
Nor does it come as a surprise that both these musical scales occur in practically all the world’s cultures from the rain forest to all the advanced civilisations, either in their pure form or else as the basic structure of more sophisticated musical scales.
Theoretical and mathematical considerations have led us to postulate these two musical scales which are not only well-known worldwide but are easy to understand for everybody and felt to be catchy by everyone, including small children.
In my view, this is not an accident. It looks as if considerations so far are highly compatible with observed reality.
In the following post, you can find a resonance analysis of the five standard pentatonics.
This is a post about the theory of the three worlds.