Information, Logic

Is ‘IF-THEN’ static or dynamic?

Leave a comment
IF-THEN and Time

It’s a commonly held belief that there’s nothing complicated about the idea of IF-THEN from the field of logic. However, I believe this overlooks the fact that there are actually two variants of IF-THEN that differ depending on whether the IF-THEN in question possesses an internal time element.

Dynamic (real) IF-THEN

For many of us, it’s self-evident that the IF-THEN is dynamic and has a significant time element. Before we can get to our conclusion – the THEN – we closely examine the IF – the condition that permits the conclusion. In other words, the condition is considered FIRST, and only THEN is the conclusion reached.

This is the case not only in human thinking, but also in computer programs. Computers allow lengthy and complex conditions (IFs) to be checked. These must be read from the computer’s memory by its processor. It may be necessary to perform even smaller calculations contained in the IF statements and then compare the results of the calculations with the set IF conditions. These queries naturally take time. Even though the computer may be very fast and the time needed to check the IF minimal, it is still measurable. Only AFTER checking can the conclusion formulated in the computer language – the THEN – be executed.

In human thinking, as in the execution of a computer program, the IF and the THEN are clearly separated in time. This should come as no surprise, because both the sequence of the computer program and human thinking are real processes that take place in the real, physical world, and all real-world processes take time.

Static (ideal) IF-THEN

It may, however, surprise you to learn that in classic mathematical logic the IF-THEN takes no time at all. The IF and the THEN exist simultaneously. If the IF is true, the THEN is automatically and immediately also true. Actually, even speaking of a before and an after is incorrect, since statements in classical mathematical logic always take place outside of time. If a statement is true, it is always true, and if it is false, it is always false (= monotony, see previous posts).

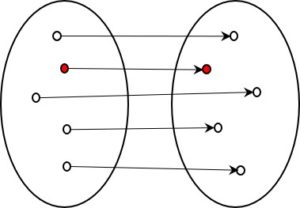
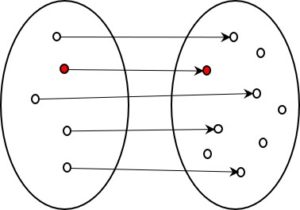
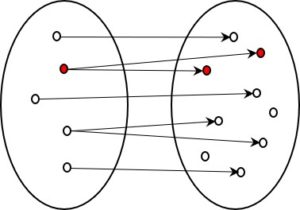
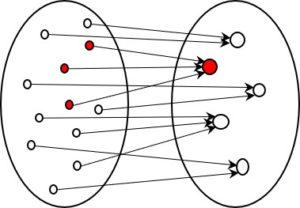
The mathematical IF-THEN is often explained using Venn diagrams (set diagrams). In these visualisations, the IF may, for example, be represented by a set that is a subset of the THEN set. For mathematicians, IF-THEN is a relation that can be derived entirely from set theory. It’s a question of the (unchangeable) states of true or false rather than of processes, such as thinking in a human brain or the execution of a computer program.

Thus, we can distinguish between
  • Static IF-THEN:
    In ideal situations, i.e. in mathematics and in classical mathematical logic.
  • Dynamic IF-THEN:
    In real situations, i.e. in real computer programs and in the human brain.
Dynamic logic uses the dynamic IF-THEN          

If we are looking for a logic that corresponds to human thinking, we must not limit ourselves to the ideal, i.e. static, IF-THEN. The dynamic IF-THEN is a better match for the normal thought process. This dynamic logic that I am arguing for takes account of time and needs the natural – i.e. the real and dynamic – IF-THEN.

If time is a factor and the world may be a slightly different place after the first conclusion has been drawn, it matters which conclusion is drawn first. Unless you allow two processes to run simultaneously, you cannot draw both conclusions at the same time. And even if you do, the two parallel processes can influence each other, complicating the matter still further. For this reason along with many others, dynamic logic is much more complex than the static variant. This increases our need for a clear formalism to help us deal with this complexity.

Static and dynamic IF-THEN side by side

The two types of IF-THEN are not mutually exclusive; they complement each other and can coexist. The classic, static IF-THEN describes logical states that are self-contained, whereas the dynamic variant describes logical processes that lead from one logical state to another.

This interaction between statics and dynamics is comparable with the situation in physics, where we find statics and dynamics in mechanics, and electrostatics and electrodynamics in the study of electricity. In these fields, too, the static part describes the states (without time) and the dynamic part the change of states (with time).

This is a blog post about dynamic logic. The next post specifies the topic of the dynamic IF-THENs.

Information

Information Reduction 5: The Classic Glass of Water

Leave a comment
Information reduction in thermodynamics

A very specific example of information reduction can be found in the field of thermodynamics. What makes this example so special is its simplicity. It clearly illustrates the basic structure of information reduction without the complexity found in other examples, such as those from biology. And it’s a subject many of us will already be familiar with from our physics lessons at school.

What is temperature?

A glass of water contains a huge amount of water molecules, all moving at different speeds and in different directions. These continuously collide with other water molecules, and their speed and direction of travel changes with each impact. In other words, the glass of water is a typical example of a real object that contains more information than an external observer can possibly deal with.

That’s the situation for the water molecules. So what is the temperature of the water in the glass?

As Ludwig Boltzmann was able to demonstrate, temperature is simply the result of the movement of the many individual water molecules in the glass. The faster they move, the more energy they have and the higher is the temperature of the water As Ludwig Boltzmann explained, the temperature of the water in the glass can be calculated statistically from the kinetic energy of the many molecules. Billions of molecules with their constantly changing motion produce exactly one temperature. Thus, a large amount of information is converted into a single fact.

The micro level and the macro level

It’s worth noting that the concept of temperature cannot be applied to individual molecules. At this level, there is only the movement of many single molecules, which changes with each impact. The kinetic energy of the molecules depends on their speed and thus changes with each impact.

Although the motion of the water molecules is constantly changing at the micro level, the temperature at the macro level of the glass of water remains comparatively constant. And, in the event that it does change, for example because heat is given off from the water at the walls of the glass, there are formulas that can be used to calculate the movement of the heat and thus the change in temperature. These formulas remain at the macro level, i.e. they do not involve the many complicated impacts and movements of the water molecules.

The temperature profile can thus be described and calculated entirely at the macro level without needing to know the details of the micro level and its vast number of water molecules. Although the temperature (macro level) is defined entirely and exclusively by the movement of the molecules (micro level), we don’t need to know the details to predict its value. The details of the micro level seem to disappear at the macro level. This is a typical case of information reduction.

In the next post I’ll make some precisions concerning the waterglass.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 4: Framing

Leave a comment
Framing matters

The framing effect is a topic that comes up a lot these days. Framing is the phenomenon whereby the same message is perceived differently, depending on what additional information is sent with it. The additional information is provided to give the message the right ‘frame’ so that recipients respond appropriately.

Even if the additional information is undoubtedly true, the recipient can be genuinely manipulated by framing, simply by the selection of details that are in themselves factually correct. Framing is, of course, used in advertising, but its role in political reporting has become something of a hot topic of late.

Of course, framing in politics and advertising always involves choosing words that connect an item of information to the corresponding emotional content. But the simple fact that some aspects (details) of events are drawn into the foreground and some pushed into the background changes the image that the recipient forms of the message. For example, our response to the fact that a lot of refugees/migrants want to come to Europe depends on which of the many people we have in mind and which of the diverse range of aspects, reasons, circumstances and consequences of their journey we focus on. Reports about the criminal activities of individual migrants evoke a completely different image from descriptions of the inhuman, unfathomably awful conditions of the journey. That people are coming is a fact. But the way this fact is evaluated – its interpretation – is a matter of simplification, i.e. the selection of data. This brings us clearly to the phenomenon of information reduction.

Framing and information reduction

Real-world situations always contain much more detail than we can process. And because this means we always need to simplify them, information selection plays a crucial role: what do we bring to the forefront and what do we push into the background? The answer to this question colours our perception and thus our opinion. This phenomenon of information reduction is the same as that encountered in medical coding, where a variety of characteristics are drawn upon – or disregarded – in the assignment of codes (see article Two types of coding 1). The reduction and selection of information is part of all perception processes, and our actions and decisions are always based upon simplifications. The selection of details is what shapes our perception, and this selection depends not upon the object being viewed, but on the subject making the selection.

Diverging interpretations are possible (see previous article)

Reality (top of the diagram) is made up of all the facts, but our interpretation of it is always based upon a selection from this vast array of detail. This may lead us to form a range of different opinions. I believe that this phenomenon of information reduction (the interpretation phenomenon) is both fundamental and inescapable, and that it plays an important role in a wide range of different contexts. The framing effect is a typical example, but it is one of many.

Links to framing (in German):
– Spiegel article “Ab jetzt wird zurückgeframt” of 22.2.2019
– Wikipedia.de on the framing effect
– Interview with communication trainer Benedikt Held

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 3: Information is Selection

Leave a comment
Information reduction is everywhere

In a previous post, I described how the coding of medical facts – a process that leads from a real-world situation to a flat rate per case (DRG) – involves a dramatic reduction in the amount of information:

Informationsreduktion

Information reduction

This information reduction is a very general phenomenon and by no means limited to information and its coding in the field of medicine. Whenever we notice something, our sensory organs – for example our retinas – reduce the amount of information we take in. Our brain then simplifies the data further so that only the essence of the impressions, the part that is important to us, arrives in our consciousness.

Information reduction is necessary

If you ask someone how much they want to know, most people will tell you that they want to know as much as possible. Fortunately, this wish is not granted. Many will have heard of the savant who, after flying over a city just once, was able to draw every single house correctly from memory. Sadly, the same individual was incapable of navigating his everyday life unaided – the flood of information got in the way. So knowing every last detail is definitely not something to aspire to.

Information reduction means selection

If it is necessary and desirable to lose data, the next question concerns which data we should lose and which we should retain. Some will imagine that this is a natural choice, with the object we are looking at determining which data is important and which is not. In my opinion, this assumption is simply wrong. It is the observer who decides which information is important to him and which he can disregard. The information he chooses to retain will depend upon his goals.

Of course, the observer cannot get information out of the object that the object does not contain. But the decision as to which information he considers important is down to him – or to the system he feels an allegiance to.

This is particularly true in the field of medicine. What is important is the information about the patient that allows the doctor to make a meaningful diagnosis – and the system of diagnoses depends essentially on what can be treated and how. Medical progress means that the aspects and data that come into play will change over time.

In other words, we cannot know everything, and we must actively reduce the amount of information available so that we can make decisions and act. Information reduction is inevitable and always involves making a choice.

Different selections are possible

Which information is lost and which is retained? The answer to this question determines what we see when we look at an object.

Interpretation der Realität

Various information selections (interpretations) are possible

Because the observer – or the system that he lives in and that moulds and shapes his thinking – decides which information to keep, different selections are possible. Depending on which features we prioritise, different individual cases may be placed in a given group or category and different viewers will thus arrive at different interpretations of the same reality.

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 2: The Funnel

Leave a comment
The funnel of information reduction

In my previous article Information reduction 1, I described a chain of information processing from the patient to the flat rate per case (DRG):

This acts as a funnel, reducing the amount of information available at each step.  The extent of the reduction is dramatic. Imagine we have the patient in front of us. One aspect of a comprehensive description of this patient is their red blood cells. There are 24-30 trillion (= 24–30·1012 ) red blood cells in the human body, each with a particular shape and location in the body, and each moving in a particular way at any given time and containing a certain amount of red blood pigment. That is indeed a lot of information. But, of course, we don’t need to know all these details. As a rule, it is sufficient to know whether there is enough red blood pigment (haemoglobin) in the bloodstream. Only if this is not the case (as with anaemia) do we want to know more. Thus, we reduce the information about the patient, selecting only that which is necessary. This is entirely reasonable, even though we lose information in the process.

The funnel, quantified

To quantify how much information reduction takes place, I have cited the number of possible states at each stage of information processing in the above figure. From bottom to top, these are as follows:

  • DRGs (flat rates per case): There are various DRG systems. However, there are always about 1000 different flat rates, i.e. 103 At the level of the flat rate per case, therefore, 103 different states are possible. This is the information that is available at this level.
  • Codes: In Switzerland, the ICD-10 classification system offers 15,000 different codes Let us assume, as an approximation, that each patient has two diagnoses. So we can choose between 15,000 states twice, giving 225,000,000 = 2.25 x
  • 108
  • .
  • Texts: SNOMED, an extensive medical nomenclature, contains about 500,000 (5 x 105) different expressions. Since a medical record contains a great many words, the amount of information here is naturally much more detailed. My estimate of 1015 is definitely on the low side.
  • Perception and reality: I won’t make an estimate. The above example involving red blood cells illustrates the huge amounts of information available in real-world situations.

Read more in Information reduction 3

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information

Information Reduction 1: Coding

Leave a comment

Two types of coding

In a previous post, I described two fundamentally different types of coding. In the first, the intention is to carry all the information contained in the source over into the encoded version. In the second, on the other hand, we deliberately refrain from doing this. It is the second – the information-losing – type that is of particular interest to us.

When I highlighted this difference in my presentations twenty years ago and the phrase ‘information reduction’ appeared prominently in my slides, my project partners pointed out that this might not go down too well with the audience. After all, everyone wants to win; nobody wants to lose. How can I promote a product for which loss is a quality feature?

Well, sometimes we have to face the fact that the thing we have been trying to avoid at all costs is actually of great value. And that’s certainly the case for information-losing coding.

Medical coding

Our company specialised in the encoding of free-text medical diagnoses. Our program read the diagnoses that doctors write in free text in their patients’ medical records and automatically assigned them a code based upon a standard coding system (ICD-10) with about 15,000 codes (Switzerland, 2019). This sounds like a lot, but the number is small considering the billions of distinguishable diagnoses and diagnostic formulations that occur in the field of medicine (see article). Of course, the individual code cannot contain more information than the standard code is able to discern for the case in question. The full-text diagnoses usually contained more information than this and our task was to automatically extract the relevant parts from the free texts in order to assign the correct code. We were fairly successful in this attempt.

Coding is part of a longer chain

But coding is only one step in a bigger process. Firstly, the information-processing chain extends from codes to flat rates per case (Diagnosis Related Groups = DRGs). Secondly, the free texts to be coded in the medical record are themselves the result of a multi-stage chain of information processing and reduction that has already been performed. Overall, a hospital case involves a chain made up of the following stages from patient examination to flat rate per case:

  • Patient: amount of information contained in the patient.
  • Doctor: amount of information about the patient that the doctor recognises.
  • Medical record: amount of information documented by the doctor.
  • Diagnoses: amount of information contained in the texts regarding the diagnoses.
  • Codes: amount of information contained in the diagnosis codes.
  • Flat rate per case: amount of information contained in the flat rate per case.

The information is reduced at every step, usually quite dramatically. The question is, how does this process work? Can the reduction be automated. And is it a determinate process, or one in which multiple options exist?

This is a page about information reduction — see also overview.

Translation: Tony Häfliger and Vivien Blandford

Information, Semantics

Two Types of Coding 2

Leave a comment
The two types of coding in set diagrams

I would like to return to the subject of my article Two types of coding 1 and clarify the difference between the two types of coding using set diagrams. I believe this distinction is so important for the field of semanticsand for information theory in general, that it should be generally understood.

Information-preserving coding

The information-preserving type of coding can be represented using the following diagram

Mengendiagramm 1:1-Kodierung

Fig 1: Information-preserving coding (1:1, all codes reachable)

The original form is shown on the left and the encoded form on the right. The red dot on the left could, for example, represent the letter A and the dot on the right the Morse code sequence dot dash. Since this is a 1:1 representation, you can always find your way back from each element on the right to the initial element on the left, i.e. from the dot dash of Morse code to the letter A.

Mengendiagramm 1:1-Kodierung, nicht alle Kodes erreicht

Fig. 2: Information-preserving coding (1:1, not all codes reachable)

Of course, a 1:1 coding system preserves information even if not all codes are used. Since the unused ones can never arise during coding, they play no role at all. For each element of the set depicted on the right that is used for a code, there is exactly one element in the initial form. The code is therefore reversible without loss of information, i.e. decodable, and the original form can be restored without loss for each resulting code.

Mengendarstellung: Informationserhaltende Kodierung (1:n)

Fig. 3: Information-preserving coding (1:n)

With a 1:n system of coding, too, the original form can be reconstructed without loss. An original element can be coded in different ways, but each code has only one original element. There is thus no danger of not getting back to the initial value. Again, it does not matter whether or not all possible codes (elements on the right) are used, since unused codes never need to be reached and therefore do not have to be retranslated.

For all the coding ratios shown so far (1:1 and 1:n), the original information can be fully reconstructed. It doesn’t matter whether we choose a ratio of 1:1 or 1:n, or whether all possible codes are used or some remain free. The only important thing is that each code can only be reached from a single original element. In the language of mathematics, information-preserving codes are injective relations.

Information-reducing coding
Mengendiagramm: Informationsreduzierende Kodierung

Fig. 4: Information-reducing coding (n:1)

In this type of coding, several elements from the initial set point to the same code, i.e. to the same element in the set of resulting codes. This means that the original form can no longer be reconstructed at a later time. The red dot in the figure on the right, for example, represents a code for which there are three different initial forms. The information about the difference between the three dots on the left is lost in the dot on the right and can never be reconstructed. Mathematicians call this a non-injective relation. Coding systems of this type lose information.

Although this type of coding is less ‘clean’, it is nevertheless the one that interests us most, as it typifies many processes in reality.

Information, Semantics

Two Types of Coding 1

Leave a comment
A simple broken bone

In the world of healthcare, medical diagnoses are encoded to improve transparency. This is necessary because they can be formulated in such a wide variety of different ways. For example, a patient may suffer from the following:

– a broken arm
– a distal radius fracture
– a fractura radii loco classico
– a closed extension fracture of the distal radius
– a Raikar’s fracture, left
– a bone fracture of the left distal forearm
– an Fx of the dist. radius l.
– a Colles fracture

Even though they are constructed from different words and abbreviations, all the above expressions can be used to describe the same factual situation, some with more precision than others. And this list is by no means exhaustive. I have been studying such expressions for decades and can assure you without any exaggeration whatsoever that there are billions of different formulations for medical diagnoses, all of them absolutely correct.

Of course, this  huge array of free texts in all variations cannot be processed statistically. The diagnoses are therefore encoded, often using the ICD (International Classification of Diseases) system, which comprises between 15,000 and 80,000 different codes depending on variant. That’s a lot of codes, but much clearer than the billions of possible text formulations it replaces.

Incidentally, the methods used to automate the interpretation of texts so that it can be performed by a computer program are a fascinating subject.

Morse code 

Morse code is used for communication in situations where it’s only possible to send very simple signals. The sender encodes the letters of the alphabet in the form of dots and dashes, which are then transmitted to the recipient, who decodes them by converting them back into letters. An E, for example, becomes a dot and an A becomes a dot followed by a dash. The process of encoding/decoding is perfectly reversible, and the representation unambiguous.

Cryptography

In the field of cryptography, too, we need to be able to translate the code back into its original form. This approach differs from Morse code only in that the translation rule is usually a little more complicated and is known only to a select few. As with Morse code, however, the encrypted form needs to carry the same information as the original.

Information reduction

Morse code and cryptographic codes are both designed so that the receiver can ultimately recreate the original message. The information itself needs to remain unchanged, with only its outer form being altered.

The situation is quite different for ICD coding. Here, we are not dealing with words that are interchangeable on a one-for-one basis such as tibia and shinbone – the ICD is not, and was never intended to be, a reversible coding system. Instead, ICD codes are like drawers in which different diagnoses can be placed, and the process of classification involves deliberately discarding information which is then lost for ever. This is because there is simply too much detail in the diagnoses themselves. For example, a fracture can have the following independent characteristics:

– Name of the bone in question
– Site on the bone
– State of the skin barrier (open, closed)
– Joint involvement (intra-articular, extra-articular)
– Direction of the deformity (flexion, extension, etc.)
– Type of break line (spiral, etc.)
– Number and type of fracture fragments (monoblock, comminuted)
– Cause (trauma, tumour metastasis, fatigue)
– etc.

All these characteristics can be combined, which multiplies the number of possibilities. A statistical breakdown naturally cannot take all combination variants into account, so the diagnostic code covers only a few. In Germany and Switzerland, the ICD can cope with fewer than 20,000 categories for the entire field of medicine. The question of what information the ‘drawers’ can and cannot take into account, is an important topic both for players within the healthcare system and those of us who are interested in information theory and its practical application. Let’s turn now to the coding process.

Two types of coding

I believe that the distinction described above is an important one. On the one hand, we have coding systems that aim to preserve the information itself and change only its form, such as Morse code and cryptographic systems. On the other hand, we have systems such as those for encoding medical diagnosis. These aim to reduce the total amount of information because this is simply too large and needs to be cut down – usually dramatically – for the sake of clarity. Coding to reduce information behaves very differently from coding to preserve information.

This distinction is critical. Mathematical models and scientific theories that apply to information-preserving systems are not suitable for information-reducing ones. In terms of information theory, we are faced with a completely different situation.

Logic

Non-Monotonic Reasoning (NMR)

Leave a comment

Concept Molecules and NMR

In the article Two types of coding 1, I described the challenge of getting computers to ‘understand’ the incredibly diverse range of medical diagnoses that may crop up in a text. To meet this challenge, the computer has to convert the various diagnostic formulations encountered into a consistent format that represents all the semantic details in an easily retrievable form.

With concept molecules we have succeeded in doing this. We were aided here by two properties of the concept molecules method:
a) the consistently composite representation of semantics, and
b) a non-monotonic reasoner.
At the time, the use of a non-monotonic reasoner was very much out of vogue. Most research groups in the field of medical computational linguistics were in the process of switching from First Order Logic (FOL) to Description Logic (DL), believing that DL is the best way to get computers to interpret complex semantics. As it turned out, however, it was us – a small private research company without state support – that was successful. Instead of the accepted doctrine of FOL and DL based upon a monotonic approach, we used a non-monotonic method.

What is monotonic logic?

In logic, monotony means that the truth of statements does not change even if new contradictory information subsequently crops up. Thus, what has been recognised within the system as true remains true, and what has been recognised as false remains false. Under non-monotony, on the other hand, conclusions drawn by the system can be called into question on the basis of additional information.

So, what’s the problem with non-monotony?

It is clear that proof is only possible in a monotonic system. In a non-monotonic system, on the other hand, there is always the possibility of another argument cropping up that leads to completely different conclusions. Since proof is essential in mathematics, it is obvious that mathematical logic relies on monotony.

Computational linguistics, however, is not about proof, but about the correct assignment of words to concepts. Thus, the advantage of being able to supply proof – as important as it clearly is for mathematics – is irrelevant to our task.

And the problem with monotony?

A system that cannot change its conclusions is not able to learn in any real sense. The human brain, for example, is in no way monotonic.

Moreover, a monotonic system must also be closed, whereas in practice scientific ontologies are not closed, but grow as knowledge progresses. Progress of this kind is also evident in the development of an interpretation program with its complex algorithms:  here, too, there is continuous improvement and expansion that poses problems for monotonic systems.

In addition, monotonic systems are not particularly efficient when it comes to dealing with exceptions. It is well known that there are exceptions to every rule, and a non-monotonic system can handle these in a much more effective and straightforward way.

Non-monotony in practice

If we compare rules-based systems, I believe that non-monotonic systems are clearly preferable to monotonic ones for our purposes. Non-monotony is by no means the easy option and has a few pitfalls and knotty issues of its own, but the ease with which even detailed and complex fields can be modelled decides the issue in its favour.

Information

What Information does a Bit Convey?

Leave a comment

What does a bit mean?

The question may seem trivial – after all, everyone knows that a bit represents a choice between 0 and 1. Isn’t it?

So, what’s the problem?

The problem is that 0 and 1 are not the only answers. 0 and 1 are just a pair of possible instantiations for a bit, especially useful if you look at numbers, but there are many more possiblities.

Classic examples are:

– yes and no
– true and false
– positive and negative
– on and off

to name but a few. Other options include male/female, inside/outside, good/bad and any other binary pair you care to think of, as well as the associated inversions: for example, 1/0 as well as 0/1.

Bits select information. This information can be numbers, but information encompasses much more than numbers. Laymen think that bits are based on 0 and 1, but 0 and 1 are only a possible instatiation of something more general, namely information.

How does the bit know which two states it can represent?

You may think that the quality of information (like number count, truth value, positivity, direction etc) is an inherent property of the bit itself, with one bit representing 0/1 and another one representing for example true/false. This is not the case. Chip manufacturers do not assign individual properties to the bits within their chips in this way. From a technical point of view, all bits are identical, and it is precisely this simplicity and neutrality that makes binary, i.e. bit technologies so attractive.

Only when the computer runs a program do the previously neutral bits take on individual value pairs such as 0/1, true/false, etc. It is thus the program that assigns a meaning to the two states of the bit.

Of course, this has practical benefits because it means that the meaning assigned to a particular bit within a chip can be redefined time and time again, depending what program happens to be running. But it also means we have to face the fact that this meaning is not an inherent property of the bit itself, but a function of the program that calls it up, and thus of different bits entirely – those of the program.

But where do these bits take their meaning from? Of course, these bits also have value pairs assigned to them from the outside in exactly the same way. And so it goes on, with the meaning of value pairs always being assigned from the outside by other bits. In other words, this is an infinite regress in which every bit that explains another bit itself has to be explained by yet another.

Where does the chain end?

This search for the bits that explain other bits never ends; that is the nature of an infinite regress. But we do still have a chance of finding the end of the chain: the search is only hopeless as long as we remain within the confines of the computer. Human beings, however, can think beyond these limits. The program was written for a certain purpose and it is human beings – programmers and users – who decide what meaning they want the bits to have. This meaning, and thus the specific individual value pairs assigned to the bits, emerges offline at the end of the regress as an implicit understanding in the minds of human beings.

This has taken us beyond the world of bits, and I would argue that this is unavoidable: until we escape these bounds, we remain in a world that is precise but completely devoid of meaning. Individual bits only take on meaning when this is assigned from the outside, i.e. when we link them to information that is meaningful to us as human beings. This allows us to resolve the infinite regress.

Seen in isolation, the two states of the bit are completely neutral, which means we can assign them any meaning we like. Technically, that’s a stroke of genius. But we shouldn’t deceive ourselves that we can generate meaningful information from bits alone. There always needs to be an ‘outside’ that assigns meaning to the bits.

We thus have two types of information:

1. The isolated bit:

This indicates which of the two states of the bit is selected without describing the states themselves. It is the ‘technical’ bit of information theory.

2. The meaning assigned to the bit:

This tells us what the bit is all about, i.e. which two states it allows us to choose between. This is the qualitative information that can be expressed using the bit. Although we assign this information to the bit itself, it disappears as soon as we look at the bit in isolation.

These two types of information are fundamentally different.

Despite – or maybe precisely because of – this difference, they belong together. It is only by their combination that meaningful information is produced.

D. M.  MacKay: Selective and descriptive information content

Following the information science pioneer D. M. MacKay, we can call the two types of information the selective and the descriptive information content.