The fifth
Let us first have a look at the fifth. It is a feature of practically all the musical scales of human cultures. Musical scales without this pure fifth do exist, but these musical scales strike me either as artificial and deliberately designed like the whole tone scales or rather uncommon like the Locrian mode. The blues scale makes use of the “blues note” – the “flat five”, a note close to the fifth known as the diminished fifth – but also uses the perfectly normal fifth. After the octave, the fifth is certainly the interval that occurs most frequently in all the thousands of musical scales on this earth.
Fifth and twelfth
Can this normal fifth be generated by resonance like the octave? Although it is not an overtone, it can still be reached through the overtones. Below, I will show how this works, namely with a short detour through the twelfth, the third overtone.
The graph with the vibrating overtones will serve to illustrate this:
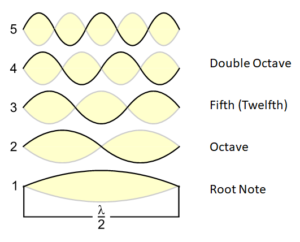
Fig. 1: A vibrating string with the fundamental tone and the first four harmonics (overtones)
In Fig. 1 I have even described the third overtone as a fifth, which is actually wrong, for in reality it is a twelfth. Nonetheless, this tone immediately strikes us as a fifth when we hear it. In Fig. 2, you can see an example of fifths and twelfths on a piano keyboard:
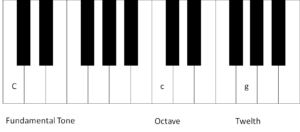
Fig. 2: Octave and twelfth on the piano
In our example, the fundamental tone is a (capital) C. The first overtone, the octave, is a (small) c and the second overtone, the twelfth, a (small) g. In relation to the fundamental tone C, the small g is a twelfth, but in relation to the first overtone, i.e. the small c, the g is a fifth.
The frequency of the fifth
What about this c-g interval in terms of frequency? To find out, let us compare Figures 1 and 2: Tone 3 (g) is three times the fundamental vibration (C) and tone 2 (c) twice the fundamental vibration. Thus tone 3 (g) vibrates 3/2 times as fast as tone 2 (c). If we take the small c rather than the capital C as the fundamental tone, then the small g is the fifth. And in the fifth, the upper tone (g) vibrates 3/2 times as fast as the lower tone (c). This is generally applicable:
A tone which vibrates 3/2 times as fast as another sounds a fifth higher to us.
The three worlds in the fifth
The fraction 3/2 is the mathematical aspect of the fifth. We have deduced it through the physics of the string vibrations. At the same time, we complied with the previously mentioned conditions (constraints) from the mental world: if the quint is meant to be a tone of a musical scale, it must not be too far away from the fundamental tone. This applies to every tone of a musical scale; it must be within an octave. In mathematical terms, this means that the ratio between its frequency and the frequency of the fundamental tone must be between 1 (= fundamental tone) and 2 (= octave). The fifth satisfies this requirement with the frequency ratio of 3/2 = 1.5. In the case of the twelfth, the frequency ratio is 3, i.e. greater than 2, and thus the twelfth is not a note of the musical scale. We perceive it as a fifth, but as mentioned before, in the mental world we perceive the octave as the “same” tone.
The resonance experiment for the fifth
To illustrate the relationship between the fundamental tone, the fifth and the twelfth, I propose a further resonance experiment on the piano:
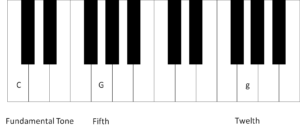
Fig. 3: Resonance experiment for the fifth. In comparison to Fig. 2, the key on which we investigate the resonance is now the fifth – the capital G – and not the small g.
To begin with, we again test the twelfth and press the twelfth (the small g) with the right hand like in the octave experiment . The string should not make a sound, but the key must be kept depressed. With the left hand, we briefly and vigorously hit the C, i.e. the fundamental tone. Like in the octave experiment, the depressed string (g) should make a sound although it was not hit. This is pure resonance; the string makes a sound because it was stimulated by sound waves. This works because the small g is an overtone of the capital C.
But what about the capital G, i.e. the fifth? To test this, keep the capital G mutely depressed while vigorously hitting the fundamental tone, i.e. the capital C. You can now hear a high tone. If you listen carefully, you will notice that this is not the fifth, i.e. the capital G, but the twelfth, i.e. the small g. How come this tone sounds although you don’t keep the key of the small g depressed at all?
In fact the sound of the small g is produced on the string of the capital G! This means that the string does not vibrate in its fundamental vibration but in its first upper vibration, the octave. This works well because the string can vibrate almost as well with two antinodes (bellies) as with one. This is the so-called flageolet-note.
In other words: you have stimulated a harmonic on the string whose frequency is twice the speed of the fundamental frequency of the string. But where did the stimulus for this frequency come from? – It is the capital C string which initiated the overtone. The vibration of this C string contains the small g as a harmonic, namely the second overtone. This second overtone stimulates the (capital) G string to resonate, but not with its fundamental vibration (G), but with its first overtone, the small g, for only this can be stimulated as a harmonic of the (capital) G string. You can hear this tone (g) on the G string as long as you keep the G key depressed.
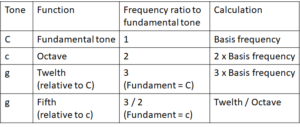
Table 1: The resonance of the fifth
Thus the resonance of the fifth is generated by the detour of the overtones. Neither string is involved in its fundamental vibration, but both strings are involved through their harmonics. The fact that this works has been demonstrated with the fifth experiment.
The fifth, a simple fraction
In Table 1, the fifth is represented as a fraction: 3/2.
As we have seen, all the tones of a musical scale must be within the range of an octave, i.e. their frequency must be between the single value and the double value of the frequency of the fundamental note. This has been achieved with the frequency ratio of 3/2 = 1.5. We have thus found the first tone within the octave range which has a very simple interval relation to the fundamental note. Whereas the octave vibrates at twice the speed of the fundamental note, the fifth vibrates 3/2 times as fast.
With the exception of the octave, the overtones do not fulfil the conditions for musical scales. Nonetheless, they play a role as transmitters of resonance. We have produced the fifth by simply breaking down the twelfth (the second overtone) by one octave. This breaking down by an octave manifests itself as the 2 in the denominator. The 3 in the numerator is the “inheritance” of the second overtone, the twelfth, which vibrates at three times the rate of the fundamental tone.
Summary
With the fraction of 3/2, which defines the fifth, we have obtained a strikingly simple ratio. This is no accident. We will see how these simple ratios (ideal world!) also play a part for the other notes of a musical scale.
The fact, however, that we are no longer able to use ratios of single integers, like with the overtones, for the musical scales and that instead, fractions (of two integers) are used, is due to the constraint of the octave limitation, which is a constraint of the physical/mental world.
The fifth is not the sole fraction among our musical scale intervals. Integer fractions define the most important tone intervals. We can find them with a simple design rule. On the following page, I will show how this design rule works.
This is a post about the theory of the three worlds.