The major scale
The major scale (Ionian mode) is the most widespread musical scale both in Europe and globally. It is a heptatonic scale, i.e. a musical scale with seven tones. It is characterised by very special resonance ratios, which serve well to explain its worldwide appreciation.
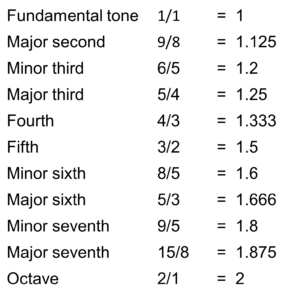
Below, I have listed the tones of the major scale of C, ascending from the bottom to the top, together with the intervals between each tone and the fundamental tone. Of course, it is these intervals that constitute the musical scale. We could also start the musical scale with any other tone and only speak of the intervals (second, third, etc.) since we only need the distances between the tones to describe a musical scale. However, I am using the tone of the C major scale, simply because it is clearer and also enables you to reproduce it more easily on a piano or other instrument.
The interval designates the ratio of the frequency of a scale tone to the frequency of the fundamental tone. This interval always lies between 1 (fundamental tone) and 2 (octave) in every musical scale. We express it in the form of a fraction.
C 2
B 15/8
A 5/3
G 3/2
F 4/3
E 5/4
D 9/8
C 1
Table 1: The C major scale
The fractions enable us to recognise what is typical of the major scale. It can be shown very well that what we hear subjectively (mental world) is perfectly in parallel with what we are able to represent mathematically in simple fractions (Platonic world). It turns out again that the three worlds (according to Penrose) interact perfectly in the field of music.
All the tones resonate with the fundamental tone
In a previous post, I established resonance criteria for scale tones. These criteria yield ten tones which strongly resonate with the fundamental tone. Like the standard pentatonic scales, the major heptatonic scale consists of a selection of these ten most resonant tones. Thus we may assume that the major scale is generally strongly resonant in itself. Yet not every tone is equally resonant with the fundamental tone. And among themselves, in particular, tones resonate very differently. This is where the story becomes interesting. To begin with, we’ll have a look at the difference between the major heptatonic scale and the major pentatonic scale.
The major heptatonic scale as an extension of the major pentatonic scale
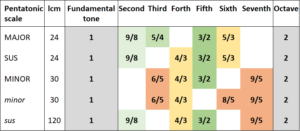
The standard pentatonic scales are the most strongly resonant musical scales in general, and the most resonant of them is the major pentatonic scale. The major heptatonic scale can be regarded as an extension of the major pentatonic scale. Both musical scales are subsets of the ten most resonant tones.
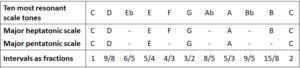
Table 2: Comparison between the major pentatonic and the major heptatonic scales
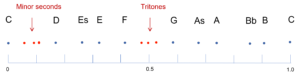
The tones which are added to the heptatonic scale in comparison with the pentatonic scale explain the difference. Whereas the pentatonic scale is resonant throughout and all tones can be mixed at random without any tensions occurring, this is no longer the case with the heptatonic scale. The two additional tones, F and H, introduce the necessary tension for the matter to become interesting.
The first thing that strikes us is the fact that with H, that tone is added which among the ten most resonant tones has the highest digits in the numerator and the denominator. Among the ten most resonant tones, it is therefore the tone that resonates most poorly with the fundamental tone, the tone that creates most tension. This concerns its relation to the fundamental tone.
However, the intervals between different scale tones apart from the fundamental tone play a role in musical scales, too. We calculate this by dividing the frequency ratio of the upper tone by that of the lower tone (for the reasons for dividing, cf. Appendix). The two new additional tones in the heptatonic scale, i.e. F and B, generate a tension both mathematically and audibly such as has not occurred in the pentatonic scales so far. If, for instance, we sound F together with E, then this results in a frequency ratio of 4/3 : 5/4 = 16/15, a fraction which indicates a resonance that is difficult to achieve. H and the upper C sounded together have a similar result; here, the ratio is 2/1 : 15/8 = 16/8 : 15/8 = 16/15. Thus the interval between H and C is as full of tension as that between E and F. The interval between F and H is even more critical; here, the fraction is 15/8 : 4/3 = 45/32. These are two high numbers indeed, compared to what we have seen before, and they offer no possibility of reducing.
Tension and easing
Poor resonance means tension since both tones do not easily go together. We apprehend this subjectively (mental world), as you can easily find out by striking an E and an F at the same time on the piano and comparing the sound with the simultaneous sounding of, say, E and G. E and F produce more friction. Physically, the mathematics of the frequency ratios express a lesser or higher degree of readiness to enter into a resonant relationship, and we can hear this.
Musically, however, tension is not without interest. The major pentatonic scale without F and H may strike us as quiet and harmonious, but also as a bit dull. Conversely, the major heptatonic scale contains little peppercorns which introduce an exciting pungency, similarly to the hotness of chilli peppers in a dish. Yet whereas you can still feel this hotness as a long aftertaste, this pungency in music can be switched on and off with precision by simply replacing the tone that creates tension with a quiet one that resonates without any problem. This interplay of tension and easing is extensively used in music.
The major heptatonic scale as a subset of the ten most resonant tones
As illustrated in Table 2, the major scale is a selection of seven tones from the list of the ten most resonant tones. This selection packs a punch. I will shortly deal with the mathematical details which result from it. You will probably not be surprised that these mathematical details are again in parallel with our listening experience. Let’s first look at which of the ten tones are missing in the major scale: they are Eb, Ab and Bb. As always, we look at the fractions of these three intervals: 6/5, 8/5 and 9/5. We quickly notice that all these fractions have the denominator 5. Conversely, none of the tones in the major heptatonic scale do have the denominator 5.
Reducing the denominator
This fact of the missing denominator 5 facilitates the resonances within the major heptatonic scale. If two tones have the same denominator, this is cancelled out when we sound the two tones simultaneously. If, conversely, there are different denominators, resonance will be made more difficult. Different denominators, however, can be reduced too, if they can be divided by each other.
For this purpose, we conduct an integer factorisation. In the major scale, for example, the major seventh and the major third resonate perfectly with each other: in order to calculate the resonance mathematically, we divide the major seventh by the major third, which results in 15/8 : 5/4 = 3/2. These 3/2 luckily indicate a perfectly resonant interval, namely the fifth.
The cancelling in this case is possible because in integer factorisation, both the denominator 8 and the denominator 4 contain the prime number 2 twice (8=2×2×2 und 4=2×2). Thus the factor 2 can be cancelled out (even twice, since both denominators contain it twice). This cancelling (reducing) can be done whenever two numerators contain the same factors.
For this reason, it is “clever” of the major scale to omit precisely all the tones with the denominator 5. In this way, the 5 never intrudes, and reductions are more easily possible. And reduced fractions with regard to the frequency ratios mean better resonance both physically and mentally.
The resonance of the totality of all scale tones together
We can roughly estimate the reduction behaviour of the totality of all the tones in a musical scale by calculating the lcm (least common multiple) of all the denominators, as we already did with the pentatonic scales. The tones of the major heptatonic scales have an almost unbeatable lcm of 24; it is even the same as that of the major pentatonic scale with two fewer tones.
This low lcm is of course the result of the fact that there aren’t any tones with the denominator 5 in the scale; otherwise we would have to multiply the lcm by 5, which would result in 120.
The lcm is useful but does not say everything
However, the lcm doesn’t show the whole resonance behaviour of the musical scale. It is only a measure for the resonance of all the scale tones with the fundamental tone, but does not say anything about how the scale tones resonate with each other. For the above-mentioned interval of the tones F and B, for instance, we obtain a frequency ratio of 45/32, which means that even if the tones resonate well with the fundamental tone, they can be full of tension among themselves.
This is not a weak point, though; rather, it makes the musical scale interesting. In this respect, the major heptatonic scale is clearly more interesting than the major pentatonic scale although both of them have the same lcm.
Nonetheless, the lcm is a valuable yardstick against which the basic resonance potential in the musical scale can be roughly measured, since with a high lcm, i.e. when the denominators cannot be reduced, the dissonances are sharper in any case.
Triads in the major scale
We now turn our resonance considerations to three tones that are sounded simultaneously. Let us analyse the triad of C, E and G. The frequencies (cf. Table 1) are: 1 – 5/4 – 3/2. To calculate the ratio of all three tones to each other, we must place all three of them on the same denominator. It is precisely for this that we need the lcm again, which in this case is 4. Thus 1 – 5/4 – 4/2 results in a ratio of 4/4 – 5/4 – 6/4. The common denominator can be cancelled out, and the ratio of the frequencies of C-E-G is 4 – 5 – 6.
This is absolutely the most resonant ratio which is possible when three different tones are sounded together. The C-E-G triad is the major triad with which everyone is familiar. On the piano, it is slightly distorted due to temperament, but even so you can easily try out for yourself how catchy and attractive this triad is. No wonder it plays such a dominant role in pop and folk music.
Three major triads in the major heptatonic scale
However, the major heptatonic scale does not contain the major triad only once, but three times. Look at the tones F – A – C, in fractions 4/3 – 5/3 – 2, or all the tones placed on the common denominator 3: 4/3 – 5/3 – 6/3, i.e. again 4 – 5 – 6. This demonstrates once more the benefit which the common denominator (here: 3) represents for the resonances. Thus the major heptatonic scale did well to include the tone of F, which allows for a second major triad.
But H is also well chosen, for it enables a third major triad in the major heptatonic scale. This time, we start with G and add H. As a third note, we take D, an octave higher than usual, i.e. just above the upper C. For this purpose, we have to multiply the 9/8 of D by 2, which results in 9/4 (cf. calculation rules). This fraction is higher than 2, i.e. is already above the octave. Let us now look at the tones G – H – D; the frequencies are 3/2 – 15/8 – 9/4. With the lcm=8, we obtain 12/8 – 15/8 – 18/8. We can now reduce the numerators and denominators, which again results in 4 – 5 – 6, i.e. the same ratio as above, the same perfectly resonant major triad as those with the roots C or F.
Thus the major heptatonic scale contains the major triad no fewer than three times, for three tones of the heptatonic scale can be combined in this most resonant manner three times. What is also remarkable, however, is the fact that the three triads do not mix very well with each other. This is easily heard; again, the mathematics perfectly corresponds to our subjective mental experience (sorry, I have to mention this thing with the three worlds again and again; I myself am surprised how well they converge in musical scales).
Of course, the major scale was not “invented”, and certainly not by a mathematician. Rather, this musical scale was found by people who themselves actively made music and thus became aware of the particularly interesting resonance relationships which result from the combination of tones.
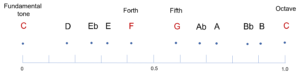
As we just have seen, there are three independent collections of tones inside the major scale which resonate well within themselves but harmonise less well with the other selections. This results in three different colours or harmonies inside the major scale which can be used separately and whose sequence can be planned in a piece of music and thus tells us a story. The three colours are defined by the root of each triad, namely by the fundamental tone of the musical scale (C), its fourth (F) and its fifth (G). The three tones are called tonic (fundamental tone), subdominant (fourth) and dominant (fifth). The possibility of playing with such colour far exceeds the possibilities of the major pentatonic scale and was studied and perfected in Europe throughout the course of the centuries.
Minor triads
These triads, too, have a special resonance ratio, namely 10 – 12 – 15. The numbers are slightly higher than in the major triad, which makes the minor triad slightly less resonant. For three different tones, however, the ratio is still extremely simple and thus resonant, and minor triads are certainly not dissonances.
In the minor triad, the minor third is the first tone with a frequency ratio with the denominator 5, whereas the major scale does not have this and prefers denominators based on the prime number 2. This produces a distinctly different colour. With the denominator 5, we have already reached the highest “permitted” prime number, much higher than 2 and its easily divisible multiples found in the major scale. The minor scale therefore sounds softer, more special and not as as the major scale.
The minor triads cannot only be found in the minor heptatonic scale but also in the major heptatonic scale, simply based on less prominent scale tones, specifically on D, E and A. In principle, minor colours can also be produced in the major scale, even though only on less prominent tones.
Conclusion
All in all, the seven tones of the major scale constitute an almost inexhaustible source of combinations. The major scale combines a maximum degree of resonance with the possibility of generating tension and different colours. All this can be easily reconstructed by means of simple mathematical fractions – in complete harmony with what we hear subjectively.
To continue, we will have a look at the Pythagorean comma. This is particularly interesting because it shows how the mathematical world reaches its limits in the physical world. This fact has resulted in an evenly tempered intonation, an “impure” intonation. So have a look at how the Pythagorean comma emerges.
This is a post about the theory of the three worlds.