Resonanz funktioniert über gemeinsame Obertöne
Resonanz besteht, wenn zwei schwingungsfähige physikalische Träger gemeinsam schwingen. Dabei kommt es auf die Eigenfrequenz der beiden Träger an:
- Resonanz 1. Grades: Beide Träger schwingen in der gleichen Frequenz (f2 = f1)
- Resonanz 2. Grades: Ein Träger schwingt in einer Obertonfrequenz des anderen (f2 = n * f1)
- Resonanz 3. Grades: Beide Träger schwingen in einer gemeinsamen Obertonfrequenz (f2 = n/m * f1)
Die Resonanz 3. Grades zeigt sich dadurch, dass das Verhältnis der beiden Frequenzen einem Bruch mit ganzen Zahlen (n/m) entspricht. Diese Resonanz 3. Grades ist die, die uns interessiert, denn sie ist für Tonleitern und Akkorde wirksam, und nicht wie oft angenommen diejenige 2. Grades (siehe den diesbezüglichen Vorbeitrag).
Beispiel Quinte
Eine Saite a' habe die Grundfrequenz 440 Hz und eine Saite e" die Frequenz 660 Hz. Dann schwingt auf der Saite a' der zweite Oberton mit 3 x 440 = 1320 Hz und auf der Saite e" der erste Oberton mit der Frequenz 2 x 660 = 1320 Hz. Dieser Ton ist der gemeinsame Oberton.
Die Saite a' kann nun die Saite e" über diesen gemeinsamen Oberton die Saite anregen. Das Verhältnis der beiden Grundfrequenzen ist entsprechend 3/2.
These
Damit Resonanz entsteht, müssen die Frequenzen im Verhältnis eines Bruchs mit ganzen Zahlen sein.
Warum ganze Zahlen?
Im Schwingungsmedium (Saite, Basilarmembran, etc.) entstehen bei einer Schwingung stehende Wellen. Diese sind dadurch charakterisiert, dass die Saite an ihren beiden Enden nicht schwingt, sondern nur in der Mitte, mit einem oder mehreren Bäuchen. Die Zahl der Schwingungsbäuche in der Mitte muss eine ganze Zahl sein, da sonst die stehende Welle an den beiden Enden nicht auf der Nulllinie wäre.
Tonleitertöne bewerten anhand der Resonanzen
Oktaven und Quinten lassen sich, wie wir hören können, sehr leicht in Resonanz bringen (Quintenexperiment) und zeichnen sich durch sehr einfache Resonanzverhältnisse (f2/f1) aus, nämlich 2/1 für die Oktave und 3/2 für die Quinte. Mit ganz wenigen mathematischen Bedingungen lassen sich nun weitere Tonleitertöne finden:
Kriterien für die Töne einer Tonleiter
Es wird jeweils das Intervall des Tons zum Grundton der Tonleiter angesehen.
- Das Intervall muss innerhalb einer Oktave liegen: Das heisst, der Bruch der beiden Frequenzen (Tonleiterton zu Grundton) muss ≥ 1 und ≤ 2 sein.
- Das Intervall muss resonanzfähig sein: Nenner und Zähler des Bruchs müssen ganze Zahlen sein.
- Die Resonanz soll möglichst kräftig sein: Der Nenner des Bruchs soll möglichst klein sein.
Die beiden letzten Kriterien sind entscheidend, aber etwas erklärungsbedürftig und ich werde gerne die Gründe dafür veranschaulichen. Im Moment aber nehme ich alle drei mathematischen Kriterien als gegeben an und schaue, ob wir damit weitere bekannte Intervalle finden können.
Generierung eines Pools möglicher Tonleitertöne mit Hilfe dieser drei Kriterien
Wir gehen von den Nennern aus und starten dabei mit den Nennern 1 und 2. Bereits enthalten in unserer Tonleiter sind:

Alle übrigen Töne mit Nenner 1 oder 2 liegen ausserhalb unseres Oktavbereichs (1-2). Wir schauen deshalb, ob sich mit dem Nenner 3 weitere bekannte Intervalle ergeben:

Alle weiteren Brüche mit Nenner 3 liegen ausserhalb unseres Oktavbereichs. Wir fahren deshalb mit dem Nenner 4 weiter:
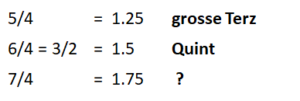
Alle weiteren Brüche mit Nenner 4 liegen ausserhalb unseres Oktavbereichs. Wir fahren deshalb mit Nenner 5 weiter:

Weitere Brüche mit Nenner 5 liegen ausserhalb unseres Oktavbereichs.
Zwischengedanke
Was hier auffällt ist, dass Brüche mit Zähler 7 bei uns in Europa als Intervalle nicht vorkommen. Meine These ist, dass das damit zu tun hat, dass sieben eine Primzahl ist. Das kann erklären, weshalb 8/5 und 9/5 für uns gewohnte Intervalle sind, obwohl Nenner und Zähler bei diesen Brüchen höher ist als bei 7/5. Acht ist 2x2x2 und Neun ist 3×3. Wir werden später sehen, dass wir zur Beurteilung der Resonanz von mehreren Tönen auch mehrere Intervalle miteinander vergleichen können. Zwei Intervalle vergleichen bedeutet in der Frequenzanalyse, dass der Bruch des einen Intervalls durch den Bruch des anderen geteilt wird. Dabei ist es vorteilhaft, wenn gekürzt werden kann. Bei einer Primzahl besteht diese Möglichkeit nicht, bei Zahlen wie 8 oder 9 ist das Kürzen aber oft möglich, insbesondere wenn wir mit Quinten und Quarten das 2 und das 3 im Nenner haben. Beispiele werden folgen.
Für unsere Generierung resonanter Tonleitertöne folgt aber, dass wir auf 7/4 und 7/5 verzichten – weil die 7 im Zähler eine zu hohe Primzahl ist.
Weiter geht es nun mit Nenner 6:

Der Nenner 6 bringt also keine neuen Töne.
Nenner 7 lassen wir als hohe Primzahl weg und gehen gleich zu Nenner 8:

Mit Nenner 8 gibt es somit zwei neue Intervalle, nämlich die grosse Sekunde (9/8) und die grosse Sept (15/8). Zwar sind bei beiden die Zähler und Nenner recht hoch, doch dafür lassen sich ihre Zähler und Nenner durch 2, 3 und 5 teilen. Dadurch werden die Brüche der Intervalle im Verbund von Tonleitern und Akkorden kürzbar und die Intervalle erweisen sich als resonant.
Damit beenden wir die Tonsuche und stellen unsere Funde in aufsteigender Frequenz zusammen:
Pool der resonanzmässig vorteilhaften Intervalle
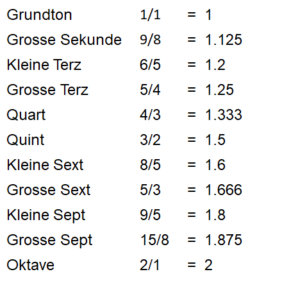
Bei unserem Pool fällt folgendes auf:
a) Die meisten bei uns verwendeten Intervalle haben ganz einfache Frequenzverhältnisse.
b) Die Quart ist mit tiefem Nenner und Zähler der «viert-logischste» Tonleiterton. Dieser Ton ist aber nie ein Oberton. Trotzdem macht er Sinn und zwar sowohl in der mathematischen Welt (einfacher Bruch), wie in der physikalischen Welt (einfache Resonanzverhältnisse) wie auch mental (subjektives, musikalisches Hörerlebnis).
c) Kleine Sekunde und Tritonus fehlen in unserem Pool. Diese Töne sind mathematisch keine problemlosen Brüche und klingen entsprechend schärfer. Das ist musikalisch natürlich interessant, doch das Ideal einer problemlosen Resonanz wird mit diesen Intervallen verfehlt. Wir werden später sehen, wie der Tritonus sich unter gewissen Bedingungen trotzdem gut in Resonanzen einfügen lässt, die kleine Sekunde hingegen klingt immer scharf und wird dadurch der eigentliche Leitton in der europäischen Musik.
Doch vorerst belassen wir es bei unserem Pool von zehn Tönen. Das reicht für viele, insbesondere für die global am häufigsten verwendeten Tonleitern. Wir haben gesehen, dass das mathematische Kriterium eines Bruchs mit kleinen ganzen Zahlen ausreicht, diesen Pool von resonanten Tonleitertönen rein rechnerisch zu generieren und ihn auf nur 10 Töne zu beschränken. Alle diese rein mathematisch definierten Tonleitertöne sind für unsere Ohren (mentale Welt) keine Unbekannten. Das mathematische Kriterium läuft perfekt parallel zu dem, was wir hören.
Weitere Zwischengedanken
Mathematiker mögen bekanntlich Primzahlen. In dieser Hinsicht können wir das oben genannte 3. Kriterium (möglichst tiefe Zahlen für Zähler und Nenner) präzisieren:
3. Kriterium präzisiert:
Damit das Intervall im Verbund mit anderen Intervallen gut resonanzfähig ist, soll Zähler und Nenner bei der Primzahlzerlegung möglichst kleine Primzahlen ergeben:
2 ist besser als 3
3 ist besser als 5
5 ist besser als 7
7 ist in der Praxis schon zu gross
Intervalle und Rhythmen
Das ist anders als bei Rhythmen, wo Bruchverhältnisse ebenfalls eine Rolle spielen. Weshalb das dort anders ist, und weshalb Rhythmen mit 7 oder 11 Schlägen gut klingen, lässt sich in der 3-Welten-Theorie plausibel erklären. Mehr dazu später.
Vom Pool zu den Tonleitern
Wir suchen nun nach weiteren Kriterien für attraktive Tonleitern. Der gefundene Pool ist ja noch keine Tonleiter, sondern nur unsere Ausgangslage, um daraus die Töne für verschiedene Tonleitern zusammen zu stellen. Dabei gelten weitere Kriterien.
Weitere Kriterien
4. Kriterium: Die Tonleitertöne sollen bevorzugt auch untereinander Resonanzen eingehen können
5. Kriterium: Die Tonleiter hat einen Grundton (eine sogenannte Tonalität), die in der Tonleiter eine ganz besondere Funktion hat.
6. Kriterium: Die Tonleitertöne dürfen nicht zu nahe beieinander sein, sonst können wir sie als Menschen (Laien) nicht mehr unterscheiden. Dies ist ein praktischer Constraint aus der mentalen Welt. In einer rein mathematischen Welt wären beliebige Differenzierungen denkbar, in der Realsituation ist das nicht der Fall.
Mehr zu den Kriterien für Tonleitern im Fortsetzungsbeitrag.
Dies ist ein Beitrag zum Thema 3-Welten-Theorie.