What is this about?
According to the theory of the three worlds, mathematics (ideal world) plays a part in physical processes (physical world). Without our subjective perception (mental world), however, we would not be able to notice any of this. I examine the way in which these very different worlds converge in reality with the example of musical scales. There are some riddles here, for instance why human cultures have created thousands of different musical scales, but every one of them uses the octave.
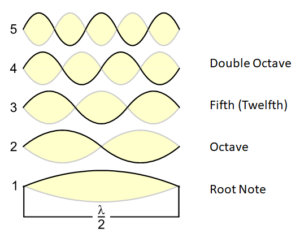
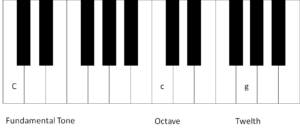
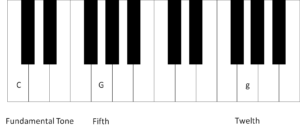
This constancy of the octave can easily be explained by resonance, which in the case of the octave is particularly striking because it corresponds to a mathematical ratio of 2:1. The higher tone of the octave vibrates with twice the frequency of the fundamental tone – an obvious example of how physics, mathematics and subjective perception come together.
In the preceding post I examined whether, with the help of mathematical considerations, we can find further intervals which occur in real musical scales. With only a few mathematical criteria, we found a first pool of intervals which have a high degree of affinity to resonance, i.e. the musical scale tone and the fundamental tone are in a frequency ratio which very easily produces a strong resonance.
Criteria for musical scale tones
Tone range
All musical scales known to me are situated within the range of an octave. This alone is amazing, and we have seen that all three worlds are involved in their creation.The crucial factor for the musical scale tones is their frequencies (f). What is decisive is not the absolute height of the frequency, but only its relative height in comparison with other tones. Below, the number 1 will denote the frequency of the fundamental tone and the number 2 the (doubled) frequency of the octave. All the musical scale tones must be situated between the fundamental tone and the octave; in mathematical terms, this means for the relative frequency f(ST)of the scale tone (ST) in relation to the fundamental tone:
1 ≤ f(ST) ≤ 2
2. Resonance
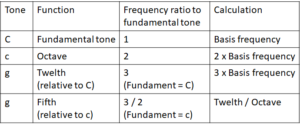
The physical precondition for resonance to occur is that two frequencies are in a “rational” ratio. In number theory, “rational” describes a number which can be written as a fraction of two integers. In other words: f2 = m/n f1 (m andn are integers, f1 and f2 are the two frequencies). We now hypothesise that a musical scale tone (ST) is preferably in a ratio (M/N) to the fundamental tone (FT) in which a resonance can develop. In mathematical terms, this is expressed as follows:
f(ST) = m/n f(FT)
This precondition is part of the physical and mathematical worlds and, independently of subjective and cultural perception, a generally valid physical precondition for resonance, also in the non-acoustic sphere.If calculating with interval fractions is new to you, I would like to recommend the annexes, in which the calculation processes and their backgrounds are described in detail.
3. Strong resonance
A resonance does not always occur equally quickly and equally strongly. Some intervals can therefore develop a resonance more quickly and more strongly than others. I hypothesise that a resonance is the stronger, the smaller m and n are, and I have examined, starting from number 1, what intervals we obtain with as small values as possible for m and n.Surprisingly, it turns out that all the small denominators up to 5 result in musical scale tones which we already know as the most important ones in our traditional European musical scales.The search also reveals that the absolute height of m and n is not the sole determining factor; rather, it comes down to the prime numbers which result from the integer factorisation of m and n. Here it turns out again that among the prime numbers, 5 is also the limit for the numerator. With this in mind 6, 8 and 9, which are not prime numbers, can be factorised (6=2×3, 8=2×2×2 und 9=3×3) and used for resonances. 7, however, which is a prime number, cannot be factorised and is therefore already too high for m and n in practice.
m and n should be as small as possible,
Or more precisely: In the integer factorisation of m and n, 5 should be the highest number.
Why integer factorisation? – The musical scale tone does not exist on its own, i.e. it should not only have a resonance in relation to the fundamental tone, but also in relation to the other musical scale tones. This results in compound resonances, mathematically speaking in fractions, in which numerator and denominator can often be reduced. This quickly turns an 8 into a 4, a 15 into a 3, and we again have very small m and n values. Examples will follow.
4. Further criteria
Resonance is not the only requirement for attractive musical scales. Musicians and listeners must also be able to distinguish between the tones. This is easier if there are not too many tones and if they are not too close together. These are not mathematical requirements, nor have they anything to do with resonance. The origin of this demand on a musical scale has something to do with our reception, i.e. with what we are able to perceive – that is, our mental world. With regard to this, our perception depend on the physics of our inner ear and on the physics of our brain. These criteria are thus a demand from the mental world, on the basis of the physical world. Evidently, all three worlds are involved in the creation of the many thousand different musical scales. The following are criteria that are not related to resonance:
4a) The number of the musical scale tones must not be too high.
4b) The musical scale tones must not be too close to each other.
Neither the number of tones nor their minimum distance from each other are the same in every culture. Besides resonance, there are further principles in music, namely that of interference and the higher/lower principle. If the tones are close to each other, music-related training provided by cultural experience may make precisely such tones interesting. However, this does not happen across the whole octave range of the musical scale, for if tones are very close to each other, the overall number of tones in the scale must still not become excessive. The distance between other tones must occasionally be wider again. A musical scale with quarter tones across the whole octave is conceivable but is unlikely to become prevalent in practice.Besides interferences and the higher/lower principle, there is a further principle, the variety principle. This has neither a mathematical nor a physical basis, but a mental one. If everything is the same, things become boring – and this also applies to the distances within a musical scale. This is why we do not experience the whole tone musical scale, which solely consists of identical intervals, as particularly exciting. Yet in combination with other scales with more variants, it is precisely that same whole tone musical scale which can provide an interesting contrast. Pieces of music that would only use whole tone musical scales would not be interesting for long. We thus have a further criterion which is not related to resonance:
4c) The distances in the musical scale should not all be identical.
4d) Fundamental tone principle:
The fundamental tone is the tone which holds the musical scale together. We will have a closer look at this in the section about ecclesiastical modes. As a consequence of the fundamental tone principle, we will always relate the musical scale tones to the fundamental tone.
We compare all the musical scale tones through the fundamental tone.
With the help of these conditions, we will examine our pool of intervals from the preceding post and filter out some first musical scales. Not surprisingly, they are musical scales which do not only have a simple mathematical structure, but also exist worldwide. They are certain pentatonic scales which are not only in use in their pure forms around the globe, but are also contained as a basic structure in more complex musical scales, such as our standard major scale. Firstly, we will have a look at the most resonant musical scales.
Here you can find an overview of the texts about the theory of the three worlds.