The equal temperament has prevailed in our occidental music culture – despite the obvious shortcoming that its intervals are not pure any longer. This was only possible because some substantial advantages offset the flaw of impurity:

1.  One single tuning serves all keys: the fundamental tone is freely selectable.

In pure intonation, instruments basically have to be retuned for each key and each fundamental tone. With a harpsichord, this concerns a few strings, but with an organ, this is really a great undertaking in view of the vast number of registers and pipes. The further the keys are apart from each other – i.e. the more crosses and Bs they have – the worse the detuning is. The equal temperament changes all this. Although it is never quite pure, it is never so detuned as it would be in a distant key, either. With the equal temperament, instruments can be used to play in a different key immediately without retuning. Organs, string, wind and any other instruments can now play together in all keys.

2. Free modulation

This advantage is particularly obvious and effective. In the same piece of music, we are now able to change from one key into any other (modulate) – without any break and retuning. With pure intonation, this is only possible in a limited way and for closely related keys. The equal temperament, however, removes all the limits to modulation.

3. “Bonus keys”

The seven tones of the major key do not merely serve to play major scales. On the white keys of the piano, you can play all the seven ecclesiastical modes, depending on which of the seven tones you choose as the fundamental tone:

C: Ionian = major
D: Dorian
E: Phrygian
F: Lydian
G: Mixolydian
A: Aeolian
B: Locrian

The same applies to the pentatonic scales. If you only press the black keys on a piano, for example, you will automatically play pentatonically (penta = five → five black keys). Depending on which tone you choose as the fundamental tone, you will play a different pentatonic scale, for instance the major pentatonic scale (with F sharp as the fundamental tone) or the minor pentatonic scale (with E flat as the fundamental tone).

This principle of generating new scales with the tones of an existing scale also applies to the ‘melodic minor’ scale in jazz. As the major scale, the melodic minor scale is a selection of seven tones, but in intervals that cannot be played with the white keys of the piano alone. With these seven tones of the melodic minor scale, we are again able to construct seven different musical scales which differ greatly in terms of character, merely depending on which tones we choose as the fundamental tone.

4. Polytonality

This stylistic device emerged in the 20th century with Stravinsky and other composers, and it is also used in modern jazz. To achieve this, several keys are mixed; in practice, it is usually two (= bitonality). This appears to be slightly risky at first sight, but if we take into account the resonances (!) correspondingly, it actually sounds quite catchy.

Conclusion from the perspective of the theory of the three worlds

The mathematical purity (Platonic world) of the interval resonances is violated by the temperament, but in such a minimal way that the resulting vibration phenomena (physical world) are produced all the same and the listening experience (mental world) is hardly diminished at all.

On the other hand, free modulation extends the number of possible combinations of the still only twelve tones immensely. This mathematical extension (Platonic world) is audible and exciting (mental world). Through minimal impurity, music gains in variants and richness.

This is a post about the theory of the three worlds.

Starting point: two gaps

In the previous post, we saw that in the sequence of the ten scales tones found so far, there are two gaps. Can we find resonant tones there, too? We already know the following:

• We already know the ten most resonant intervals in the octave.
• These ten intervals serve to constitute the five standard pentatonic scales and our major and minor scales. There, the gaps are not obtrusive; they are only conspicuous in the distribution of all the ten potential scale tones.
• Intervals do not occur on their own, either in a chord or in a melody. Thus if we have a resonant interval, we add another one to it and calculate the resulting sum interval. Or we look at the distance between two intervals and calculate the distance between both intervals, i.e. we subtract one from the other.
• Owing to the exponential progression of the frequencies, and contrary to our intuitive expectation, when we calculate the frequency of the two intervals added together, we do not have to build the sum of the two interval fractions, but have to multiply them, and with regard to the distance between the two intervals, we must not subtract one interval from the other, but divide one by the other.

Since we have already found all the resonant intervals within the octave, we cannot expect any more highly resonant intervals for the two gaps. Yet although, if we are successful, the intervals are not all that resonant any longer in terms of their resonance with the fundamental tone, they may still have direct and thus very resonant relations to other scale tones. In musical configurations, this also makes them interesting in terms of resonance, depending on the situation.

Here are my attempts to fill in tones for the gaps. To illustrate this, I will first show the distribution of the ten most resonant intervals from the previous post:

Fig. 1: Distribution of the ten most resonant scale tones in an octave (logarithmic representation)

The minor seconds

Regarding the first gap, we cannot find a tone with good resonance with the fundamental tone. Because the two tones of the interval must be close together, the fraction of their frequencies must be close to 1 and therefore its numerator and denominator cannot be small numbers – as would be preferred for a good resonance. We therefore check as candidates fractions that are still created by relatively small numerators and denominators:

Octave – major seventh = 2 : 15/8 = 16/15 = 1.067
Fourth – major third = 4/3 : 5/4 = 16/15 = 1.067
Minor sixth – fifth = 8/5 : 3/2 = 16/15 = 1.067
Minor third – major second = 6/5 : 9/8 = 48/45 = 16/15 = 1.067
Major third – minor third = 5/4 : 6/5 = 25/24 = 1.042
Major seventh – minor seventh = 15/8 : 9/5 = 75/72 = 25/24 = 1.042
Major sixth – minor sixth = 5/3 : 8/5 = 25/24 = 1.042
Minor seventh – major sixth = 9/5 : 5/3 = 27/25 = 1.08

In this way, we can find several intervals which satisfy the requirements and fit into the first gap:

• 16/15 = 1.042
  – major third – minor third
  – major sixth – minor sixth
  – major seventh – minor seventh
• 25/24 = 1.067
  – minor third – major second
  – minor sixth – fifth
  – fourth – major third
  – octave – major seventh
• 27/25 = 1.08
  – minor seventh – major sixth

These three intervals all sound rather twangy. We call them minor seconds. In the pure temperament, there are at least three of them.

The tritones

The second gap is right in the middle of the musical scale. We are now going to try to fill this gap with a combination of two known resonant intervals:

Major seventh – fourth = 15/8 : 4/3 = 45/32 = 1.406
Minor seventh – major third = 9/5 : 5/4 = 36/25 = 1.44
Major sixth – minor third = 5/3 : 6/5 = 25/18 = 1.389
Octave + minor third – major sixth = 2 x 6/5 : 5/3 = 12/5 : 5/3 = 36/25 = 1.44

Once more, this results in three intervals that are close together:

• 25/18 = 1.389
• 45/32 = 1.406
• 36/25 = 1.440

Insertion of the minor seconds and the tritones into the sequence of the scale tones

Our calculations so far have concerned frequency ratios. As explained in the previous post, we have to convert them logarithmically to ensure that their distances correspond to what we perceive in our mental world. In a logarithmic representation (on basis 2), we arrive at the following distribution:

Fig. 2: The three minor seconds (“semitones”) and three tritons fill the gaps of Fig. 1

Although we can see that the proposals fill their respective gaps well, we have three proposals for each gap! Which of them is the best? We could argue in favour of that with the smallest figures in the numerator and denominator, or in favour of that with the greatest frequencies among the variants, or in favour of that with the closest relation to a musical scale we already know. However, it is for a good reason that we defer this issue until we deal with the well-tempered scales.

This is a post about the theory of the three worlds.

The ten most resonant tones within the octave

In this series of texts, we examine musical scales from the perspective of the three worlds. All three worlds are involved, as we saw, for example, when we answered the question as to why the musical scales of all musical cultures always cover precisely one octave. This cannot be explained in purely mathematical or physical terms. It is only through the involvement of the third world, namely our mental world, that the significance of the octave becomes evident.

The selection of the tones used in a musical scale is determined by all three worlds through the phenomenon of resonance, as we saw in previous posts. Let us now have a look at how the ten most resonant tones are distributed within the span of the scale octave. We will see that there are gaps in this distribution, and then think about what conclusions we can draw from this.

Here are these ten tones once again. (The table lists eleven tones, but the fundamental tone and the octave count as one tone, since the octave is both the highest tone in the present octave and simultaneously the fundamental tone of the next higher octave, in which the musical scale repeats itself.)

Table 1: The ten most resonant tones in an octave 

The middle column of Table 1 lists the fractions which indicate the ratio between the scale tone and the fundamental tone; with the fifth, for instance, the frequency is 3/2 times the fundamental frequency. On the far right, I have expressed these fractions as decimal numbers to make comparisons easier. Of course, the numbers range from 1 (fundamental tone) to 2 (octave).

 The distribution of the ten tones

To see how the ten tones are distributed within the octave, we take the frequencies of the tones and compare them with the frequency of the fundamental tone. These frequency ratios are in the right-hand column of Table 1. I have transposed these numbers into Figure 1, and you can see how the frequency ratios are arranged linearly.

This is what the arrangement of the intervals of Table 1 looks like:

Fig. 1: Frequency ratios of the potential scale tone (Table 1) in linear representation. Here, the intervals are regarded as starting from C, i. e. C = fundamental tone.

In Fig. 1, we are immediately struck by how irregular the distribution is. It displays four major gaps, namely between C and D, F and G, A and B, and H and C. Subjectively, the distribution does not appear to be , either; for example, the distance between the fundamental tone and the fourth (C-F) is much shorter than that between the fifth and the octave (G-C). However, we perceive both intervals as the same, namely as two fourths, for the distance between G and C is also a fourth, just like that between C and F. Nonetheless, the distance between G and C in Figure 1 is much longer than that between C and F. Why does the perceived distance not correspond to the real frequency ratio? – The answer is again in the exponential progression of the frequencies (physical world), which does not correspond to our linear perception (mental world). We therefore have to notate the frequencies logarithmically, thus arriving at a representation which corresponds to our subjective perception:

Fig. 2: The frequency ratios of Fig. 1 in a logarithmic representation.

We can see that in Fig. 2, the distances correspond to our subjective perception as being truer to scale. Thus, in contrast to Fig. 1, the distance between C and F is the same as between G and C, which we perceive as correct, namely as a fourth each time. The other distances in Fig. 2 also correspond to our perception.

The distribution still looks irregular, though, and there still are gaps. However, these have also shifted now. The gap between C and D has become bigger, whereas that between H and C has become smaller. What is really conspicuous are the two gaps C-D and F-G. Will we be able to do something here? Will we once more be able to resort to our reflections on resonance in order to fill the gaps? I will explain how this works in the next post.

This is a post about the theory of the three worlds.

The major scale

The major scale (Ionian mode) is the most widespread musical scale both in Europe and globally. It is a heptatonic scale, i.e. a musical scale with seven tones. It is characterised by very special resonance ratios, which serve well to explain its worldwide appreciation.

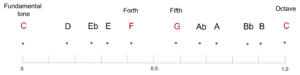
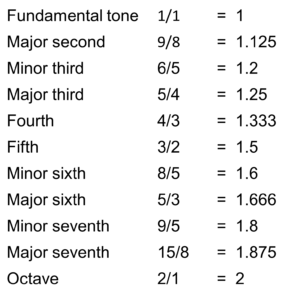
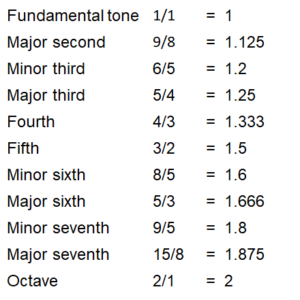
Below, I have listed the tones of the major scale of C, ascending from the bottom to the top, together with the intervals between each tone and the fundamental tone. Of course, it is these intervals that constitute the musical scale. We could also start the musical scale with any other tone and only speak of the intervals (second, third, etc.) since we only need the distances between the tones to describe a musical scale. However, I am using the tone of the C major scale, simply because it is clearer and also enables you to reproduce it more easily on a piano or other instrument.

The interval designates the ratio of the frequency of a scale tone to the frequency of the fundamental tone. This interval always lies between 1 (fundamental tone) and 2 (octave) in every musical scale. We express it in the form of a fraction.

C      2
B      15/8
A      5/3
G      3/2
F      4/3
E      5/4
D      9/8
C      1

Table 1: The C major scale

The fractions enable us to recognise what is typical of the major scale. It can be shown very well that what we hear subjectively (mental world) is perfectly in parallel with what we are able to represent mathematically in simple fractions (Platonic world). It turns out again that the three worlds (according to Penrose) interact perfectly in the field of music.

All the tones resonate with the fundamental tone

In a previous post, I established resonance criteria for scale tones. These criteria yield ten tones which strongly resonate with the fundamental tone. Like the standard pentatonic scales, the major heptatonic scale consists of a selection of these ten most resonant tones. Thus we may assume that the major scale is generally strongly resonant in itself. Yet not every tone is equally resonant with the fundamental tone. And among themselves, in particular, tones resonate very differently. This is where the story becomes interesting. To begin with, we’ll have a look at the difference between the major heptatonic scale and the major pentatonic scale.

The major heptatonic scale as an extension of the major pentatonic scale

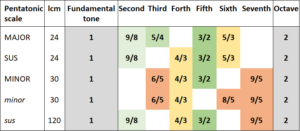
The standard pentatonic scales are the most strongly resonant musical scales in general, and the most resonant of them is the major pentatonic scale. The major heptatonic scale can be regarded as an extension of the major pentatonic scale. Both musical scales are subsets of the ten most resonant tones.

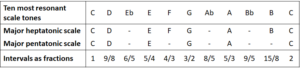
Table 2: Comparison between the major pentatonic and the major heptatonic scales

The tones which are added to the heptatonic scale in comparison with the pentatonic scale explain the difference. Whereas the pentatonic scale is resonant throughout and all tones can be mixed at random without any tensions occurring, this is no longer the case with the heptatonic scale. The two additional tones, F and H, introduce the necessary tension for the matter to become interesting.

The first thing that strikes us is the fact that with H, that tone is added which among the ten most resonant tones has the highest digits in the numerator and the denominator. Among the ten most resonant tones, it is therefore the tone that resonates most poorly with the fundamental tone, the tone that creates most tension. This concerns its relation to the fundamental tone.

However, the intervals between different scale tones apart from the fundamental tone play a role in musical scales, too. We calculate this by dividing the frequency ratio of the upper tone by that of the lower tone (for the reasons for dividing, cf. Appendix). The two new additional tones in the heptatonic scale, i.e. F and B, generate a tension both mathematically and audibly such as has not occurred in the pentatonic scales so far. If, for instance, we sound F together with E, then this results in a frequency ratio of 4/3 : 5/4 = 16/15, a fraction which indicates a resonance that is difficult to achieve. H and the upper C sounded together have a similar result; here, the ratio is 2/1 : 15/8 = 16/8 : 15/8  = 16/15. Thus the interval between H and C is as full of tension as that between E and F. The interval between F and H is even more critical; here, the fraction is 15/8 : 4/3 = 45/32. These are two high numbers indeed, compared to what we have seen before, and they offer no possibility of reducing.

Tension and easing

Poor resonance means tension since both tones do not easily go together. We apprehend this subjectively (mental world), as you can easily find out by striking an E and an F at the same time on the piano and comparing the sound with the simultaneous sounding of, say, E and G. E and F produce more friction. Physically, the mathematics of the frequency ratios express a lesser or higher degree of readiness to enter into a resonant relationship, and we can hear this.

Musically, however, tension is not without interest. The major pentatonic scale without F and H may strike us as quiet and harmonious, but also as a bit dull. Conversely, the major heptatonic scale contains little peppercorns which introduce an exciting pungency, similarly to the hotness of chilli peppers in a dish. Yet whereas you can still feel this hotness as a long aftertaste, this pungency in music can be switched on and off with precision by simply replacing the tone that creates tension with a quiet one that resonates without any problem. This interplay of tension and easing is extensively used in music.

The major heptatonic scale as a subset of the ten most resonant tones

As illustrated in Table 2, the major scale is a selection of seven tones from the list of the ten most resonant tones. This selection packs a punch. I will shortly deal with the mathematical details which result from it. You will probably not be surprised that these mathematical details are again in parallel with our listening experience. Let’s first look at which of the ten tones are missing in the major scale: they are Eb, Ab and Bb. As always, we look at the fractions of these three intervals: 6/5, 8/5 and 9/5. We quickly notice that all these fractions have the denominator 5. Conversely, none of the tones in the major heptatonic scale do have the denominator 5.

Reducing the denominator

This fact of the missing denominator 5 facilitates the resonances within the major heptatonic scale. If two tones have the same denominator, this is cancelled out when we sound the two tones simultaneously. If, conversely, there are different denominators, resonance will be made more difficult. Different denominators, however, can be reduced too, if they can be divided by each other.

For this purpose, we conduct an integer factorisation. In the major scale, for example, the major seventh and the major third resonate perfectly with each other: in order to calculate the resonance mathematically, we divide the major seventh by the major third, which results in 15/8 : 5/4 = 3/2. These 3/2 luckily indicate a perfectly resonant interval, namely the fifth.

The cancelling in this case is possible because in integer factorisation, both the denominator 8 and the denominator 4 contain the prime number 2 twice (8=2×2×2 und 4=2×2). Thus the factor 2 can be cancelled out (even twice, since both denominators contain it twice). This cancelling (reducing) can be done whenever two numerators contain the same factors.

For this reason, it is “clever” of the major scale to omit precisely all the tones with the denominator 5. In this way, the 5 never intrudes, and reductions are more easily possible. And reduced fractions with regard to the frequency ratios mean better resonance both physically and mentally.

The resonance of the totality of all scale tones together

We can roughly estimate the reduction behaviour of the totality of all the tones in a musical scale by calculating the lcm (least common multiple) of all the denominators, as we already did with the pentatonic scales. The tones of the major heptatonic scales have an almost unbeatable lcm of 24; it is even the same as that of the major pentatonic scale with two fewer tones.

This low lcm is of course the result of the fact that there aren’t any tones with the denominator 5 in the scale; otherwise we would have to multiply the lcm by 5, which would result in 120.

The lcm is useful but does not say everything

However, the lcm doesn’t show the whole resonance behaviour of the musical scale. It is only a measure for the resonance of all the scale tones with the fundamental tone, but does not say anything about how the scale tones resonate with each other.  For the above-mentioned interval of the tones F and B, for instance, we obtain a frequency ratio of 45/32, which means that even if the tones resonate well with the fundamental tone, they can be full of tension among themselves.

This is not a weak point, though; rather, it makes the musical scale interesting. In this respect, the major heptatonic scale is clearly more interesting than the major pentatonic scale although both of them have the same lcm.

Nonetheless, the lcm is a valuable yardstick against which the basic resonance potential in the musical scale can be roughly measured, since with a high lcm, i.e. when the denominators cannot be reduced, the dissonances are sharper in any case.

Triads in the major scale

We now turn our resonance considerations to three tones that are sounded simultaneously. Let us analyse the triad of C, E and G. The frequencies (cf. Table 1) are: 1 – 5/4 – 3/2. To calculate the ratio of all three tones to each other, we must place all three of them on the same denominator. It is precisely for this that we need the lcm again, which in this case is 4. Thus 1 – 5/4 – 4/2 results in a ratio of 4/4 – 5/4 – 6/4. The common denominator can be cancelled out, and the ratio of the frequencies of C-E-G is 4 – 5 – 6.

This is absolutely the most resonant ratio which is possible when three different tones are sounded together. The C-E-G triad is the major triad with which everyone is familiar. On the piano, it is slightly distorted due to temperament, but even so you can easily try out for yourself how catchy and attractive this triad is. No wonder it plays such a dominant role in pop and folk music.

Three major triads in the major heptatonic scale

However, the major heptatonic scale does not contain the major triad only once, but three times. Look at the tones F – A – C, in fractions 4/3 – 5/3 – 2, or all the tones placed on the common denominator 3: 4/3 – 5/3 – 6/3, i.e. again 4 – 5 – 6. This demonstrates once more the benefit which the common denominator (here: 3) represents for the resonances. Thus the major heptatonic scale did well to include the tone of F, which allows for a second major triad.

But H is also well chosen, for it enables a third major triad in the major heptatonic scale. This time, we start with G and add H. As a third note, we take D, an octave higher than usual, i.e. just above the upper C. For this purpose, we have to multiply the 9/8 of D by 2, which results in 9/4 (cf. calculation rules).  This fraction is higher than 2, i.e. is already above the octave. Let us now look at the tones G – H – D; the frequencies are 3/2 – 15/8 – 9/4. With the lcm=8, we obtain 12/8 – 15/8 – 18/8. We can now reduce the numerators and denominators, which again results in 4 – 5 – 6, i.e. the same ratio as above, the same perfectly resonant major triad as those with the roots C or F.

Thus the major heptatonic scale contains the major triad no fewer than three times, for three tones of the heptatonic scale can be combined in this most resonant manner three times. What is also remarkable, however, is the fact that the three triads do not mix very well with each other. This is easily heard; again, the mathematics perfectly corresponds to our subjective mental experience (sorry, I have to mention this thing with the three worlds again and again; I myself am surprised how well they converge in musical scales).

Of course, the major scale was not “invented”, and certainly not by a mathematician. Rather, this musical scale was found by people who themselves actively made music and thus became aware of the particularly interesting resonance relationships which result from the combination of tones.

As we just have seen, there are three independent collections of tones inside the major scale which resonate well within themselves but harmonise less well with the other selections. This results in three different colours or harmonies inside the major scale which can be used separately and whose sequence can be planned in a piece of music and thus tells us a story. The three colours are defined by the root of each triad, namely by the fundamental tone of the musical scale (C), its fourth (F) and its fifth (G). The three tones are called tonic (fundamental tone), subdominant (fourth) and dominant (fifth). The possibility of playing with such colour far exceeds the possibilities of the major pentatonic scale and was studied and perfected in Europe throughout the course of the centuries.

Minor triads

These triads, too, have a special resonance ratio, namely 10 – 12 – 15. The numbers are slightly higher than in the major triad, which makes the minor triad slightly less resonant. For three different tones, however, the ratio is still extremely simple and thus resonant, and minor triads are certainly not dissonances.

In the minor triad, the minor third is the first tone with a frequency ratio with the denominator 5, whereas the major scale does not have this and prefers denominators based on the prime number 2. This produces a distinctly different colour. With the denominator 5, we have already reached the highest “permitted” prime number, much higher than 2 and its easily divisible multiples found in the major scale. The minor scale therefore sounds softer, more special and not as as the major scale.

The minor triads cannot only be found in the minor heptatonic scale but also in the major heptatonic scale, simply based on less prominent scale tones, specifically on D, E and A. In principle, minor colours can also be produced in the major scale, even though only on less prominent tones.

Conclusion

All in all, the seven tones of the major scale constitute an almost inexhaustible source of combinations. The major scale combines a maximum degree of resonance with the possibility of generating tension and different colours. All this can be easily reconstructed by means of simple mathematical fractions – in complete harmony with what we hear subjectively.

To continue, we will have a look at the Pythagorean comma. This is particularly interesting because it shows how the mathematical world reaches its limits in the physical world. This fact has resulted in an evenly tempered intonation, an “impure” intonation. So have a look at how the Pythagorean comma emerges.

This is a post about the theory of the three worlds.

As we have seen in the previous post, the tones C – D – E – G – A – C constitute the standard major pentatonic scale.

All in all, another four pentatonic scales can be created with the simple criteria for resonant pentatonic scales. These five pentatonic scales are the five musical scales which according to our mathematical criteria allow for resonances among all their tones.

We will see later on that we are able to create all the musical scales traditionally used in Europe with our pool of the nine most resonant tones. In the heptatonic scales, however, for instance in our diatonic major scale, certain tones resonate poorly with each other, which is actually more interesting in musical terms, since this creates a natural structure within the scale tones.

Conversely, pentatonic scales do not have any “wrong” tones however we mix them. It appears as if there would be no resistance, no matter which tones we sound together.

The five pentatonic scales are:
(on the basis of C)

C –  D  –  E  –  G  –  A  –  C

C –  D  –  F –  G  –  A  –   C

C – Eb – F –  G   – Bb  – C

C – Eb – F –  Ab – Bb  – C

C – D  –  F –  G   – Bb  – C

The same tones in fractions:
(fundamental tone = 1)

1 – 9/8 – 5/4 – 3/2 – 5/3 – 2

1 – 9/8 – 4/3 – 3/2 – 5/3 – 2

1 – 6/5 – 4/3 – 3/2 – 9/5 – 2

1 – 6/5 – 4/3 – 8/5 – 9/5 – 2

1 – 9/8 – 4/3 – 3/2 – 9/5 – 2

For the purpose of the calculation, I assume that all the tones are sounded simultaneously and within an octave with the fundamental tone as the lowest tone. Thus I calculate the intervals between each tone and the fundamental tone. Then I look at the denominators of all the intervals and look for the least common multiple (lcm) of these denominators. This shows how easily resonances can occur between all the tones:

How do you read Table 1?

I have placed the same intervals of the different pentatonic scales in the same column. This results in holes in the table. Thus the major pentatonic scale does not have a fourth and a seventh. Furthermore, I have given tones with the same denominator in the fraction the same colour.

What do the colours show? – As we know, identical denominators mean that the two tones are particularly resonant because in the calculation of their frequency ratio, the two denominators “reduce themselves away” when the tones sound together. This leads to particularly simple, i.e. particularly resonant ratios between tones with the same denominator. For seconds, major thirds and fifths, I have chosen three different shades of green. The denominators are not identical but are always based on the prime number 2, which means that a reduction by two is always possible. Therefore the different greens always mix very well.

In mathematical terms, the major second has the highest denominator of all intervals in the pool – 8 – but this is not a problem. 8 is not a prime number, but 2³, just as the denominator of the major third, 4, equals 2². If we sound the fifth together with the major second, the ratio of the two tones is 3/2 : 9/8 = 3×8 / 2×9 = 4/3, i.e. a fourth. The fourth is the third most resonant interval that is possible within an octave; a major second and a fifth are therefore perfectly resonant. Reduction proves effective.

Furthermore, the colours in Table 1 also show the different forms of the third and the sixth. Thus the 5/4 third is the major third and the 6/5 third is the minor third.

Musical scales are about the interval between scale tones and the fundamental tone, but also about the ratio of scales tones among each other. The lcm is the indicator of how close the resonances are in this respect. The lower the lcm, the more resonant the musical scale as a whole. However, critical tones can also be omitted or inserted into a melody as a special accent, but this is hardly possible in the standard pentatonic scales with their low lcms.

How do the five pentatonic scales differ from each other?

Major and minor scales

In functional harmony, a genuine and trailblazing European invention, the third plays an important part. Whether major or minor is a question that is always being asked. However, we are not going to deal with functional harmony (yet), but we can nevertheless look at our five pentatonic scales from the perspective of the third. We then see that we have a major pentatonic scale (with a major third) and two minor pentatonic scales (with a minor third).

The two minor pentatonic scales differ from each other in that one of them does not have a fifth. Although the lcm is the same and low in both cases, the lack of a fifth is a great handicap musically (and with regard to resonance), which is why the minor pentatonic scale without the fifth is hardly ever used. Our customary minor pentatonic scale is the one with the fifth.

When you look at Table 1, you can see the difference at once by the colours: the minor pentatonic scales has tones that are reddish in colour (denominator 5) whereas the major pentatonic scale does not. In each case, the third attracts further intervals with the same denominator. The reason for this is to be found in resonance again: identical denominators guarantee strong resonance.

Sus pentatonic scales

The term “sus” derives from “suspended fourth”. Where does the expression come from? – In classical European music, i.e. in functional harmony, the third is the crucial factor. A chord which does not have a third but has a fourth instead, is suspended, i.e. it must first be resolved; the fourth is regarded as a suspension and must be resolved into the major third. In other styles such as jazz or modern pop music, the sus chord is a chord like any other, a colour like minor and major. There are also sus musical scales without thirds, whether minor nor major, both in world music and in jazz. After the octave and the fifth, the fourth (4/3) is the most resonant interval.

Again, there are two forms of sus pentatonic scales. The high lcm of 120 of one pentatonic scale results from the fact that it has both a major second (denominator = 9) and a minor seventh (denominator = 5), which means that reduction is not possible (as you can work out for yourself if you calculate the lcm yourself). The sus pentatonic scale with the sixth has another problem: the fourth and the sixth combined with the upper fundamental tone constitute a major chord (4/3 – 5/3 – 6/3 →4-5-6). This major chord on the fourth is extremely resonant and thus becomes so dominant that the musical scale is easily misinterpreted as a major pentatonic scale.

Which pentatonic scales are commonly used?

As a consequence of the above-mentioned weaknesses of the one minor pentatonic scale and the two sus pentatonic scales, only the major pentatonic scale and the minor pentatonic scale with the fifth are commonly used. However, these two pentatonic scales are ubiquitous and very easy to sing. They can also be combined with other musical scales/chords in a melodious way, which is of particular musical interest. On their own, they sound somewhat commonplace, but show their whole strength in combinations. They are perfect building blocks for musicians.

To continue, we’ll have a look at the major musical scale. How resonant is it?

You can find an overview of the texts about the theory of the three worlds here.

Sine waves play a crucial part for our considerations of resonance. On this page, I would like to explain the terms that I use in this respect.

Wave

A wave is a motion in time which oscillates around a baseline.

A wave can have different shapes. For our considerations of resonance, we use pure sine waves; such a wave is shown in the graph above.

Amplitude

The amplitude is the deviation of a wave from the baseline. It does not play any primary role in our considerations.

Period

A period lasts as long as the wave takes to arrive in the same position to repeat itself again in precisely the same way. Depending on the shape of the wave, it crosses the baseline two or more times; in the case of the sine wave, it crosses it twice in opposite directions.

Wavelength

The wavelength is the length of a period.

Frequency

Frequency denotes the number periods per unit of time. It is the crucial value for our considerations of resonance, for whereas amplitudes and wavelengths change depending on the carrier medium of the wave, the frequency remains the same if the wave is transferred from one medium to another.

“Belly”

In each period, the sine wave has one belly in the positive direction and one belly in the negative direction. When we count the number of bellies per unit of time, we thus measure the frequency, i.e. counting bellies measures the frequency. This slangy expression has the advantage of being graphically illustrative. At the same time, the term “belly” emphasises indivisibility (mathematically: whole numbers!), whereas the frequency can be expressed in any real number.

With respect to resonance ratios, we always compare whole numbers, i.e. the number of completed bellies. Whether we only count the positive bellies or both the positive and the negative ones is irrelevant, since in a frequency comparison, only the relations of the frequencies matter.

Natural frequency

Certain physical media (strings, air columns in pipes, etc.) have the property of oscillating (vibrating) in a very specific frequency, their natural frequency.

Fundamental tone and overtones

Besides the natural frequency as the fundamental frequency (fundamental tone), the medium can also oscillate with a multiple integer of the fundamental frequency. Multiple integer means that the crucial factor is the number of whole periods (bellies).

On this page, I will explain some rules which are applicable when we calculate with intervals and their frequencies.

Intervals are fractions

An interval ranges from a lower tone to a higher one. The fraction of the interval is calculated by dividing the frequency of the higher tone by the frequency of the lower tone, for instance

E  =  330 Hz
A  =  440 Hz

440/330 = 4/3. This is a fourth. The interval of the fourth is always 4/3: in the fourth, the higher tone is precisely 4/3 times as fast as the lower tone.

What counts here are only the relative values, not the absolute ones. Whether I start the fourth with the E (E-A) or with the C (C-F) is immaterial; the relative frequency ratio is always 4/3. In other words, intervals are always relative.

The exponential progression of the frequencies

When we compare the intervals with each other, there is a crucial feature: the progression of the frequencies is exponential.

Fig. 1: The progression of the frequencies is exponential

In Fig. 1, you can see the frequencies of various A tones, from the great A (capital letter) to the treble a” (small letter with two inverted commas). On the piano keyboard, it looks as if the distances between all four As are the same, but if we look at the frequencies, the distances become increasingly bigger. In other words: the frequencies increase faster than the intervals. In mathematical terms, the intervals progress in a linear fashion whereas the frequencies progress exponentially. This has some consequences for calculations with intervals.

Adding intervals

When we add two intervals, then this is a multiplication with regard to frequencies. Thus the tone of the (great) A has the frequency of 110 Hz. When we move up an octave, then the (small) a has twice that frequency, namely 220 Hz. The distance between 110 Hz and 220 Hz is 110 Hz. Yet this 110 Hz is only an octave if we start with the capital A. If we move up another octave from the small a, we must not add the 110 Hz of the lower octave (which would result in 330 Hz), but have to add 220 Hz, thus getting from 220 Hz to 440 Hz.

Our spontaneous idea that an octave corresponds to a value in Hz is incorrect. An octave means that the lower frequency is multiplied by 2 (with 2 because the octave always doubles). The addition of the intervals becomes a multiplication. At first sight, this change in arithmetic operations may be confusing, but once we’re aware of it, the matter is not so difficult. We must therefore remember:

the addition (of intervals) becomes a multiplication (of frequencies)

Subtracting intervals

Unsurprisingly, subtractions work in perfect analogy. Subtractions become divisions.

Example

We are looking for the distance between a major third and the fifth above it. Our knowledge of music tells us that the distance between the two intervals is a minor third. Can we also calculate this?

In this comparison, we subtract the major third from the fifth. But instead of subtracting, we divide:

Fifth                 =  3/2
Major third  =  5/4

Fifth – major third → 3/2 : 5/4 = 3×4 / 2×5 = 12/10 = 6/5

As we know, 6/5 is the minor third. This method always works, for any interval:

To check, we can add the two thirds again and the result – of course with a multiplication – is:

5/4 x 6/5 = 30 / 20 = 3/2

The major and minor thirds again result in the fifth (3/2) in this way.

The advantage: we are able to reduce!

The shift from addition and subtraction to multiplication and division has the advantage that with fractions we are able to reduce, as shown in the above examples, we are able to reduce.

This has a direct impact on the resonances: whenever we are able to reduce, the numbers in the fractions become smaller – and small numerators and denominators in the fractions are an advantage for resonance. This also explains why we prefer not to have any prime numbers higher than 5 in the intervals. Non-prime numbers such as 6, 8, 9, 10, etc. can be reduced, which is why we can find a major second (9/8) in common musical scales, but no intervals with the fractions of 7/4 or 8/7.

Relating scale tones to each other

When we compare two tones within a musical scale in order to decide whether they resonate with each other, we always relate them to their shared fundamental tone. This is essentially connected with the character of musical scales (and chords). All tones of a musical scale are based on this one fundamental tone (tonality).

Since the intervals are always relative, the crucial factor is not the absolute frequency of a tone, but its relation to the fundamental tone. When we set the

fundamental tone = 1,

all scale tones are described as relations of their frequency to the frequency of the fundamental tone.

Distance between two scale tones

What, for example, is the relationship between the fourth and the fifth? The fourth is 4/3 above the fundamental tone, and the fifth is 3/2. If we want to compare these two tones, we can calculate the distance between them. The distance is a subtraction, and with frequencies, a subtraction is a division. We divide the higher tone by the lower one, and the result is: 3/2 : 4/3 = 9/8.

9/8 is a major second; the distance between the fourth and the fifth is a major second.

Resonance between the fundamental tone and two scale tones

Whenever we look at two scale tones, they always have the fundamental tone in their foundation. The fundamental tone determines the tonality, and the tonality places the musical scale on an absolute basis.

But how do the three tones mix – fundamental tone, fourth and fifth?

For resonance to be generated, all three tones must stand on a shared base, or mathematically speaking, they require something like a shared counting time for all three frequencies, i.e. for the fundamental tone (1), the fourth (4/3) and the fifth (3/2).

For this purpose, we look for the smallest denominator which tallies for all three figures. In the example, this is the denominator 6:

Fundamental tone    1     =   6/6
Fourth                            4/3  =   8/6
Fifth                                 3/2  =   9/6

This common denominator is always the lcm, the least common multiple of all the individual denominators involved.

A further example

Fundamental tone    1    =  15/15
Minor third                 6/5  =  18/15
Major sixth                 5/3  =  25/15

The lcm of 1, 5 and 3 is 15.

What does this common denominator of several tones mean?

I propose the hypothesis that resonance occurs more easily, the smaller this common denominator is. For our consideration of resonance, the following applies on the basis of this hypothesis:

Tones which have a low common denominator mix easily.

The higher the common denominator, the smaller the internal resonance of the tones. 

The consequences of these conclusions are dealt with in the text about specific musical scales and chords.

This is where you will find an overview of the texts about the theory of the three worlds.

Starting position

Do the criteria which we have postulated so far already enable us to create musical scales which are so attractive that they occur in reality? After all, the criteria look rather artificial and theoretical at first sight – can they nonetheless serve to explain musical scales that have grown naturally?

Indeed they can. The mathematical criteria for resonance have obviously had an impact on the human ear and have for millennia prompted people again and again to invent music which is fundamentally structured by precisely those musical scales that we are able to derive mathematically with the help of our criteria.

Pool of resonant tones

With our resonance criteria alone, we established a first pool which contains those tones of which we expect the strongest resonance with the fundamental tone. I list these nine potential scale tones again below:

Of course this is merely a pool of many tones, and not a meaningful musical scale. The problem is that all these tones can easily and quickly resonate with the fundamental tone – but do they also resonate among each other?

Two scale tones and the fundamental tone

Thus this is not solely about the resonance of a tone with the fundamental tone, but additionally about its resonance with other tones. This has a mathematical basis: we have a look at the lcm (least common multiple) of the denominators involved. How this works, and why this is the case, is explained on the page of calculation principles for resonances.

The lcm (least common multiple) of the denominators

The resonance criteria indicate a good resonance if the lcm of the denominators involved is as small as possible. The fundamental tone has the denominator 1 and therefore fits every lcm; therefore it will fit every combination well. But how do the scale tones fit each other?

Example 1

Fourth and fifth: The denominators are 3 and 2; the lcm is 6, i.e. low. The numerators are also low. By way of a further indication of resonance, we can calculate the distance between the two tones. This is 3/2 : 4/3 = 9/8, i.e. a major second. Although 8 is a relatively high denominator, which may interfere with the resonance with other scale tones, both the 8 of the second and 2 of the fifth fit the very important octave very well. Also, both the fourth and the fifth have unbeatably low numerators and denominators, which has a favourable impact on the mixing ratios for further scale tones.

In other words: the fourth and the fifth are a perfect pair for resonance – at least mathematically. But does this also sound good?

How does the combination sound in our subjective perception?

Naturally, this is not solely about mathematics. The mental world, our subjective perception, determines whether we like a certain type of music and how we receive it. If you sound the fundamental tone along with the fourth, the fifth and the octave, you can hear what we have calculated: the resonance of the four tones is pure. Indeed, the combination even sounds rather banal, and we may miss the pep that dissonances introduce into the music to which we are accustomed. We also miss the sweetness of the thirds (denominators 5 and 6).

Example 2

We mathematically combine the major second with the minor third, i.e. 9/8 with 6/5: the lcm is 40, the interval between the two tones is 6/5 : 9/8 = 48/45 = 16/15. With the high lcm and the short distance, this pair is a bit more problematical – at least if we pay attention to good resonance and want to avoid any stridency in music.

The first two musical scales found

If you feel like it, you can calculate the lcm and the distance between all the above-mentioned yourself and thus compile a pool of tones in which both aspects are optimised and as much resonance as possible can develop. Of course you also want to select more than just three of four tones for a musical scale. What about five?

The two musical scales with the strongest resonance that can be found in this way are remarkable – both of them are very well-known musical scales:

1 – 9/8 – 5/4 – 3/2 – 5/3 – 2
1 – 6/5 – 4/3 – 3/2 – 9/5 – 2

Or with the fundamental tone C:

C – D  – E – G –  A  –  C
C – Es – F – G – Bb – C

Pentatonic scales

These are two pentatonic scales, i.e. two musical scales with five tones (the C occurs twice but is only counted once). It is not really surprising that both musical scales are good old friends – they are none other than the major and minor pentatonics.

Nor does it come as a surprise that both these musical scales occur in practically all the world’s cultures from the rain forest to all the advanced civilisations, either in their pure form or else as the basic structure of more sophisticated musical scales.

Theoretical and mathematical considerations have led us to postulate these two musical scales which are not only well-known worldwide but are easy to understand for everybody and felt to be catchy by everyone, including small children.

In my view, this is not an accident. It looks as if considerations so far are highly compatible with observed reality.

In the following post, you can find a resonance analysis of the five standard pentatonics.

This is a post about the theory of the three worlds.

What is this about?

According to the theory of the three worlds, mathematics (ideal world) plays a part in physical processes (physical world). Without our subjective perception (mental world), however, we would not be able to notice any of this. I examine the way in which these very different worlds converge in reality with the example of musical scales. There are some riddles here, for instance why human cultures have created thousands of different musical scales, but every one of them uses the octave.

This constancy of the octave can easily be explained by resonance, which in the case of the octave is particularly striking because it corresponds to a mathematical ratio of 2:1. The higher tone of the octave vibrates with twice the frequency of the fundamental tone – an obvious example of how physics, mathematics and subjective perception come together.

In the preceding post I examined whether, with the help of mathematical considerations, we can find further intervals which occur in real musical scales. With only a few mathematical criteria, we found a first pool of intervals which have a high degree of affinity to resonance, i.e. the musical scale tone and the fundamental tone are in a frequency ratio which very easily produces a strong resonance.

Criteria for musical scale tones

Tone range

All musical scales known to me are situated within the range of an octave. This alone is amazing, and we have seen that all three worlds are involved in their creation.The crucial factor for the musical scale tones is their frequencies (f). What is decisive is not the absolute height of the frequency, but only its relative height in comparison with other tones. Below, the number 1 will denote the frequency of the fundamental tone and the number 2 the (doubled) frequency of the octave. All the musical scale tones must be situated between the fundamental tone and the octave; in mathematical terms, this means for the relative frequency f_(ST)of the scale tone (ST) in relation to the fundamental tone:

    1 ≤ f_(ST) ≤  2

2.  Resonance

The physical precondition for resonance to occur is that two frequencies are in a “rational” ratio. In number theory, “rational” describes a number which can be written as a fraction of two integers. In other words: f₂ = m/n f₁ (m andn are integers, f₁ and f₂ are the two frequencies). We now hypothesise that a musical scale tone (ST) is preferably in a ratio (M/N) to the fundamental tone (FT) in which a resonance can develop. In mathematical terms, this is expressed as follows:

    f_(ST)  =  m/n   f_(FT)

This precondition is part of the physical and mathematical worlds and, independently of subjective and cultural perception, a generally valid physical precondition for resonance, also in the non-acoustic sphere.If calculating with interval fractions is new to you, I would like to recommend the annexes, in which the calculation processes and their backgrounds are described in detail.

3.  Strong resonance

A resonance does not always occur equally quickly and equally strongly. Some intervals can therefore develop a resonance more quickly and more strongly than others. I hypothesise that a resonance is the stronger, the smaller m and n are, and I have examined, starting from number 1, what intervals we obtain with as small values as possible for m and n.Surprisingly, it turns out that all the small denominators up to 5 result in musical scale tones which we already know as the most important ones in our traditional European musical scales.The search also reveals that the absolute height of m and n is not the sole determining factor; rather, it comes down to the prime numbers which result from the integer factorisation of m and n. Here it turns out again that among the prime numbers, 5 is also the limit for the numerator.  With this in mind 6, 8 and 9, which are not prime numbers, can be factorised (6=2×3, 8=2×2×2 und 9=3×3) and used for resonances. 7, however, which is a prime number, cannot be factorised and is therefore already too high for m and n in practice.

  m and n should be as small as possible,

Or more precisely: In the integer factorisation of m and n, 5 should be the highest number.

Why integer factorisation? – The musical scale tone does not exist on its own, i.e. it should not only have a resonance in relation to the fundamental tone, but also in relation to the other musical scale tones. This results in compound resonances, mathematically speaking in fractions, in which numerator and denominator can often be reduced. This quickly turns an 8 into a 4, a 15 into a 3, and we again have very small m and n values. Examples will follow.

4. Further criteria

Resonance is not the only requirement for attractive musical scales. Musicians and listeners must also be able to distinguish between the tones. This is easier if there are not too many tones and if they are not too close together. These are not mathematical requirements, nor have they anything to do with resonance. The origin of this demand on a musical scale has something to do with our reception, i.e. with what we are able to perceive – that is, our mental world. With regard to this, our perception depend on the physics of our inner ear and on the physics of our brain. These criteria are thus a demand from the mental world, on the basis of the physical world. Evidently, all three worlds are involved in the creation of the many thousand different musical scales. The following are criteria that are not related to resonance:

4a) The number of the musical scale tones must not be too high.

4b) The musical scale tones must not be too close to each other.

Neither the number of tones nor their minimum distance from each other are the same in every culture. Besides resonance, there are further principles in music, namely that of interference and the higher/lower principle. If the tones are close to each other, music-related training provided by cultural experience may make precisely such tones interesting. However, this does not happen across the whole octave range of the musical scale, for if tones are very close to each other, the overall number of tones in the scale must still not become excessive. The distance between other tones must occasionally be wider again. A musical scale with quarter tones across the whole octave is conceivable but is unlikely to become prevalent in practice.Besides interferences and the higher/lower principle, there is a further principle, the variety principle. This has neither a mathematical nor a physical basis, but a mental one. If everything is the same, things become boring – and this also applies to the distances within a musical scale. This is why we do not experience the whole tone musical scale, which solely consists of identical intervals, as particularly exciting. Yet in combination with other scales with more variants, it is precisely that same whole tone musical scale which can provide an interesting contrast. Pieces of music that would only use whole tone musical scales would not be interesting for long. We thus have a further criterion which is not related to resonance:

4c) The distances in the musical scale should not all be identical.

4d) Fundamental tone principle:

The fundamental tone is the tone which holds the musical scale together. We will have a closer look at this in the section about ecclesiastical modes. As a consequence of the fundamental tone principle, we will always relate the musical scale tones to the fundamental tone.

We compare all the musical scale tones through the fundamental tone.

With the help of these conditions, we will examine our pool of intervals from the preceding post and filter out some first musical scales. Not surprisingly, they are musical scales which do not only have a simple mathematical structure, but also exist worldwide. They are certain pentatonic scales which are not only in use in their pure forms around the globe, but are also contained as a basic structure in more complex musical scales, such as our standard major scale. Firstly, we will have a look at the most resonant musical scales.

Here you can find an overview of the texts about the theory of the three worlds.

The series of overtones

As we know, the octave is the first overtone. The physical phenomenon of resonance has helped us understand the role played by the overtones: in the physical world, vibrating media such as strings or pipes can vibrate with their basic frequency, but also with an integral multiple of this frequency. In this way the octave results as the first integral multiple of the basic frequency – i.e. by the fact that its frequency is doubled.

It would now be obvious to add the further overtones, which are also integral multiples of the basic frequency, and to explain the single notes of the musical scales in this way.

Fig. 1: The fundamental tone and the first four harmonics

Fig. 1 shows how a string vibrates and how the octave and further overtones are added. Whereas the fundamental tone vibrates with precisely one “belly”, the overtones vibrate with two, three, four and more bellies. If we start with the fundamental tone C, this will result in the following series of overtones:

Fig. 2: Overtone series ranging from the fundamental tone C (note 1) to c“‘ (note 16)

The musical scale works in a closed frequency range

Resonance explains the overtone series, including the octave. How, though, does a musical scale come about, which is meant to fill the narrow range between the fundamental tone and the first overtone, i.e. the octave? As mentioned in the previous post, the notes of the musical scales are subject to this constraint whereby they all have to be within the range of an octave. The overtone series, however, leads far beyond an octave.

In addition, Fig 2 also reveals that the distances between the overtones vary a great deal. Whereas initially, they are very far apart, they get closer and closer as the series proceeds. This would be highly impractical for a musical scale to be applied in reality.

We see, however, that the overtones from note 4 onwards, and even more between notes 8 and 16, constitute something like a kind of major scale: c, d, e, (f), g (a), (h), h, c: nearly our major scale, but not exactly, since the tones in brackets (11, 13, 14) don’t quite fit.

The natural “musical scale” of the alphorn

In fact, the musical scale between notes 8 and 16 corresponds to the natural musical scale of the alphorn – including, however, the “off” notes 11, 13 and 14, and without the actually important fourth, namely the f. Nonetheless, the natural tone series of the alphorn – but also only between notes 8 and 16 – is almost something like a natural musical scale in that it packs a reasonable number of notes into the range of an octave, and this even on the basis of resonance.

Yet the overtone series that can be played on the alphorn is still not a real musical scale. Only the musical scale between notes 8 and 16 can be played on this instrument; most notes of the musical scale below this range are missing while above it, there is a confusing array of many more tones, which are increasingly closer to each other. This is not tantamount to a musical scale which repeats itself octave after octave. Additionally, the instrument is somewhat impractical. In order for the notes to be played at a normal pitch, the horn must of necessity be very long. This is different with a violin or a flute, i.e. substantially more practical. With these smaller instruments, however, we cannot achieve the tones of the musical scale as overtones (which would be flageolet tones with the violin, and with the flute pure overblows like with the alphorn), but by means of deliberate mechanical manipulation of the physical object that vibrates, namely the strings of the violin and the air column of the flute.

But do the overtones and resonances play a role in the musical scales nonetheless? – They do! You can read about this in the next post, which explains how a fifth comes about.

This is a post about the theory of the three worlds.