Die Reihe der Obertöne
Die Oktave ist bekanntlich der erste Oberton. Das physikalische Phänomen der Resonanz hat uns geholfen, die Rolle der Obertöne zu verstehen: In der physikalischen Welt können schwingende Medien wie eine Saite oder ein Rohr mit ihrer Grundfrequenz, aber zusätzlich auch mit einem ganzzahligen Vielfachen dieser Frequenz schwingen. Dabei entsteht die Oktave durch das erste ganzzahlige Vielfache – nämlich die Verdoppelung – der Grundfrequenz.
Es wäre nun naheliegend, die weiteren Obertöne, ebenfalls ganzzahlige Vervielfachungen der Grundfrequenz, hinzuzunehmen, und so die Töne der Tonleitern zu erklären.
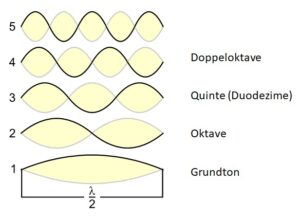
Abb. 1: Grundton und erste vier Oberschwingungen
Abb. 1 zeigt, wie eine Saite schwingt und wie sich Oktave und weitere Obertöne dazu gesellen. Während der Grundton mit genau einem «Bauch» schwingt, schwingen die Obertöne mit zwei, drei, vier Bäuchen usf. Das führt, wenn man vom Grundton C ausgeht zu folgender Reihe von Obertönen:

Abb. 2: Obertonreihe, ausgehend vom Grundton C (Ton 1) bis zum c»‘ (Ton 16)
Die Tonleiter spielt in einem abgeschlossenen Frequenzbereich.
Resonanz erklärt die Obertonreihe, inklusive der Oktave. Wie aber kommt eine Tonleiter zustande, die ja den engen Bereich zwischen dem Grundton und dem ersten Oberton, nämlich der Oktave füllen soll? Wie im Vorbeitrag erwähnt, unterliegen die Tonleitertöne nämlich dieser Einschränkung, sie müssen alle im Bereich einer Oktave liegen. Die Obertonreihe führt aber weit über eine Oktave hinaus.
Zudem zeigt Abb. 2, dass auch die Abstände der Obertöne sehr unterschiedlich sind. Während sie zu Beginn sehr weit auseinander liegen, näheren sie sich im Verlauf immer enger einander an. Dies wäre für eine real zu verwendende Tonleiter sehr unpraktisch.
Wir sehen allerdings, dass die Obertöne ab Ton 4 und noch mehr zwischen Ton 8 und Ton 16 so etwas wie eine Art Dur-Tonleiter bilden: c, d, e, (f), g (a), (h), h, c. Nicht ganz, aber fast unsere Dur-Tonleiter. Die Töne in Klammern (11,13,14) liegen etwas daneben.
Die natürliche «Tonleiter» des Alphorns
In der Tat entspricht die Tonleiter zwischen Ton 8 und Ton 16 der natürlichen Tonleiter eines Alphorns – allerdings mitsamt den «schrägen» Tönen 11,13 und 14 und ohne die eigentlich wichtige Quart, nämlich dem f. Trotzdem ist die Naturtonreihe auf dem Alphorn – aber auch nur zwischen Ton 8 und Ton 16 – fast so etwas wie eine natürliche Tonleiter, indem sie eine vernünftige Anzahl Töne in den Bereich einer Oktave packt, und das erst noch resonanzbasiert.
Doch die auf dem Alphorn spielbare Obertonreihe ist trotzdem keine wirkliche Tonleiter. Man kann damit nämlich die Tonleiter nur zwischen Ton 8 und Ton 16 spielen, darunter fehlen die meisten Tonleitertöne und darüber finden sich verwirrend viele weitere Töne, und zwar immer dichter gelegen. Das entspricht nicht einer Tonleiter, die sich Oktave für Oktave wiederholt. Zudem ist das Instrument etwas unpraktisch. Um Töne in normaler Tonhöhe zu spielen, muss das Horn gezwungenermassen sehr lang sein. Bei Geige oder einer Flöte ist das anders, nämlich wesentlich praktischer. Mit diesen kleineren Instrumenten erreichen wir die Tonleitertöne allerdings nicht als Obertöne (das wären Flageolett-Töne bei der Geige oder reine Überblasungen wie beim Alphorn bei der Flöte), sondern durch bewusste mechanische Manipulation der physikalischen Schwingungsträgers, nämlich der Saiten der Geige und der Luftsäule in der Flöte.
Spielen nun die Obertöne und die Resonanzen bei den Tonleitern trotzdem eine Rolle? – Aber ja! Lesen Sie dazu den Folgebeitrag, der erklärt, wie die Quinte in die Tonleiter kommt, obwohl sie gar kein Oberton ist.
Dies ist ein Beitrag zur Entstehung der Tonleitern