Which of these Preconceptions do you Share?
- Entropy is for nerds
- Entropy is incomprehensible
- Entropy is thermodynamics
- Entropy is noise
- Entropy is absolute
Details
1. Entropy is the Basis of our Daily Lives
Nerds like to be interested in complex topics and entropy fits in well, doesn’t it? It helps them to portray themselves as superior intellectuals. This is not your game and you might not see any practical reasons to occupy yourself with entropy. This attitude is very common and quite wrong. Entropy is not a nerdy topic, but has a fundamental impact on our lives, from elementary physics to practical everyday life.
Examples (according to W. Salm1)
- A hot coffee cup cools down over time
- Water evaporates in an open container
- Pendulums that have been knocked remain stationary after a while
- Iron rusts
- Magnets become weaker after some years
- Lessons learnt are forgotten
- Combed hair becomes dishevelled
- White shirts become stained
- Rocks crumble
- Radioactive elements decay
So there are plenty of reasons to look into the phenomenon of entropy, which can be found everywhere in everyday life. But most people tend to avoid the term. Why is that? This is mainly due to the second preconception.
2. Entropy is a Perfectly Understandable and Indispensable Fundamental Concept
It is true, that at first glance, entropy is rather confusing. However, entropy is only difficult to understand because of persistent preconceptions (see points 4 and 5, below). These ubiquitous preconceptions are the obstacles that make the concept of entropy seem incomprehensible. Overcoming these thresholds not only helps to understand many real and practical phenomena, but also sheds light on the foundations that hold our world together.
3. Entropy Plays a Role Everywhere in Nature
The term entropy stems from thermodynamics. But we should not be mislead by this. In reality, entropy is something that exists everywhere in physics, chemistry, biology and also in art and music. It is a general and abstract concept and it refers directly to the structure of things and the information they contain.
Historically, the term was introduced not 200 years ago in thermodynamics and was associated with the possibility of allowing heat (energy) to flow. It helped to understand the mode of operation of machines (combustion engines, refrigerators, heat pumps, etc.). The term is still taught in schools this way.
However, thermodynamics only shows a part of what entropy is. Its general nature was only described by C.E. Shannon2 in 1948. The general form of entropy, also known as Shannon or information entropy, is the proper, i.e. the fundamental form. Heat entropy is a special case.
Through its application to heat flows in thermodynamics, entropy as heat entropy was given a concrete physical dimension, namely J/K, i.e. energy per temperature. However, this is the special case of thermodynamics, which deals with energies (heat) and temperature. If entropy is understood in a very general and abstract way, it is dimensionless, a pure number.
As the discoverer of abstract and general information entropy, Shannon gave this number a name, the “bit”. For his work as an engineer at the Bell telephone company, Shannon used the dimensionless bit to calculate the flow of information in the telephone wires. His information entropy is dimensionless and applies not only in thermodynamics, but everywhere where information and flows play a role.
4. Entropy is the Difference between not Knowing and Knowing
Many of us learnt at school that entropy is a measure of noise and chaos. Additionally, the second law of physics tells us that entropy can only ever increase. Thus, disorder should but increase. However, identifying entropy with noise or even chaos is misleading.
There are good reasons for this misleading idea: If you throw a sugar cube into the coffee, its well-defined crystal structure dissolves, the molecules disperse disorderly in the liquid and the sugar shows a transition from ordered to disordered. This decay of order can be observed everywhere in nature. In physics, it is entropy that drives the decay of order according to the second law. And decay and chaos can hardly be equated with Shannon’s concept of information. Many scientists thought the same way and therefore equated information with negentropy (entropy with a negative sign). At first glance, this doesn’t seem to be a bad match. In this view, entropy is noise and the absence of noise, i.e. negentropy, would then be information. Actually logical, isn’t it?
Not quite, because information is contained both in the sugar cube as well as in the dissolved sugar molecules floating in the coffee. In some ways, there is even more information in the individually floating molecules because each has its own path. Their bustling movements contain information. For us coffee drinker, however, the bustling movements of the many molecules in the cup does not contain useful information and appears only chaotic. Can this chaos be information?
The problem is our conventional idea of information. Our idea is too static. I suggest that we see entropy as something that denotes a flow, namely the flow between not knowing and knowing. This dynamic is characteristic of learning, of absorbing new information.
Every second, an incredible amount of things happen in the cosmos that could be known. The information in the entire world can only increase. This is what the second law says, and what increases is entropy, not negentropy. Wouldn’t it be much more obvious to put information in parallel with entropy and not with negentropy? More entropy would then mean more information and not more chaos.
Where can the information be found? In the noise or in the absence of noise? In entropy or in negentropy?
Two Levels
Well, the dilemma can be solved. The crucial step is to accept that entropy is the tension between two states, the overview state and the detail state. The overview view does not need the details, but only sees the broad lines. C.F. Weizsäcker speaks of the macro level. The broad lines are the information that interests us. Details, on the other hand, appear to us as unimportant noise. But the details, i.e. the micro level, contain more information, usually a whole lot more, just take the movements of the water molecules in the coffee cup (micro level), whose chaotic bustle contains more information than the single indication of the temperature of the coffee (macro level). Both levels are connected and their information depends on each other in a complex way. Entropy is the difference between the two amounts of information. This is always greater at the detail level (micro level), because there is always more to know in the details than in the broad lines and therefore also more information.
But because the two levels refer to the same object, you as the observer can look at the details or the big picture. Both belong together. The gain in information about details describes the transition from the macro to the micro level, the gain in information about the overview describes the opposite direction.
So where does the real information lie? At the detailed level, where many details can be described, or at the overview level, where the information is summarised and simplified in a way that really interests us?
The answer is simple: information contains both the macro and the micro level. Entropy is the transition between the two levels and, depending on what interests us, we can make the transition in one direction or the other.
Example Coffee Cup
This is classically demonstrated in thermodynamics. The temperature of my coffee can be seen as a metric for the average kinetic energy of the individual liquid molecules in the coffee cup. The information contained in the many molecules is the micro state, the temperature is the macro state. Entropy is the knowledge that is missing in the macro state but is present in the micro state. But for me as a coffee drinker, only the knowledge of the macro state, the temperature of the coffee, is relevant. This is not present in the micro state insofar as it does not depend on the individual molecules, but rather statistically on the totality of all molecules. It is only in the macro state that knowledge about temperature becomes tangible.
For us, only the macro state shows relevant information. But there is additional information in the noise of the details. How exactly the molecules move is a lot of information, but these details don’t matter to me when I drink coffee, only their average speed determines the temperature of the coffee, which is what matters to me.
The information-rich and constantly changing microstate has a complex relationship with the simple macroinformation of temperature. The macro state also influences the micro state, because the molecules have to move within the statistical framework set by the temperature. Both pieces of information depend on each other and are objectively present in the object at the same time. What differs is the level or scope of observation. The difference in the amount of information in the two levels determines the entropy.
These conditions have been well known since Shannon2 and C.F. Weizsäcker. However, most schools still teach that entropy is a measure of noise. This is misleading. Entropy should always be understood as a delta, as a difference (distance) between the information in the overview (macro state) and the information in the details (micro state).
5. Entropy is a Relative Value
The fact that entropy is always a distance, a delta, i.e. mathematically a difference, also results in the fact that entropy is not an absolute value, but rather a relative value.
Example Coffee Cup
Let’s take the coffee cup as an example. How much entropy is in there? If we only look at the temperature, then the microstate corresponds to the average kinetic energy of the molecules. But the coffee cup contains even more information: How strong is the coffee? How strongly sweetened? How strong is the acidity? What flavours does it contain?
Example School Building
Salm1 gives the example of a lost door key that a teacher is looking for in a school building. If he knows which classroom the key is in, he has not yet found it. At this moment, the microstate only names the room. Where in the room is the key? Perhaps in a cupboard. In which one? At what height? In which drawer, in which box? The micro state varies depending on the depth of the request. It is a relative value.
Because the information entropy is always a difference, the entropy, i.e. the span between overview and details, can always be extended to even more details.
Entropy is a relative value. If we specify it in absolute terms, we set – without explicitly declaring it – a lowest level (classroom, shelf or drawer). This is legal as long as we are aware that the seemingly absolute value only represents the distance to the assumed micro-level.
Statics and Dynamics
Energy and entropy are two complementary quantities that permeate the entire description of nature (physics, chemistry, biology). The two fundamental laws of physics each contain one of the two general quantities E (energy) and S (entropy):
- Law: ∆E = 0 oder: dE/dt = 0
- Law: ∆S ≥ 0 oder: dS/dt ≥ 0
Energy remains constant over time (in a closed system), while entropy can only increase. In other words: energy is a static value and shows what does not change, while entropy is essentially dynamic and shows flows, e.g. in heat machines, in Shannon’s current in telephone wires and whenever our thoughts flow and we learn and think.
Entropy and Time
Entropy is essentially linked to the phenomenon of time by the second law (∆S ≥ 0). While energy remains constant in a closed system (Noether’s theorem), entropy changes over time and increases in a closed system. Entropy therefore knows time, not only heat entropy in particular, but also the much more general information entropy.
Conclusion
- Entropy is a key concept in physics and information theory.
- The term entropy comes from thermodynamics, but the concept of entropy refers to information in general.
The thermodynamical entropy is the special case, information entropy is the general concept.- Everything that happens physically, chemically and in information processing, whether technical or biological, has to do with entropy. In particular, everything that has to do with information flows and structures. In other words, everything that really interests us.
- Entropy is always relative and refers to the distance between the macro and micro levels.
- The macro level contains less information than the micro level
- The macro level contains the information of interest.
- Neither is absolute: the micro level can always be described in more detail. The macro level is defined from the outside: What is of interest? The temperature of the coffee? The concentration of sugar molecules? The acidity? The caffeine content …
- Only the definition of the two states makes it possible to specify the entropy in seemingly absolute terms. However, what counts for entropy is the relative value, i.e. the delta between the two states. This delta, the entropy, determines the flow.
- The flow happens in time.
(Translation: Juan Utzinger)
1 Salm, W: Entropie und Information – naturwissenschaftliche Schlüsselbegriffe, Aulis Verlag Deubner, Köln, 1997
2 Shannon, C.E. und Weaver W: The Mathematical Theory of Information, Illinois Press, Chicago, 1949
See also: What is Entropy?
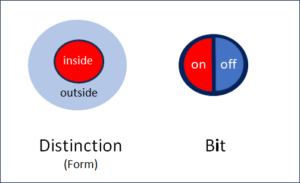

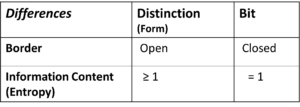

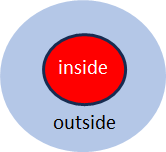
 Fig. 3: Marked (m) and unmarked (u) space
Fig. 3: Marked (m) and unmarked (u) space