«A mathematician may say anything he pleases, but a physicist must be at least partially sane»
(Josiah Williard Gibbs)
«Ein Mathematiker kann sich irgendetwas ausdenken und es innerhalb der Mathematik beweisen. Ob es in der Realität funktioniert, zeigt die Realität.»
(hrs)
Ich mag Mathematik
Ich mag Mathematik. Darin unterscheide ich mich von den meisten meiner Freunde; die meisten wollen möglichst nichts mit Mathematik zu tun haben. Das hat nichts mit der Intelligenz meiner Freunde zu tun – vielmehr bestreiten sie, dass Mathematik für sie persönlich hilfreich sein könnte.
Das ist das eine Lager, quasi das Hauptlager der Menschheit. Im Gegenlager finden sich die Menschen, welche glauben, dass die ganze Welt aus nichts als aus Mathematik besteht. Wenn wir nur die Axiome – z.B. der Mengenlehre – akzeptieren, könnten wir daraus die ganze Welt aufbauen.
Ich verrate kein Geheimnis, wenn ich gestehe, dass ich mich weder zum einen noch zum anderen Lager zähle. Mathematik ist ein unglaublich scharfes Werkzeug und ermöglicht tiefe Erkenntnisse über das Funktionieren unserer Welt. Gleichzeitig ist Mathematik prinzipiell von ihrem Wesen her beschränkt, so kräftig und überzeugend sie in ihrem ureigenen Bereich auch ist.
Die spannende Frage für mich ist: Wie ordnet sich die Mathematik in die Realität ein?
Abgeschlossenes System
Eine charakteristische Eigenheit der mathematischen Welt ist, dass abgeschlossene Systeme untersucht werden, z.B. die Menge der natürlichen Zahlen. Abgeschlossene Systeme können konsequent und logisch untersucht werden, und die gewonnen Aussagen sind deshalb sehr sicher wahr – für das untersuchte System.
Obwohl die Menge der natürlichen Zahlen unendlich ist, ist sie doch abgeschlossen, insofern, als die Grenzen klar sind: für jede Zahl kann ausgesagt werden, ob sie zur Menge gehört oder nicht: 25399275933184 z.B. gehört dazu, nicht aber 1/2, π oder -1 .
Vorteil Mathematik: Die Abgeschlossenheit mathematischer Systeme ist die Basis für die Sicherheit der Aussagen. Weil das System geschlossen ist, können (fast! ← Gödel) alle Aussagen klar auf ihren Wahrheitswert überprüft werden.
Nachteil Mathematik: Die Aussagen gelten aber nur für das geschlossene System. Die reale Welt ist immer offen.
Konsequenz: Mathematische Systeme beschreiben eindrücklich das Verhalten physikalischer Objekte und Systeme. Allerdings sind letztere stets offen. Das stellt uns vor die Aufgabe, die Wahl des passenden mathematischen System sehr sorgfältig zu überprüfen und gegebenenfalls anzupassen. Wahl und Anpassung des mathematischen System erfolgen logischerweise stets ausserhalb des mathematischen Systems.
Abstraktion
Mathematik ist platonisch; d.h. die Elemente der Mathematik sind ausserhalb von Raum und Zeit. Nur so können sie ‚ewig‘ gültig sein.
Physik hingegen beschäftigt sich mit Objekten, die sich innerhalb von Raum und Zeit befinden.
Die Abstraktion (Mathematik) ist immer einfacher als die Verhältnisse (Physik), auf die sie sich bezieht.
Vorteil Mathematik: Mathematische Wahrheiten sind zeit- und ortsunabhängig. Die Wahrheit (Widerspruchsfreiheit) kann innerhalb des Systems (meistens! ← Gödel) bewiesen werden. Sobald eine mathematische Wahrheit einmal mathematisch korrekt erkannt ist, erübrigen sich weitere Diskussionen über ihren Wahrheitswert.
Nachteil Mathematik: Mathematische Aussagen gelten nur innerhalb der Mathematik, d.h. innerhalb der Abstraktion. Gelten sie auch ausserhalb, d.h. in der Realität? Diese Frage kann nicht innerhalb der Mathematik abschliessend beantwortet werden. – Weshalb nicht? Antwort: Die Korrektheit der Schlüsse gilt nur innerhalb der Abstraktion, doch ist die Abstraktion auf die Realität anwendbar? Diese Frage kann eben nicht innerhalb der Mathematik beantwortet werden, da sie die Abstraktion prinzipiell überschreitet.
Die hilfreiche Mathematik und ihre Grenze
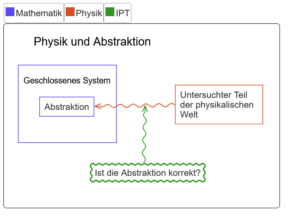
Abb 1:Abstraktion und geschlossenes System
(IPT = Interpretationstheorie)
Die Physik versucht, ihren Stoff in eine mathematische Form zu bringen. Dabei ist sie höchst erfolgreich, was nicht nur für die Leistung der Physiker, sondern auch für die Eignung, Raffinesse und Kohärenz der mathematischen Modelle spricht.
Doch die entscheidende Frage kann nur in der Realität, d.h. von der Physik beantwortet werden, nämlich:
Ist die Abstraktion korrekt, d.h. ist das – immer vereinfachte! – mathematische Modell auch anwendbar? – Diese Frage kann nur ausserhalb von der Mathematik beantwortet werden.