Die beiden Arten von Kodierung in Mengendarstellungen

Ich möchte an den ersten Beitrag zu Zwei Arten von Codierung anschliessen und den Unterschied zwischen den beiden Arten von Kodierung mit Mengen-Diagrammen verdeutlichen, denn ich denke, dass der Unterschied für das Gebiet der Semantik und für die allgemeine Informationstheorie wichtig genug ist, um allgemein verstanden zu werden.

Informationserhaltende Kodierung

Den informationserhaltenden Typus der Kodierung, kann man mit folgendem Diagramm darstellen:

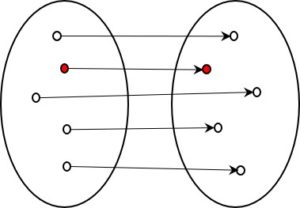
Links sei die ursprüngliche, rechts die kodierte Form. Der rote Punkt könnte links z.B. der Buchstabe A sein, rechts der Morsekode Punkt-Strich. Da es sich um eine 1:1 – Abbildung handelt, findet man von jedem Element rechts sicher wieder zum Ausgangselement links, vom Punkt-Strich des Morsecodes also wieder den Buchstaben A.

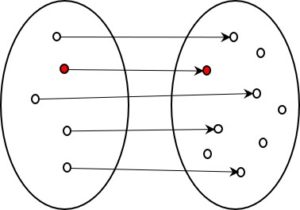
Eine 1:1 Kodierung ist natürlich auch dann informationserhaltend, wenn nicht alle Kodes benützt werden. Da die unbenutzten bei der Kodierung nie entstehen können, spielen sie gar keine Rolle. Von jedem für einen Kode benützten Element der Abbildungsmenge rechts gibt es genau ein Element der Ausgangsform. Der Kode ist dadurch ohne Informationsverlust reversibel, d.h. dekodierbar und die ursprüngliche Form kann für jeden entstehenden Kode verlustfrei wieder hergestellt werden.

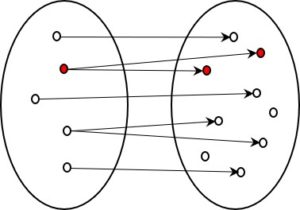
Auch bei einer 1:n – Kodierung kann die ursprüngliche Form verlustfrei rekonstruiert werden. Ein Ursprungselement kann zwar auf verschiedene Weise kodiert werden, doch jeder Kode hat nur ein Ursprungselement. Somit kann der Ausgangswert zweifelsfrei wieder erreicht werden. Auch hier spielt es keine Rolle, ob alle möglichen Kodes (Elemente rechts) gebraucht werden oder nicht, da nicht verwendete mögliche Kodes nie erreicht und somit auch nicht rückübersetzt werden müssen.

Bei allen bisher dargestellten Kodierverhältnissen (1:1 und 1:n) kann die ursprüngliche Information wieder vollständig rekonstruiert werden. Dabei kommt es nicht darauf an, ob 1:1 oder 1:n, und ob alle möglichen Kodes verwendet werden oder manche auch frei bleiben. Wichtig ist nur, dass jeder Kode immer nur von einem Ursprungselement erreicht werden kann – mathematisch gesprochen handelt es sich bei den informationserhaltenden Kodierungen um linkseindeutige Relationen.

Informationsreduzierende Kodierung

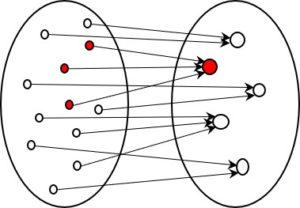
Hier gibt es nun in der Ausgangsmenge mehrere Elemente, die auf den gleichen Kode, d.h. auf das gleiche Element in der Menge der entstehenden Kodes zeigen. Dadurch kann die ursprüngliche Form später nicht mehr rekonstruiert werden. Der rote Punkt in der Abbildungsmenge rechts repräsentiert einen Kode für den es drei unterschiedliche Ausgangsformen gibt. Die Information über den Unterschied zwischen den drei Punkten geht dadurch rechts verloren und kann nicht mehr rekonstruiert werden. Mathematiker sprechen von einer Relation, die nicht linkseindeutig ist. Kodierungen von diesem Typ verlieren Information.

Dies Art Kodierung ist zwar weniger «sauber»,  trotzdem ist sie aber genau diejenige, die uns besonders interessiert, da sie in der Realität für viele Vorgänge typisch ist.