Objekte und Relationen

Als erstes schauen wir eine Menge von Objekten an und überlegen uns, wie viele Verbindungen (Relationen) es zwischen ihnen gibt. Dabei legen wir unser Augenmerk nicht auf die Art der Beziehung zwischen den Objekten, sondern beschränken uns darauf, die Relationen zu zählen. Das ist ganz einfach ist, denn im Prinzip besteht zwischen jeweils zwei Objekten immer genau eine Relation. Auch wenn die zwei Objekte nichts miteinander zu tun haben, ist das eine Information, die etwas aussagt, und somit eine gültige, d.h. aussagekräftige Relation. Wir zählen also die Zahl der möglichen Verbindungen zwischen den Objekten zusammen und vergleichen die Zahl der Objekte mit der Zahl der Relationen.

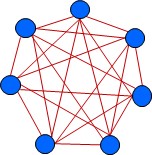
In Abb 1 sehen wir sieben Objekte (blau) und ihre Relationen (rot). Jedes Objekt ist mit jedem anderen Objekt verbunden, in unserem Beispiel also jedes der 7 Objekte mit 7-1 = 6 weiteren Objekten. Insgesamt erhalten wir so 7 *6 / 2 = 21 Relationen. Die allgemeine mathematische Formel dafür ist oder N_R = (N_O² – N_O) / 2. Dabei ist N_R die Zahl der Relationen und N_O die Zahl der Objekte.
Die Zahl der Relationen nimmt, wie wir aus der Formel ersehen können, im Quadrat zur Zahl der Objekte zu. Nicht-mathematisch ausgedrückt:

Es gibt immer viel mehr Relationen als Objekte, und zwar sehr viel mehr!

Hier eine kleine Tabelle mit den Zahlen für Objekte und Relationen:

N_O  N_R
———————-
1    0
2    1
3    3
4    6
5    10
6    15
7    21
8    28
9    36
10     45
100   4950
1000    499’500

Tab 1: Objekte und Relationen

Bei kleinen Zahlen fällt die quadratische Steigerung nicht so auf, bei nur leicht grösseren fällt sie aber schon deutlich ins Gewicht. Wir können uns jetzt schon überlegen, was diese Zunahme in der Praxis bedeutet, schauen uns aber vorher noch die Zahl der möglichen Kombinationen an.

Objekte und Kombinationen

Bei Kombinationen geht es darum, wie mehrere Objekte miteinander kombiniert werden können. Während bei den Relationen eine Relation immer genau zwei Objekte verbindet, können Kombinationen beliebig viele Objekte enthalten, also jede Anzahl Objekte von 1 bis alle (= N_O).

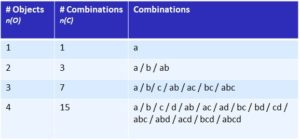
Tabelle 2 zeigt Mengen mit 1 bis 4 Objekten. Die Anzahl der Objekte ist in der ersten Spalte, diejenige der Kombinationen in der zweiten aufgeführt. Die Objekte sind mit Buchstaben (a, b, c ,d) bezeichnet. In der Spalte ganz rechts sind die jeweils möglichen Kombinationen aufgezählt. Bei nur einem Objekt (a) gibt es gerade einmal eine Kombination, die aus genau diesem Element besteht, bei 2 Objekten gibt es 3 Kombinationen und bei 4 Elementen sind es bereits 15. Die Zahl der Kombinationen pro Objekt nimmt also noch stärker zu als vorher die Zahl der Relationen. Die Formel dafür ist: N_C = 2^No – 1.

Bei den Relationen wird N_O quadriert, während es bei den Kombinationen im Exponenten vorkommt. Dies bewirkt eine noch grössere, nämlich eine exponentielle Steigerung. Die Zahl der möglichen Kombinationen steigt dabei exponentiell zur Zahl der vorhandenen Objekte. Bei 10 Objekten gibt es bereits 1023 Kombinationen, bei 100 Objekten sind es in der Tat 1’267’650’600’228’229’401’496’703’205’375 Kombinationen.

Die Zahl der Kombinationen steigt somit sehr schnell extrem stark an.

Diese exponentielle Zunahme ist die Basis der kombinatorischen Explosion.

Kombinatorische Explosion

Nehmen wir an wir haben verschiedene Objekte mit verschiedenen Eigenschaften, z.B.:

4 Formen: rund, quadratisch, dreieckig, sternförmig.
8 Farben: rot, orange, gelb, grün, blau, braun, weiss, schwarz.
7 Materialen: Holz, PVC, Aluminium, Karton, Papier, Glas, Stein.
3 Grössen: klein, mittel, gross.

Diese vier Klassen mit ihren insgesamt 22 Eigenschaften können wir nun beliebig kombinieren, ein Objekt kann also z.B. dreieckig, grün, mittelgross und aus PVC sein. Wie viele verschiedenartige Objekte können wir mit den 22 Eigenschaften nun insgesamt unterscheiden?

Die Antwort ist, dass aus jeder der vier Klassen (Form, Farbe, Material, Grösse) je eine Eigenschaft unabhängig gewählt werden kann. Das ergibt insgesamt 4x8x7x3 = 672 Möglichkeiten der Kombination. Mit 22 Eigenschaften können also 672 verschiedene Objekte beschrieben werden. Für jede weitere Klasse multipliziert sich die Zahl der Möglichkeiten.

Schon nach wenigen zusätzlichen Klassen explodiert die Zahl der möglichen Kombinationen regelrecht.

Das ist die kombinatorische Explosion. Sie spielt in ganz vielen Situationen eine entscheidende Rolle.

---

Nachtrag vom 23.3.2020

Beispiele für exponentielles Wachstum:
– Epidemien
– Zins und Zinseszins
– Gewisse Treibhausgase
– Kettenreaktionen, z.B. in nuklearen Explosionen
– «Going viral» im Internet
– «Going viral» von Unternehmen
– Popularitätskurven von Showstars und Politikern

Grenzen des Wachstums:
Da in der Realität kein unbegrenztes Wachstum möglich ist, stösst ein exponentielles Wachstum immer an Grenzen, weil entweder die Ressourcen für weiteres Wachstum erschöpft sind, oder kein Raum für weitere Ausbreitung mehr vorhanden ist.  Oft bricht dann das Wachstum plötzlich und unerwartet ab.

Lineares und exponentielles Wachstum:
Wir tendieren dazu, Wachstum als linear, d.h. als gleichmässig anzusehen. Wachstum ist aber in vielen Gebieten exponentiell, was wir oft ausblenden. Weshalb ist das so? Wenn wir nur einen kleinen Zeitraum eines exponentiellen Wachstums anschauen, erscheint die Kurve linear, erst bei einer längeren Betrachtungsweise zeigt sich die exponentielle Steigung. Die Steigung kann zu Beginn sogar sehr  klein sein und  quasi vernachlässigbar erscheinen, doch das ist eine Täuschung, wenn das Wachstum exponentiell ist.