Dieser Beitrag setzt Paradoxe Logikkerne (Teil 1) fort
«Draw a Distinction»
Mit diesen Worten führt Spencer-Brown den elementaren Baustein seiner formalen Logik ein: «Draw a Distinction» – «Zieh eine Unterscheidung». Abbildung 1 zeigt dieses sehr einfache Element der Unterscheidung oder Distinction, den formalen Baustein von Spencer-Browns Logik:

Abb 1: Die Form der Unterscheidung von Spencer-Brown
Eine extreme Abstraktion
In der Tat besteht seine Logik ausschliesslich aus diesem Baustein. Spencer-Brown ist damit eine Abstraktion gelungen, die abstrakter ist als alles, was Mathematiker und Logiker bisher gefunden hatten.
Was ist mit dieser Form nun gemeint? Spencer-Brown zielt auf einen elementaren Prozess, nämlich das ‚Ziehen einer Unterscheidung‘. Dieser elementare Prozess teilt nun die Welt in zwei Teile, nämlich den Teil, der innerhalb der Unterscheidung liegt, und den Teil ausserhalb.
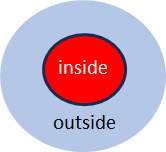
Abb. 2: Visualisierung der Unterscheidung
Die Teilung der Welt
Abbildung 2 zeigt, was das formale Element von Abb 1 meint: eine Teilung der Welt in das Unterschiedene (inside) und alles andere (outside). Der Winkel von Abb. 1 wird also – gedanklich – zum Kreis, der alles einschliesst, was gemeint, also unterschieden («draw a distinction») ist.
Die Winkelform von Abb. 1 meint also den Zirkel von Abb. 2, der alles umfasst, was gemeint ist.
Perfekte Beinhaltung
Weshalb aber zeichnet Spencer-Brown seinen elementaren Baustein als offenen Winkel und nicht als geschlossenen Kreis, obwohl er die Geschlossenheit meint, indem er ausdrücklich sagt: «Distinction is perfect continence», der Unterscheidung also eine perfekte Beinhaltung zuweist. Dass er trotzdem die Beinhaltung als Winkel zeigt, wird später klar werden, und sich als eine von Spencer-Browns genialen Entscheidungen erweisen. (mehr dazu im iommenden Beitrag «Imaginärer Logikwert»)
Unterscheidung von Markiert und Unmarkiert
Zudem ist es möglich, die Innenseite und die Aussenseite zu benennen, als den markierten (m=marked) und den unmarkierten (u=unmarked) Raum und diese Benennungen später in grösseren Kombination von Unterscheidungen zu verwenden.
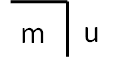
Abb. 3: Marked (m) und unmarked (u) space
Kombinatierte Unterscheidungen
Um den Baustein in grösseren Logikaussagen zu verwenden, kann er nun auf verschiedene Weisen zusammengestellt werden.
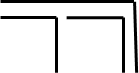
Abb. 4: Drei kombinierte Formen der Unterscheidung
Abbildung 4 zeigt, wie Unterscheidungen auf zwei Arten miteinander kombiniert werden können, entweder als Aufzählung (seriell) oder als Etagierung, indem über Unterscheidungen weitere Unterscheidungen gestellt werden. Spencer Brown arbeitet mit diesen Kombinationen und leitet – ganz Mathematiker – verschiedene Schlüsse und Beweise aus wenigen Axiomen und Kanons ab. Er baut auf diese Weise ein eigenes formales mathematisch-logisches Regelwerk auf. Die Ableitungen und Beweise müssen uns hier nicht vordringlich interessieren, sie zeigen aber, wie sorgfältig und mathematisch-penibel Spencer-Brown seinen Formalismus entwickelt.
Re-Entry
Das Re-Entry, der Wiedereintritt ist nun das, was uns zum Paradox führt. Es ist nun in der Tat so, dass Spencer-Browns Formalismus es möglich macht, den Formalismus echter Paradoxe, wie z.B des Barbierparadoxes auf ganz einfache Weise zu zeichnen. Das Re-Entry wirkt wie ein leuchtender Edelstein (sorry für die poetische Ausdrucksweise), der in logischen Netzen eine ganz spezielle Funktion übernimmt, nämlich die Verknüpfung von zwei logischen Ebenen, einer Basisebene und ihrer Metaebene.
Der Trick dabei ist, dass auf beiden Ebenen die gleiche Unterscheidung getroffen wird. Dass es sich also um die gleiche Unterscheidung handelt, aber auf zwei Ebenen, und dass sich diese eine Unterscheidung auf sich selber bezieht, von der einen Ebene auf die andere, von der Metaebene auf die Basisebene. Das ist die Form der Paradoxie.
Beispiel Barbierparadox
Wir können nun das Barbierparadox mit Hilfe der Form von Spencer-Brown notieren:

Abb. 5: Unterscheidung der Männer des Dorfes, die
sich selber (S) oder nicht selber (N) rasieren
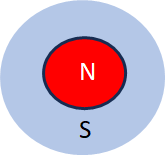
Abb. 6: Notation von Abb. 5 als perfekte Beinhaltung
Abb. 5 und Abb. 6 zeigen das gleiche, nämlich die Unterscheidung der Männer des Dorfes in solche, die sich selber rasieren und die anderen, die das nicht tun.
Wie kommt nun der Barbier hinein? Nehmen wir an, er ist eben aufgestanden und noch unrasiert. Dann gehört er zur Innenseite der Unterscheidung, also zur Gruppe der unrasierten Männer N. Kein Problem für ihn, er rasiert sich schnell, frühstückt und geht dann an die Arbeit. Jetzt gehört er zu den Männern S, die sich selber rasieren, er muss sich also nicht mehr rasieren. Das Problem stellt sich erst am nächsten Morgen. Jetzt gehört er ja zu den Männern, die sich selber rasieren – also muss er sich nicht rasieren. Unrasiert, wie er ist, muss er sich aber jetzt rasieren. Sobald er sich aber rasiert, gehört er zur Gruppe der Selberrasierer, muss sich also nicht rasieren. So wechselt der Barbier von einer Gruppe in die andere. Es stellt sich das typische Oszillieren des Barbierparadoxes – und auch aller anderen echten Paradoxien ein, die alle oszillieren.
Wie entsteht das Paradox?
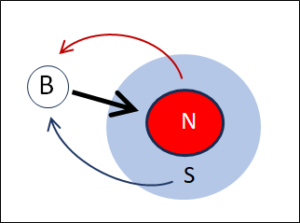
Abb. 7: Der Barbier (B) rasiert alle Männer, die sich
nicht selber rasieren (N)
Abb. 7 zeigt als Basis die Unterscheidung der Männer N (rot) und S (blau). Das ist die Basisebene. Nun kommt der Barbier (B) hinein. Auf einer logischen Metaebene wird ausgesagt, dass er die Männer N rasiert, in Abb. 7 durch den Pfeil symbolisiert.
Das Paradox entsteht zwischen der Basis- und der Metaebene. Dann nämlich, wenn gefragt wird, ob der Barbier, der ja auch ein Mann des Dorfes ist, zur Menge N oder zur Menge S gehört. Mit anderen Worten:
→ Ist B ein N oder ein S ?
Wenn B ein N ist, dann rasiert er sich (Abb. 7). Dadurch wird er zu einem S, also rasiert er sich nicht. Dadurch wird er zum N und rasiert sich. Das ist das Paradox und seine Oszillation.
Wie entsteht sie? Indem die beiden Ebenen verknüpft werden. Der Barbier ist ein Element der Metaebene, aber gleichzeitig ein Element der Basisebene. Der Barbier B ist auf der Metaebene ein handelndes Subjekt, auf der Basisebene aber ein Objekt. Die beiden Ebenen sind verknüpft über eine einzige Unterscheidung, doch B ist einmal Subjekt und sieht die Unterscheidung von aussen, doch gleichzeitig ist er auch ein Objekt dieser Unterscheidung, und wird dadurch als N oder S markiert. Das ist das Re-Entry.
Das Re-Entry ist die logische Form der Paradoxie. Spencer-Browns Leistung besteht darin, dass er diese Form radikal einfach darstellt und sie formal maximal abstrahiert. Sie reduziert sich auf eine einzige Unterscheidung, die auf zwei Ebenen gelesen wird, einmal grundsätzlich (B ist N oder S) und dann als Re-Entry, wenn überlegt wird, ob B sich selber rasiert.
Das Paradox entsteht durch das Re-Entry plus eine Negation: Er rasiert die Männer, die sich nicht selber rasieren. Re-Entry und Negation gehört zwingend dazu, um ein echtes Paradox zu generieren. Sie lassen sich bei allen echten Paradoxien nachweisen, beim Barbierparadox, beim Lügnerparadox, beim Russelparadox usw.
Der Kern von jedem echten Paradox
Georg Spencer-Browns Leistung besteht darin, dass er das Paradox auf seinen essentiellen formalen Kern reduziert hat:
→ Eine (einzige) Unterscheidung mit Re-Entry und Negation.
Dieser Kern kann in jedem echten Paradox gefunden werden. Spencer-Brown’s Entdeckung von Unterscheidung und Re-Entry hat nun weitrechende Konsequenzen bezüglich Logik, aber auch weit über die Logik hinaus.
Darauf will ich gerne eingehen. Als nächstes möchte ich aber die Distinction, d.h. die Unterscheidung von Spencer-Brown als Logikelement mit einem anderen Logikelement vergleichen, das Ihnen sicher bestens bekannt ist, nämlich dem Bit.
Fortsetzung: Unterscheidung (nach Spencer-Brown) und Bit
Frühere Beiträge zur Selbstreferenzialität und zum Re-Entry:
Selbstreferentialität bringt klassische logische Systeme wie FOL oder Boolsche Algebra zum Absturz.
Mehr zum Thema Logik -> Übersichtsseite Logik