Die zehn resonantesten Töne innerhalb der Oktave
Wir untersuchen in dieser Textserie die Tonleitern unter dem Aspekt der drei Welten. Alle drei Welten sind mitbeteiligt, wie wir das z.B. gesehen haben bei der Beantwortung der Frage, weshalb die Tonleitern aller Musikkulturen immer genau eine Oktave abdecken. Nur mathematisch oder physikalisch lässt sich das nicht erklären. Unter Hinzunahme der dritten Welt, nämlich unserer mentalen Welt, wird die Bedeutung der Oktave einleuchtend.
Auch die Auswahl der in der Tonleiter verwendeten Töne wird über das Phänomen der Resonanz von allen drei Welten bestimmt, wie wir in den Vorbeiträgen gesehen haben. Schauen wir jetzt an, wie die zehn resonantesten Töne im Verlauf der Tonleiter-Oktave angeordnet sind. Wir werden dabei sehen, dass es in der Anordnung Lücken gibt, und uns dann überlegen, welche Konsequenzen wir daraus ziehen können.
Hier also nochmals die 10 Töne. (In Tabelle 1 sind zwar 11 aufgeführt, aber der Grundton und die Oktave zählen als ein Ton, da die Oktave sowohl der höchste Ton der aktuellen, als auch gleichzeitig der Grundton der nächsthöheren Oktave ist, in der sich die Tonleiter ja wiederholt).
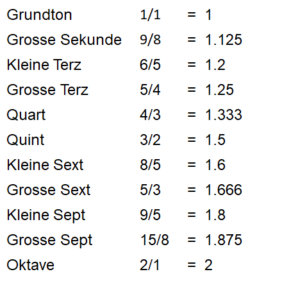
Tab. 1: Der Grundton und die zehn resonantesten Intervalle in einer Oktave
In Tabelle 1 finden sich in der mittleren Spalte die Brüche, welche das Verhältnis des Tonleitertons zum Grundton angeben, bei der Quinte z.B. beträgt die Frequenz das 3/2-fache der Grundfrequenz. Ganz rechts habe ich diese Brüche als Dezimalzahlen angegeben, damit man sie besser vergleichen kann. Die Zahlen bewegen sich selbstverständlich zwischen 1 (Grundton) und 2 (Oktave).
Anordnung der zehn Töne
Um zu sehen, wie sich die zehn Töne innerhalb der Oktave verteilen, nehmen wir die Frequenzen der Töne und vergleichen sie mit der Frequenz des Grundtons. Dies Frequenzverhältnisse finden sich in Tabelle 1 in der rechten Spalte. Diese Zahlen habe ich in die Abbildung 1 übertragen und Sie sehen, wie sich die Frequenzverhältnisse linear anordnen.
So sieht die Anordnung der Intervalle von Tabelle 1 aus:

Abb. 1: Frequenzverhältnisse der potentiellen Tonleitertöne (Tab. 1) in linearer Darstellung. Die Intervalle sind hier von C aus gedacht, d.h. C = Grundton.
In Abb. 1 fällt sofort auf, wie unregelmässig die Anordnung ist. Die Verteilung weist vier grössere Lücken auf, nämlich zwischen C-D, F-G, A-B und H-C. Subjektiv wirkt die Verteilung auch nicht masstabsgetreu, z.B. ist der Abstand zwischen dem Grundton und der Quart (C-F) viel kleiner als der zwischen der Quint und der Oktave (G-C). Wir empfinden aber beide Intervalle als die gleichen, nämlich als zwei Quarten, denn auch zwischen G und C ist der Abstand eine Quarte, genau wie zwischen C und F. Trotzdem ist es von G zu C in Abbildung 1 viel weiter als von C zu F. Weshalb entspricht der wahrgenommene Abstand nicht dem wirklichen Frequenzverhältnis? – Die Antwort liegt wieder im exponentiellen Verlauf der Frequenzen (physikalische Welt), der nicht unserer linearen Empfindung (mentale Welt) entspricht. Wir müssen deshalb die Frequenzen logarithmisch notieren und kommen so zu einer Darstellung, die unserer subjektiven Wahrnehmung entspricht:

Abb. 2: Frequenzverhältnisse der Abb. 1 in einer logarithmischen Darstellung.
Wir sehen, dass in Abb. 2 die Abstände unserer subjektiven Empfindung masstabsgetreuer entsprechen. So ist im Gegensatz zu Abb. 1 z.B. zwischen C und F der gleiche Abstand wie zwischen G und C, was wir als zutreffend empfinden, nämlich beidesmal als eine Quarte. Auch die anderen Abstände entsprechen unserer Empfindung.
Weiterhin sieht die Anordnung jedoch unregelmässig aus und es bestehen Lücken. Diese haben sich nun aber ebenfalls verschoben. Die Lücke C-D ist grösser geworden, während H-C kleiner geworden ist. Wirklich auffällig sind die beiden Lücken C-D und F-G. Können wir da etwas tun? Es geht wieder um die mentale Welt. Wir empfinden die Lücken wirklich. Können wir wieder unsere Resonanzüberlegungen zu Hilfe ziehen, um die Lücken zu füllen? Im nächsten Beitrag erkläre ich wie das geht.
Wir können nämlich Intervalle auch kombinieren. Das kombinierte Intervall weist dann auch noch eine gewisse Resonanz auf, diese ist jedoch meist schwächer als bei den beiden Ausgangsintervallen. Deshalb sind diese Intervalle in den Tonleitern etwas weniger beliebt. Mehr in der Fortsetzung.
Die ist ein Beitrag zur Entstehung der Tonleitern.