Schlagwort-Archive: Bit

Information, Künstliche Intelligenz, Logik

Die Wurzeln der KI

Hinterlassen Sie einen Kommentar

Wie beeinflusst die Geschichte der KI ihre Zukunft?

Heute ist mit KI die Methode der  Neuronalen Netze gemeint. Dies ist eine ganz spezielle Form der Maschinenintelligenz, die auf der statistische Auswertung von riesigen Datenmengen beruht. Der geschichtliche Blick sieht sich neben dieser sehr erfolgreichen, statistischen Methode die Maschinenintelligenz ganz allgemein. Wie hat sich diese entwickelt? Was sind ihre Wurzlen. Wohin führt sie?

Heutige, offene Denker stellen der ‹traditionellen› Vergangenheit gern eine neue ‹originelle› Zukunft gegenüber. Doch wir wissen alle nicht, was in der Zukunft wirklich sein wird – auch wenn ich selber darüber gern spekuliere.

Die Tradition ist für die Zukunft nützlich, wenn man sich eingesteht, dass Sie folgende vier unterscheidbare Elemente enthält:

  1. Ungelöste Fragen, die heute beantwortet werden können und den Boden der Zukunft bilden
  2. Erkannte Fehler, die in der Zukunft korrigiert werden können
  3. Verschmähte Perlen, die von der Gegenwart ignoriert, aber in Zukunft wieder Bedeutung erlangen können.
  4. Bleibendes, das auch in Zukunft gilt

Diese unterschiedlichen Elemente der Tradition zu unterscheiden ist nicht einfach, doch genau darum geht es.

Wissenschaftsgeschichte

Wissenschaftsgeschichte hat mich seit der Schule interessiert. So enthält zum Beispiel die Medizingeschichte viele verblüffende Wendungen, was angewendeten Praktiken und die ihnen zugrundelegenden Erklärungen betrifft. Das ist faszinierend. Im Medizinstudium hat mich die Geschichte der Medizin brennend interessiert, die voll ist von Erneuerungen, Paradigmenwechseln und ideologischen Vorgaben. Sehr spannend, und den Ärzten und der Allgemeinheit kaum bekannt.

Ganz ähnlich steht es um die Geschichte der Informationswissenschaft. Auch hier sind die divergierenden Elemente a) bis d) deutlich zu erkennen, doch auch diese Geschichte ist der Allgemeinheit und den Fachspezialisten kaum bekannt. Die IT-Geschichte wird von den aktuellen Diskussionen um die AI und ihren Einfluss auf unsere Gesellschaft völlig überblendet. Dabei hilft erst der Blick auf die Geschichte, die heutigen Herausforderungen in einem nüchternen Blick zu sehen.

Informationswissenschaft

Die Geschichte der Informationswissenschaft kann bis zu den Syllogismen von Aristoteles zurückverfolgt werden. Rechenmaschinen und ihre Theorie finden sich z.B. im Mittelalter beim missionierenden Franziskaner und Logiker Ramon Lullus und im Barock beim Universalgelehrten Gottfried Wilhelm Leibniz.

In der Mitte des 20. Jahrhundert finden wir dann eine wirkmächtige Entwicklung, eine eigentliche ‹kybernetische Welle‹ mit vielen Facetten und Köpfen, die am Ursprung der heutigen IT-Explosion steht.

Zur Kybernetischen Welle gehört neben vielen anderen der Ingenieur Claude Shannon, der für die Telefongesellschaft Bell das Leibniz’sche Bit aufgegriffen und in die Berechnungen der Telefonsignale eingeführt hat, oder der Praktiker Zuse, der in Berlin den ersten funktionierenden Computer im heutigen Sinn gebaut hat. Zur  vielköpfigen ‹kybernetischen Welle› gehören unter anderen der Antroposoph und Logiker Gregory Bateson, der Österreich-Amerikaner Heinz von Förster, der Mathematikerschreck George Spencer-Brown, der britische Radarpionier Donald MacKay und die enthusiastische amerikanische Pionierszene der Kybernetik der 50-er und 60-er Jahre,  eine bemerkenswerte Kombination von intellektuellen Hippies und an neuen Techniken interessierten Nachrichtenoffizieren, die sich damals z.B. in den Macy-Konferenzen fanden, und die zusammen die gesamte heutige IT inklusive AI recht eigentlich begründet haben.

Zur kybernetischen Welle gehören für mich aber auch Nicht-Informatiker wie der Schriftsteller Stanislaw Lem, der in den «Sterntagebüchern» einen raumfahrenden Baron von Münchhausen auftreten lässt, Ijon Tichy genannt. In den fiktiven Reisebeschreibungen, die zwischen 1957 und 1971 entstanden, werden nicht zuletzt logische Probleme, insbesondere solche der KI, exemplarisch behandelt. Klügere Literatur zu Logik und Auswirkung der KI habe ich nirgendwo gefunden.

Auch der Mathematiker und Physiker Roger Penrose muss erwähnt werden, der zur Kosmologie der Entropie – der physikalischen Dimension von Information – geforscht hat und dessen Buch ‹Emperors New Mind‹ im Jahr 1989 als Kritik an einer überbordenden KI-Gläubigkeit entstand, im Endergebnis aber einen ausführlichen und fundierten Einblick in das physikalische Wissen am Ende des 20. Jahrhunderts ermöglicht.

Die erwähnten Kybernetiker, Philosophen, Naturwissenschaftler und Schriftsteller sind die praktischen Begründer und Vordenker der KI. Sie ringen stets auch um philosophischen Fragen. Sie beschäftigen sich nicht zuletzt intensiv mit der Fragen der Logik – geschlossen oder doch offen? – und der Rolle der KI, also der Frage, wie Intelligenz und Maschinen vereinbar sind.

Was bringt nun die Zukunft?​

Wir können die Zukunft gestalten, indem wir auf die oben erwähnten Elemente der Vergangenheit reagieren und versuchen …

  1. zu antworten: In den ungelösten Fragen der Verganenheit liegt die Zukunft
  2. zu erkennen: Die blinden Flecken und Tabus der Vergenheit.
  3. zu schätzen: Nicht alles von früher ist schlecht.
  4. zu behalten: Was ist der bleibende Kern?

 

Information

Entropie: Schlüssel zur Informationstheorie

Entropie ist mehr als Wärmelehre

Der Begriff Entropie stammt ursprünglich aus der Wärmelehre und ergänzt dort den Begriff der Energie. Entropie ist aber viel mehr, nämlich als Informationsentropie nach Claude Shannon auch ein Mass für Information.  Die zugehörige Masseinheit ist das Bit. Trotz seiner enormen Bedeutung in der Physik, der Informationstheorie, aber auch im Alltag, gilt der Begriff der Entropie als nerdig und kaum verständlich. Das wäre nicht nötig.

Fünf weit verbreitete Vorurteile erschweren das Verständnis dieses wichtigen Begriffs in der Physik und im Alltag:

Die Entropie spielt auch eine Rolle beim Unterschied zwischen Bits und Distinction nach Spencer-Brown:

Informationsreduktion

Mit der Entropie eng verbunden ist das Phänomen der Informationsreduktion.

Logische Systeme sind immer Vereinfachungen der viel komplexeren und detailhaltigeren Realität. Um zu verstehen, wie wir denken, müssen wir uns mit dieser notgeborenen und unausweichlichen Beschränkung unseres Wissens um die Realität abfinden. Zu diesem natürlichen Vorgang der Informationsreduktion habe ich ab 2019 eine kleine Beitragsserie geschrieben:

Das Thema der Informationsreduktion irritiert viele,  doch wir befinden uns damit auf den Spuren von zwei der wichtigsten europäischen Philosophen, nämlich von William Ockham (Ockhams Razor) und Sokrates (Ich weiss, dass ich nichts weiss).

Entropie wird in Bits gemessen und ist eine der Grundlagen von Information -> Übersichtsseite Informationstheorie

 

Information

Das Bit – Grundbaustein der Information?

Das Bit

Das Bit gilt als Grundbaustein der Information. Doch welche Information trägt dieser Grundbaustein?

Das Bit wurde 1948 von C. E. Shannon zur Berechnung des Informationsflusses in Telefondrähten eingeführt. Es ist die Masseinheit der Informationsentropie.

–> Entropie

Ein alternativer Grundbaustein für Information ist die Unterscheidung (Distinction) nach Georg Spencer-Brown.

Beide Formen, Bit und Unterscheidung, sind so radikal einfach gebaut, dass es einfacher nicht mehr geht. Trotzdem sind sie verschieden. Man kann die beiden Basisformen als komplementär bezeichnen.

 

Information

Entropie zwischen Mikro- und Makroebene

Hinterlassen Sie einen Kommentar

Die zwei Ebenen der Entropie: Mikro und Makro

Zwei Ebenen definieren die Entropie

Die schulmässige physikalische Definition der Entropie weist diese als eine Differenz zwischen zwei Ebenen aus: einer Detail- und einer Übersichtsebene.

Beispiel Kaffeetasse

Klassisch ist die thermale Entropie nach Boltzmann, am Beispiel eines idealen Gases. Die Temperatur (1 Wert) ist direkt verbunden mit den Bewegungsenergien der einzelnen Gasmoleküle (1023 Werte). Mit gewissen Anpassungen gilt das für jedes materielle Objekt, z.B. auch für eine Kaffeetasse:

  1. Thermischer Makrozustand: Temperatur der Flüssigkeit in der Tasse.
  2. Thermischer Mikrozustand: Bewegungsenergie aller einzelnen Moleküle in der Tasse

Die Werte von a) und b) sind direkt verbunden. Die Wärmeengergie der Flüssigkeit, die sich in der Temperatur des Kaffees äussert, setzt sich zusammen aus den Bewegungsenergien der vielen (~ 1023) einzelnen Moleküle in der Flüssigkeit. Je schneller sich die Moleküle bewegen, umso heisser ist der Kaffee.

Die Bewegung der einzelnen Moleküle b) ist jedoch nicht konstant. Vielmehr stossen sich die Moleküle andauernd und ändern dabei ihre Geschwindigkeit und damit auch ihre Energie. Trotzdem ist die Gesamtenergie nach jedem Stoss die gleiche. Wegen dem Energiesatz ändert sich bei jedem Stoss zwar die Energie der beteiligten Moleküle, die Energie aller beteiligten Moleküle zusammen bleibt aber erhalten. Auch wenn der Kaffee langsam abkühlt, oder wenn die Flüssigkeit von aussen erhitzt wird, bleibt der Zusammenhang erhalten: Der einzelne Übersichtswert (Temperatur) und die vielen Detailwerte (Bewegungen) hängen immer gegenseitig voneinander ab.

Beispiel Wald und Bäume

Das bekannte Sprichwort warnt, vor lauter Bäumen den Wald nicht mehr zu sehen.

Wald: Makroebene

Wald: Mikroebene

Auf der Mikroebene sehen wir die Details, auf der Makroebene erkennen wir das grosse Ganze.

Welche Sicht ist nun besser? Die auf den Wald oder auf die Bäume?

  • Sowohl Makroebene wie Mikroebene sind sinnvoll – je nach Aufgabe
  • Beides bezieht sich auf das gleiche Objekt.

Beides ist nicht im gleichen Moment zu sehen:

  • Sieht man die Bäume, verpasst man den Wald
  • Erkennt man den Wald, sieht man nicht alle einzelnen Bäume

Generell glauben wir, dass es besser sei, alle Details zu kennen. Doch das ist eine Täuschung. Wir brauchen immer wieder die Übersicht. Und wir würden uns verlieren in den Details.

Wo ist nun die Entropie?

Wir können nun alle Details der Mikrosicht aufzählen und erhalten so den Informationsgehalt – z.B. in Bits – des Mikrozustandes. Von diesem können wir den viel kleineren Informationsgehalt der Makrosicht abzählen. Die Differenz, die wir erhalten ist die Entropie, nämlich die Information, die im Mikrozustand (Bäume) vorhanden ist, im Makrozustand (Wald) aber fehlt. Die Differenz ist die Entropie.

Warum ist nicht der Informationsgehalt auf der Mikroebene die absolute Entropie?

Der Informationsgehalt auf der Mikroebene lässt sich in Bits berechnen. Entspricht diese Bitmenge der Entropie? Dann wäre der Informationsgehalt auf der Makroebene einfach eine Reduktion der Information. Die eigentliche Information würde dann in der Mikroebene der Details stecken.

Das ist die spontane Erwartung, die ich bei Gesprächspartnern immer wieder antreffe. Sie nehmen an, dass es einen absoluten Informationsgehalt gibt, und der ist in ihren Augen selbstverständlich derjenige mit der grössten Menge an Details.

Das Problem dabei ist: Ds ‹tiefste› Mikrolevel ist gar nicht eindeutig definiert. Die Bäume sind bezogen auf den Wald das tiefere Informationslevel – doch damit ist nicht die tiefste Detailebene erreicht. Man kann die Bäume auf ihre Bestandteile hin – Aste, Zweige, Blätter, Würzeln, Stamm, Zellen usw. – beschreiben, was zweifellos ein tieferes Level ist und noch mehr Details enthalten würde. Doch auch dieses Level wäre nicht tief genug. Wir können durchaus noch tiefer in die Details gehen, und die verschiedenen Zellen des Baumes beschreiben, die Organellen in den Zellen, die Moleküle in den Organellen usw. Wir würden dann weiter bei der Quantenebene ankommen. Doch ist das die tiefste? Vielleicht, doch sicher ist das nicht. Und je weiter wir in die Details gehen, umso mehr entfernen wir uns von der Beschreibung des Waldes. Was uns interessiert ist die Beschreibung des Waldes und dafür ist das tiefste Level gar nicht nötig. Wir tiefer unten wir es suchen, umso mehr entfernen wir uns von der Beschreibung unseres Objekts.

→ Die Tiefe des Mikrolevels ist nicht eindeutig definiert !

Wir können deshalb für unsere Betrachtung nicht von einer eindeutigen absoluten Entropie eines bestimmten Objekts ausgehen. Weil das Mikrolevel beliebig tief ansetzbar ist, ändert sich auch die Entropie, d.h. der quantitative Informationsgehalt auf dieser Ebene. Je tiefer, umso mehr Information, umso höher die Entropie.

Gibt es ein absolutes Makrolevel?

Wie das Mikrolevel ist auch das höchste Informationslevel, z.B. eines Waldes, nicht eindeutig definiert.

Ist dieses Makrolevel das Bild, das eine optische Sicht auf den Wald darstellt, wie es ein über ihm fliegender Vogel sieht? Oder ist des die Darstellung des Waldes auf einer Landkarte? In welchem Masstab? 1:25’000 oder 1:100’000? Offensichtlich ändert sich je nach Sicht die Informationsmenge des jeweiligen Makrozustandes.

Was interessiert uns, wenn wir den Wald beschreiben? Die Wege durch den Wald? Die Baumarten? Hat es Rehe und Hasen? Wie gesund ist der Wald?

Mit anderen Worten: Der Wald kann wie jedes Objekt auf sehr unterschiedlichen Weise beschrieben werden.

Es gibt kein eindeutiges, absolutes Makrolevel. Je nach Situation und Bedürfnissen gilt eine andere Makrodarstellung.

Die Relativität von Mikro- und Makroebene

Auf jeder Ebene gibt es eine jeweilige quantitative Menge an Information, je tiefer umso reichhaltiger, je höher, umso übersichtlicher. Doch es wäre ein Irrtum, eine bestimmte Ebene mit ihrer Informationsmenge als die tiefste oder die höchste zu bezeichnen. Beides ist willkürlich.

Die Information ist die Differenz

Sobald wir akzeptieren, dass sowohl das Mikro- wie das Makrolevel in beliebiger Höhe angesetzt werden können, nähern wir uns einem realeren Informationsbegriff. Es macht plötzlich Sinn, von einer Differenz zu sprechen. Die Differenz zwischen den – jeweils gewählten! – beiden Ebenen definieren die Spanne des Wissens.

Die Information, die ich gewinnen kann, ist die Information, die mir im noch Makrolevel fehlt, die ich aber im Mikrolevel finde. Die Differenz zwischen den beiden Ebenen bezüglich ihrer Entropie ist die Information, die ich dabei gewinnen kann.

Umgekehrt, wenn ich die Details der Mikroebene vor mir habe und eine Übersicht gewinnen will, muss ich diese Information der Mikroebene vereinfachen, und ich muss ihre Bitzahl reduzieren. Diese Reduktion ist die Entropie, d.h. die Information, die auf die ich bewusst verzichte.

Das Informationsparadox

Wenn ich aus einem Wust von Details die Information herausholen will, die mich interessiert, wenn ich also von der Detailbeschreibung zur verwertbaren Information gelangen will, dann muss ich ganz viel Informationen der Mikroebene unter den Tisch fallen lassen. Ich muss Information verlieren, um meine gewünschte Information zu erhalten. Dieses Paradox liegt jedem Analysevorgang zugrunde.

Information ist relativ und dynamisch

Was ich vorschlage ist ein relativer Informationsbegriff. Das entspricht nicht der Erwartung der meisten Mitmenschen, die eine statische Vorstellung von der Welt haben. Die Welt ist aber grundlegend dynamisch. Wir bewegen uns in dieser Welt wie alle anderen Lebewesen als informationsverarbeitende Existenzen. Die Verarbeitung von Information ist ein alltäglicher Vorgang für alle von uns, für alle biologischen Existenzen, ob Pflanzen, Tiere oder Menschen.

Die Verarbeitung von Information ist für alle Lebewesen ein existentieller Prozess. Dieser Prozess hat stets ein Vorher und ein Nachher. Je nachdem gewinnen wir Information, wenn wir etwas im Detail näher ansehen. Und wenn wir eine Übersicht gewinnen wollen, oder einen Entschluss (!) fassen, dann müssen wir Information vereinfachen. Wir gehen also von einer Makrobeschreibung zu einer Mikrobeschreibung und umgekehrt. Information ist dabei eine dynamische Grösse.

Entropie ist die Information, die im Makrolevel fehlt, im Mikrolevel aber zu finden ist.

Und umgekehrt: Entropie ist die Information, die im Mikrolevel vorhanden ist, im Makrolevel – also zur Gewinnung einer Übersicht – ignoriert wird.

Objekte und ihr Mikro- und Makrolevel

Wir können davon ausgehen, dass ein bestimmtes Objekt auf verschiedenen Stufen beschrieben werden kann. Ob eine tiefste Beschreibungsebene zu finden ist, ist gemäss aktuellen naturwissenschaftlichen Erkenntnissen ungewiss, doch für unsere informationstheoretischen Überlegungen letztlich irrelevant. Genauso ist es nicht sinnvoll von einer höchsten Makroebene zu sprechen. Die Makroebenen richten sich nach der Aufgabe der jeweiligen Betrachtung.

Was aber relevant ist, ist der Abstand, also die Information, die im Makrozustand zu gewinnen ist, wenn tiefere Details in die Sicht integriert werden, oder wenn sie – zwecks besserer Übersicht – verworfen werden. Beidemale geht es um eine Differenz zwischen zwei Beschreibungsebenen.

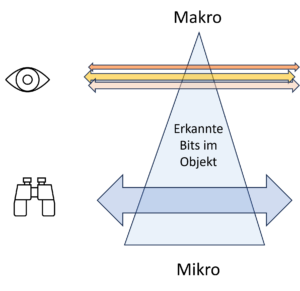
Die Darstellung oben visualisiert die Menge der erkannten Bits in einem Objekt. Oben bei der Makrospitze sind es wenige, unten im Mikrolevel sind es viele. Das Objekt bleibt das gleiche, ob nun viele oder wenige Details berücksichtigt, bzw. erkannt werden.

Die Makrosicht bringt wenige Bits, doch ihre Auswahl wird nicht vom Objekt allein bestimmt, es kommt vielmehr auch auf das Interesse hinter der Sichtweise an.

Die Zahl der Bits, d.h. die Entropie nimmt von unten nach oben ab. Das ist aber nicht eine Eigenschaft des Objekts der Betrachtung, sondern eine Eigenschaft der Betrachtung selber. Je nachdem sehe ich das Objekt anders, einmal detailliert und unübersichtlich, ein anderes Mal übersichtlich und vereinfacht, d.h.einmal mit viel und ein anderes Mal mit weniger Entropie.

Die Informationsgewinnung ist der dynamische Vorgang, der entweder
a) mehr Details erkennt: Makro → Mikro
b) mehr Übersicht gewinnt: Mikro → Makro

Beidemale wird die Informationsmenge (Entropie als Bitmenge) verändert. Die gewonnenen oder verlorenen Bits entsprechen der Differenz der Entropie von Mikro- und Makrolevel.

Wenn ich das Objekt in den Blick nehme, enthüllt es je nach Betrachtungsweise mehr oder weniger Information. Information ist dabei stets relativ zum Vorwissen und dynamisch zu verstehen.

Das ist ein Beitrag zum Thema Entropie. Siehe -> Übersichtsseite Entropie

 

Information

Entropie und Information

Hinterlassen Sie einen Kommentar

Entropie und Information

Der Begriff Entropie wird gerne vermieden, weil er eine gewisse Komplexität enthält, die sich nicht wegdiskutieren lässt.
Doch wenn wir über Information sprechen, müssen wir auch über Entropie sprechen. Denn Entropie ist das Mass für die Informationsmenge. Wir können nicht verstehen, was Information ist, ohne zu verstehen, was Entropie ist.

Information ist immer relativ.

Wir glauben, dass wir Information packen können, so wie wir Bits in einem Speichermedium ablegen. Die Bits sind dann die Information, die objektiv verfügbar ist. Wir haben uns so sehr an dieses Bild gewöhnt, dass wir glauben, dass Information in kleinen Kügelchen daherkommt, die ja und nein sagen können. Doch dieses Bild täuscht.

Denn natürlich sagen die Kügelchen nicht ‹ja› oder ’nein›, nicht 0 oder 1, nicht TRUE oder FALSE, und auch sonst nichts bestimmtes. Bits haben gar keine Bedeutung, es sei denn, man habe diese Bedeutung von aussen her definiert. Dann können sie sehr gut 1, TRUE, ‹Ich komme heute zum Abendessen› oder irgend etwas anderes aussagen, jedoch erst zusammen mit ihrer Umgebung, ihrem Kontext.

Aus dieser Überlegung wird klar, dass Information relativ ist. Das Bit bekommt seine Bedeutung erst aus einer bestimmten Einordnung heraus. Je nachdem bedeutet es 0 oder 1, ‹Wahr› oder ‹Falsch›, usw. Das Bit ist an seinem Platz zwar gesetzt, doch seine Bedeutung bekommt es erst durch seinen Platz.
Somit muss der Platz, also der Kontext mit hineingenommen werden, damit klar wird, was das Bit bedeuten soll. Und natürlich ist die Bedeutung relativ, das heisst, das gleiche Bit, kann in einem anderen Kontext, einem anderen Platz eine ganz andere Bedeutung haben.

Diese Relativität ist nun charakteristisch nicht nur für das Bit, sondern für jede Art Information. Jede Information bekommt ihre Bedeutung erst durch den Kontext, in dem sie steht. Sie ist also relativ. Denken Sie das am besten an Beispielen aus Ihrem Leben durch. Information ist nicht das Signal, das auf ‹ja› oder ’nein› steht. Dieses Signal ist nur das Signal. Was es bedeutet, wird erst klar, wenn Sie das Signal aus Ihrer Warte heraus interpretieren, wenn Sie es aus Ihrem Kontext heraus ansehen.
Erst dann bekommt das Signal für Sie eine Bedeutung. Diese Bedeutung liegt nicht absolut, d.h. isolierbar im Signal Bit, sondern relativ in der Interaktion zwischen Ihrer Erwartung , dem Kontext, und der Stellung des Schalters, der auf ON oder OFF gestellt sein kann. Dieser Schalter ist das Bit. Seine Bedeutung an sich, also wenn das Bit isoliert wird, ist nur ON oder OFF.
Alles andere liegt in der Umgebung.

Definition der Entropie

In Anbetracht der Tatsache, wie wichtig Information und Informationstechnologien sind, ist es schon erstaunlich, wie wenig bekannt die wissenschaftliche Defintion von Entropie, also von Information ist:

Entropie ist das Mass für die Information, die im Mikrozustand bekannt ist, im Makrozustand aber nicht.

Die Entropie hängt somit eng mit der Information auf Mikro- und Makrolevel zusammen, und sie kann als ‹Abstand› oder Differenz der Information auf den beiden Informationsebenen gesehen werden.

Mikro- und Makroebene

Was ist mit diesem Abstand zwischen Mikro- und Makroebene gemeint? – Die Mikroebene enthält die Details (also viel Information), die Makroebene die Übersicht (also weniger, dafür gezieltere Information). Der Abstand zwischen den beiden Ebenen kann sehr klein sein (wie beim Bit, wo das Mikrolevel gerade zwei Informationen kennt: on oder off ) oder aber riesig gross, wie z.B. bei der Temperatur (Makrolevel)  des Kaffees, wo Bewegungsenergien der vielen Moleküle (Mikrolevel) die Temperatur des Kaffees bestimmt. Die Zahl der Moleküle liegt in diesem Fall in der Grössenordnung der Avogadroschen Zahl 1023, also ganz schön hoch, und die Entropie des Kaffees in der Tasse ist entsprechend wirklich sehr hoch.

Andererseits gibt es auch ‹kleine› Informationen, die sehr nahe an der Grössenordnung eines Bits (Infogehalt = 1) heran kommen. Immer aber kommt es auf das Verhältnis von Mikro- zu Makrozustand an. Dieses Verhältnis – also was im Mikrozustand gewusst wird, im Makrozustand aber nicht – definiert die Information.

Die Komplexität des Makrozustandes

Der Makrozustand enthält stets weniger Information als der Mikrozustand, er ist eine gezielte Vereinfachung der Information des Mikrozustandes.

For example: a certain individual (micro level), can belong to the collective macro groups of Swiss inhabitants, computer scientists, older men, contemporaries of the year 2024, etc., all at the same time.

Das führt dazu, dass der gleiche Mikrozustand verschiedene Makrozustände beliefern kann. Zum Beispiel: Ein Individuum des Mikrolevels kann in der komplexen Welt der Gesellschaft mehreren Makrogruppen angehören, also gleichzeitig den Makrogruppen der Schweizer, der Informatiker, der älteren Männer, der Zeitgenossen des Jahres 2024 usw. Alle diese Makrogruppen bestehen aus vielen Individuen und sie überschneiden und durchdringen sich auf wechselnde Weise.

Die Möglichkeit, aus verschiedenen Mikrozuständen gleichzeitig mehrere Makrozustände herauszuziehen, ist charakteristisch für die Komplexität von Mikro- und Makrozustand und somit auch für die Entropie.

So einfach lässt sich also die Entropieüberlegung nicht in komplexere Netze übertragen, wie es die einfachen Beispiele der Kaffeetasse nach Boltzmann, des verlorene Schlüssel nach Salm oder das simple Bit vermuten lassen.

Siehe auch:
– Paradoxe Logikkerne, Teil 2
– Bit und Unterscheidung
– Fünf Vorurteile über Entropie

Das ist ein Beitrag zum Thema Entropie. Siehe -> Übersichtsseite Entropie

 

Information, Logik

Das Bit hat keine Bedeutung

Hinterlassen Sie einen Kommentar

Das Bit ist die Basis der IT

Unsere Informationstechnologie baut auf dem Bit auf. Alles, was in unseren Computern geschieht, basiert auf diesem kleinsten Basiselement der Information. Wenn Sie gefragt werden, was ein einzelnes Bit bedeutet, werden Sie möglicherweise antworten, dass das Bit zwei Zustände einnehmen kann, von denen der eine 0 ist und der andere 1 bedeutet. Auf diese Weise können wir bekanntlich beliebig hohe Zahlen schreiben, wir müssen einfach genügend Bits hintereinander reihen.

Aber stimmt das auch? Bedeutet wirklich der eine Zustand im Bit 0 und der andere 1? Können die beiden Zustände nicht auch ganz andere Bedeutungen annehmen?

Dem Bit können beliebige Bedeutungen zugeschrieben werden

In der Tat können die beiden Zustände des Bits irgendeine Bedeutung einnehmen. Beliebt sind neben 0/1 auch Wahr/Falsch, Ja/Nein, Positiv/Negativ, aber im Prinzip und in der Praxis können dem Bit von aussen irgendwelche Bedeutungen zugeschrieben werden. Selbstverständlich sind auch Umkehrungen erlaubt, also neben 0/1 auch 1/0.

Die Zuschreibung der Bedeutung des Bits erfolgt von aussen

Ob das konkrete Bit im Computerprogramm nun 0/1 oder 1/0 oder irgendetwas anderes bedeutet, spielt selbstverständlich eine entscheidende Rolle. Die Bedeutung liegt aber nicht im Bit selber, denn das Bit ist eine höchst radikale Abstraktion. Es sagt nur aus, dass zwei Zustände existieren und welcher zur Laufzeit gerade aktuell ist. Was die beiden aber bedeuten, ist eine ganz andere Geschichte, die über das einzelne Bit weit hinausgeht. In einem Computerprogramm kann z.B. deklariert werden, dass das Bit dem Wertepaar TRUE/FALSE entspricht. Das gleiche Bit kann aber auch mit anderen Bits zusammen als Teil einer Zahl oder eines Buchstabencodes interpretiert werden – sehr unterschiedliche Bedeutungen also, je nach Programmkontext.

Digitaler und analoger Kontext

Das Softwareprogramm ist der digitale Kontext und er besteht selbstverständlich aus weiteren Bits. Diese Bits aus der Umgebung können verwendet werden, um die Bedeutung eines Bits zu bestimmen. Nehmen wir an, unser Bit sei mit weiteren Bits daran beteiligt, den Buchstaben ‹f› zu definieren. Unser Programm sei auch so organisiert, dass dieser Buchstabe in eine Tabelle zu stehen kommt, und zwar in eine Spalte, die mit ‹Geschlecht› überschrieben ist. All dies ist in der Software klar geregelt. Legt nun die Software die Bedeutung des Bits fest? Sicher sind Sie nicht überrascht, wenn das ‹f› die Bedeutung ‹feminin› hat und die Tabelle vermutlich verschiedene Personen auflistet, die männlich oder weiblich (f) sein können. Was aber bedeuten männlich und weiblich? Erst in der analogen Welt bekommen diese Ausdrücke eine Bedeutung.

Das Bit, die perfekte Abstraktion

Das Bit stellt in der Tat den Endpunkt einer radikalen Informationsabstraktion dar. Die Information ist im einzelnen Bit soweit auf das absolut Elementare reduziert, dass die Information über die Bedeutung aus dem Bit vollständig herausgenommen worden ist. Das Bit sagt nur noch aus, dass zwei – ausserhalb des Bits beschriebene – Zustände existieren und welcher der beiden zu einem bestimmten Zeitpunkt aktuell ist.

Diese radikale Abstraktion ist gewollt und in einer Software sehr sinnvoll. Denn so kann das gleiche physische Bit im Chip des Computer immer wieder neu verwendet werden, einmal als TRUE/FALSE-Paar, einmal als 0/1, einmal als JA/NEIN usw. Das ist sehr praktisch und ermöglicht dem Computer, beliebige Aufgaben zu erfüllen. Die dadurch gewonnene perfekte Abstraktion nimmt dem einzelnen Bit aber gleichzeitig seine individuelle Bedeutung und diese kann und muss dann für jede Anwendung von aussen neu gegeben werden.

Der unendliche Regress

Wenn die Bedeutung des Bits von aussen gegeben wird, dann können natürlich andere Bits diese Aufgabe übernehmen und die Bedeutung des einen Bits definieren. Dazu müssen aber diese äusseren Bits die entsprechende Wirkkraft haben, die natürlich nicht ohne deren eigenen Bedeutung zu haben ist. Und selbstverständlich liegen die Bedeutungen der Bits dieses äusseren Kreises nicht in diesen Bits selber – aus den gleichen Gründen wie oben – sondern sie müssen von aussen, d.h. von einem weiteren Kreis von Bits gegeben werden. Die Bits dieses zweiten äusseren Kreises müssen in einem weiteren Kreis erklärt werden und die Bedeutung der Bits dieses weiteren Kreises wiederum von einem noch äusseren  …  Selbstverständlich kommt dieser Prozess der Bedeutungszuordnung in einer Welt von Bits nie an sein Ende, der Regress ist unendlich.

Erst im Analogen endet der unendliche Regress

Erst wenn wir aus dem Programm in die Realwelt heraustreten, können wir den Informationen aus dem Computer wirkliche eine Bedeutung zuordnen.

Selektiver und deskriptiver Informationsgehalt

Wenn wir das oben Beschriebene rekapitulieren können wir im Bit Folgendes unterscheiden:

Der deskriptive Informationsgehalt sagt aus, was das Bit bedeutet, er beschreibt die beiden Zustände des Bits, sagt aber nicht aus, welcher Zustand aktuell gewählt ist.  Der selektive Informationsgehalt andererseits sagt aus, welcher der beiden Zustände aktuell ist, weiss aber nichts über die Eigenschaften der beiden Zustände, und somit auch nichts über ihre jeweilige Bedeutung.

Die Unterscheidung zwischen selektivem und deskriptivem Informationsgehalt wurden vom britischen Radar-Pionier und Informationswissenschaftler Donald MacKay in den 40-er Jahren des letzten Jahrhunderts geprägt, praktisch gleichzeitig mit der ersten Erwähnung und Beschreibung des klassischen Bits durch den Amerikaner C. A. Shannon. MacKay hat auch bereits sehr klar erkannt, dass das Bit von Shannon nur einen selektiven Informationsgehalt trägt und der deskriptive von aussen gegeben werden muss.

Erstaunlicherweise ist diese Erkenntnis von MacKay heute beinahe in Vergessenheit geraten.

Fazit:

1. Das Bit liefert den selektiven Informationsgehalt.
2. Der deskriptive Informationsgehalt liegt nicht im Bit.
3. Ein isoliertes Bit trägt allein keine Bedeutung.
4. Die Bedeutung des Bits wird stets von ausserhalb des Bits gegeben.
5. Dadurch wird ein unendlicher Regress initiiert.
6. Erst im Analogen endet der unendliche Regress.

Die Zahl der Bits misst die Quantität von Information -> Übersichtsseite Informationstheorie

Information, Logik

Die Unterscheidung (nach Spencer-Brown) und das Bit

Hinterlassen Sie einen Kommentar

Fortsetzung von Paradoxe Logikkerne (2)

Geschichte

Bevor wir die Konsequenzen der Distinction von Georg Spencer-Brown (GSB) auf Logik, Physik, Biologie und Philosophie ansehen, ist es hilfreich, sie mit einer anderen, viel bekannteren Grundform zu vergleichen, nämlich dem Bit. Das ermöglich uns, die Natur von GSB’s distinction und das Revolutionäre seiner Innovation besser zu verstehen.

Bits und Forms können beide als Basis-Bausteine für die Informationsverarbeitung angesehen werden. Software-Strukturen bauen technisch auf Bits auf, doch die Forms von GSB («draw a distinction») sind genauso einfach, grundlegend und dabei verblüffend ähnlich. Trotzdem gibt es charakteristische Unterschiede.

     

Abb. 1: Form und Bit zeigen Ähnlichkeit und Unterschiede

Sowohl Bit wie die Spencer-Brown Form sind in der Frühphase der Informatik entstanden, also relativ neue Vorstellung. Das Bit wurde von C.A. Shannon 1948 beschrieben, die Distinction von Georg Spencer-Brown (GSB) in seinem Buch «Laws of Form» im Jahr 1969, also nur ca. 20 Jahre später. 1969 fiel in die hohe Zeit der Hippie-Bewegung und GSB wurde in der Tat in Kaliforniens Hippie-Hochburg Esalen hoch willkommen geheissen. Das hat möglicherweise ein schlechtes Licht auf ihn geworfen und den etablierten Wissenschaftsbetrieb von ihm abgehalten. Während das Bit Kaliforniens entstehende Informations-High-Tech-Bewegung beflügelte, wurde Spencer-Browns mathematisch-logische Revolution von der Scientific Community geflissentlich ignoriert. Es ist Zeit, diesen Misstand zu überwinden.

Gemeinsamkeiten von Distinction und Bit

Beide, die Form und das Bit, beziehen sich auf Information. Beide sind elementare Abstraktionen und können deshalb als Grundbausteine von Information gesehen werden.

Diese Gemeinsamkeit zeigt sich darin, dass beide einen einzigen Aktionschritt bezeichnen – wenn auch einen unterschiedlichen – und beide dieser Aktion eine maximal reduzierte Anzahl von Ergebnissen zuordnen, nämlich genau zwei.

Tabelle 1: Sowohl Bit wie Distinction beinhalten
je eine Aktion und zwei mögliche Resultate (Outcomes)

Genau eine Aktion, genau zwei potentielle Ergebnisse

Die Aktion der Distinction ist die Distinction, also die Unterscheidung, die Aktion des Bits ist die Auswahl, also die Selection. Beide Aktionen sind als Informationshandlungen zu sehen und als solche fundamental, d.h. nicht weiter reduzierbar. Das Bit enthält in sich nicht weitere Bits, die Distinktion enthält in sich nicht weitere Distinktionen. Natürlich gibt es in der Umgebung des Bits weitere Bits und in der Umgebung einer Distinktion weitere Distinktionen. Beide Aktionen sind aber als fundamentale Informationshandlungen zu sehen. Ihre Fundamentalität wird unterstrichen durch die kleinst mögliche Zahl ihrer Ergebnisse, nämlich zwei. Die Zahl der Ergebnisse kann nicht kleiner sein, denn eine Unterscheidung von 1 ist keine Unterscheidung und eine Selektion aus 1 ist keine Selektion. Beides ist erst möglich, wenn es zwei potentielle Ergebnisse gibt.

Sowohl Distinction wie Bit sind somit unteilbare Informationshandlungen von radikaler, nicht zu steigernder Simplizität.

Trotzdem sind sie nicht gleich und auch nicht austauschbar. Sie ergänzen sich.

Während das Bit seit 1948 einen technischen Höhenflug angetreten ist, ist seine Voraussetzung, die Unterscheidung (distinction), ungenannt im Hintergrund geblieben. Umso mehr lohnt es sich, sie heute in den Vordergrund zu rücken und so ein neues Licht auf die Grundlagen von Mathematik, Logik, Natur- und Geisteswissenschaften zu werfen.

Unterschiede

Informationsgehalt und die Entropie nach Shannon

Beide, Form und Bit, beziehen sich auf Information. In der Physik wird der quantitative Gehalt an Information als Entropie bezeichnet.

Der Informationsgehalt, wenn ein Bit gesetzt, bzw. eine Unterscheidung getroffen wird, ist auf den ersten Blick in beiden Fällen gleich gross, nämlich die Information, die zwischen zwei Zuständen unterscheidet. Das ist beim Bit ganz klar so. Sein Informationsgehalt ist, wie Shannon gezeigt hat, log2(2) = 1. Shannon hat diesen dimensionslosen Wert als 1 Bit bezeichnet. Das Bit enthält somit – nicht ganz überraschend – die Information von einem Bit. So ist es von Shannon definiert worden.

Das Bit und die Entropie

Das Bit misst nichts anderes als die Entropie. Der Begriff Entropie stammt ursprünglich aus der Wärmelehre und dient dazu, das Verhalten von Wärmemaschinen zu berechnen. Entropie ist der Partnerbegriff der Energie und gilt – wie der Begriff Energie – überall in der Physik, nicht nur in der Wärmelehre.

Was ist Entropie?

Die Entropie misst also – seit Shannon – den Informationsgehalt. Wenn ich etwas nicht weiss und es anschliessend erfahre, fliesst Entropie als Information. Wenn – bevor ich weiss, was gilt – zwei Zustände möglich sind, dann erhalte ich, wenn ich erfahre, welcher der beiden Zustände zutrifft, eine Information mit dem quantitativen Wert 1 Bit.

Wenn mehr als zwei Zustände möglich sind, steigt die Zahl der Bits logarithmisch mit der Zahl der möglichen Zustände; so braucht es drei 2-er Wahlen um aus 8 Möglichkeiten die zutreffende herauszufinden, also genau drei Bits. Die Zahl der Wahlen (Bits) verhält sich zur Zahl der Auswahlmöglichkeiten wie das Beispiel zeigt, logarithmisch.

Zweierwahl = 1 Bit = log2(2).
Viererwahl = 2 Bit = log2(4)
Achterwahl = 3 Bit = log2(8)

Der Informationsgehalt eines einzigen Bits ist stets der Informationsgehalt einer einzigen Zweierwahl, also log2(2) = 1. Das Bit als physikalische Grösse ist dimensionslos, also eine reine Zahl. Das passt, weil die Information über die Wahl neutral ist, und nicht etwa eine Länge, ein Gewicht, eine Energie oder eine Temperatur. So viel zum Bit, der technischen Einheit der des quantitativen Informationsgehaltes. Wie verhält es sich nun bei der anderen Grundeinheit von Information, der Form von Spencer-Brown?

Der Informationsgehalt der Form

Der Informationsgehalt des Bits ist genau 1, wenn die beiden Outcomes der Selektion genau gleich wahrscheinlich sind. Sobald von zwei Zuständen einer unwahrscheinlicher ist, ist die Information grösser, wenn er, trotz der geringeren Vorwahrscheinlichkeit, gewählt wird. Je unwahrscheinlicher er ist, umso grösser wird die Information, wenn die Wahl auf ihn fällt. Nur beim klassischen Bit ist die Wahrscheinlichkeit für beide Zustände per Definition gleich gross.

Das ist ganz anders bei der Form der Unterscheidung von Spencer-Brown. Das Entscheidende dabei ist der ‹unmarked space›. Die Distinktion unterscheidet etwas vom Rest und markiert es. Der Rest, also alles andere bleibt unmarkiert, Spencer-Brown nennt es den ‹unmarked space›.

Wir können und müssen nun davon ausgehen, dass der Rest, das Unmarkierte, viel grösser ist, und die Wahrscheinlichkeit seines Eintretens viel grösser ist, als die Wahrscheinlichkeit, dass das Markierte eintrifft. Der Informationsgehalt des Markierten ist deshalb immer grösser als 1.

Natürlich geht es bei der Unterscheidung um das Markierte. Deshalb wird für den Informationsgehalt der Unterscheidung das Markierte und nicht das Unmarkierte gerechnet. Wie gross ist nun der Raum des Unmarkierten? Wir tun gut daran, davon ausgehen, dass er unendlich ist. Ich kann nie wissen, was ich alles nicht weiss.

Der Unterschied im Informationsgehalt, gemessen als Entropie, ist der erste Unterschied zwischen Bit und Unterscheidung. Beim Bit ist der Informationsgehalt, d.h. die Entropie genau 1, bei der Unterscheidung kommt es darauf an, wie gross der Unmarkierte Raum gesehen wird, er ist aber stets grösser als der markierte und die Entropie der Unterscheidung ist deshalb aus mathematischen Gründen stets grösser als 1.

Geschlossenheit und Offenheit

Die Abb. 1 oben zeigt den wichtigsten Unterschied von Distinktion und Bit, nämlich ihre Grenzen gegen aussen. Diese ist beim Bit klar definiert.

Die Bedeutungen im einem Bit

Das Bit enthält zwei Zustände, von denen einer aktiviert ist, der andere nicht. Ausser diesen beiden Zuständen ist nichts im Bit zu sehen und alle andere Information befindet sich ausserhalb des Bits. Nicht einmal die Bedeutungen der beiden Zustände sind definiert. Sie können 0 und 1, Wahr undd Falsch, Positiv und Negativ oder jedes andere Paar bedeuten, das sich gegenseitig ausschliesst. Das Bit selber enthält diese Bedeutungen nicht, nur die Information, welcher der beiden Zustände gewählt wurde. Die Bedeutung der beiden Zuständen wird ausserhalb des Bits geregelt und von ausserhalb zugewiesen. Diese Neutralität des Bits ist seine Stärke. Es kann jede Bedeutung annehmen und ist deshalb überall einsetzbar, wo Information technisch prozessiert wird.

Die Bedeutung in einer Unterscheidung

Ganz anders ist das bei der Unterscheidung. Hier wird die Bedeutung markiert. Dazu wird das Innere der Unterscheidung vom Äusseren unterschieden. Das Äussere aber ist offen und es gibt nichts, was nicht dazu gehört. Der ‹unmarked space› ist im Prinzip unendlich. Eine Grenze wird definiert, doch sie ist die Unterscheidung selber. Deshalb kann sich die Unterscheidung nicht wirklich gegen aussen abgrenzen, im Gegensatz zum Bit.

Mit anderen Worten:

→  Das Bit ist geschlossen, die Unterscheidung nicht.

Unterschiede zwischen Unterscheidung und Bit


Tabelle 2: Unterschiede ziwschen Distinction (Form) und Bit

Die Unterschiede haben nun einige interessante Konsequenzen.

Konsequenzen

Bits und Offenheit in einer Software (Beispiel NLP)

Das Bit hat durch seine definierte und simple Entropie den technologischen Vorteil der einfachen Handhabbarkeit, was wir uns in der Software-Industrie zu Nutze machen. Die Forms hingegen sind durch ihre Offenheit realitätsgerechter. Für unsere konkrete Aufgabe der Interpretation von medizinischen Texten stiessen wir deshalb auf die Notwendigket, die Offenheit auch in der Bitwelt der technischen Software durch bestimmte Prinzipien einzuführen. Stichworte dazu sind:

  1. Einführung eines handelnden Subjekts, das den Input nach eigenen Internen Regeln bewertet,
  2. Arbeiten mit wechselnden Ontologien und Klassifikationen,
  3. Abkehr von der klassischen, d.h. statischen und monotonen Logik zu einer nicht-monotonen Logik,
  4. Integration der Zeit als Logikelement (nicht nur als Variable).

Mehr zum Thema Information -> Übersichtsseite Informationstheorie

 

Information, Semantik

Das Bit hat keine Bedeutung

Hinterlassen Sie einen Kommentar

Das Bit ist die Basis der IT

Unsere Informationstechnologie baut auf dem Bit auf. Alles, was in unseren Computern geschieht, basiert auf diesem kleinsten Basiselement der Information. Wenn Sie gefragt werden, was ein einzelnes Bit bedeutet, werden Sie möglicherweise antworten, dass das Bit zwei Zustände einnehmen kann, von denen der eine 0 ist und der andere 1 bedeutet. Auf diese Weise können wir bekanntlich beliebig hohe Zahlen schreiben, wir müssen einfach genügend Bits hintereinander reihen.

Aber stimmt das auch? Bedeutet wirklich der eine Zustand im Bit 0 und der andere 1? Können die beiden Zustände nicht auch ganz andere Bedeutungen annehmen?

Dem Bit können beliebige Bedeutungen zugeschrieben werden

In der Tat können die beiden Zustände des Bits irgendeine Bedeutung einnehmen. Beliebt sind neben 0/1 auch Wahr/Falsch, Ja/Nein, Positiv/Negativ, aber im Prinzip und in der Praxis können dem Bit von aussen irgendwelche Bedeutungen zugeschrieben werden. Selbstverständlich sind auch Umkehrungen erlaubt, also neben 0/1 auch 1/0.

Die Zuschreibung der Bedeutung des Bits erfolgt von aussen

Ob das konkrete Bit im Computerprogramm nun 0/1 oder 1/0 oder irgendetwas anderes bedeutet, spielt selbstverständlich eine entscheidende Rolle. Die Bedeutung liegt aber nicht im Bit selber, denn das Bit ist eine höchst radikale Abstraktion. Es sagt nur aus, dass zwei Zustände existieren und welcher zur Laufzeit gerade aktuell ist. Was die beiden aber bedeuten, ist eine ganz andere Geschichte, die über das einzelne Bit weit hinausgeht. In einem Computerprogramm kann z.B. deklariert werden, dass das Bit dem Wertepaar TRUE/FALSE entspricht. Das gleiche Bit kann aber auch mit anderen Bits zusammen als Teil einer Zahl oder eines Buchstabencodes interpretiert werden – sehr unterschiedliche Bedeutungen also, je nach Programmkontext.

Digitaler und analoger Kontext

Das Softwareprogramm ist der digitale Kontext und er besteht selbstverständlich aus weiteren Bits. Diese Bits aus der Umgebung können verwendet werden, um die Bedeutung eines Bits zu bestimmen. Nehmen wir an, unser Bit sei mit weiteren Bits daran beteiligt, den Buchstaben ‹f› zu definieren. Unser Programm sei auch so organisiert, dass dieser Buchstabe in eine Tabelle zu stehen kommt, und zwar in eine Spalte, die mit ‹Geschlecht› überschrieben ist. All dies ist in der Software klar geregelt. Legt nun die Software die Bedeutung des Bits fest? Sicher sind Sie nicht überrascht, wenn das ‹f› die Bedeutung ‹feminin› hat und die Tabelle vermutlich verschiedene Personen auflistet, die männlich oder weiblich (f) sein können. Was aber bedeuten männlich und weiblich? Erst in der analogen Welt bekommen diese Ausdrücke eine Bedeutung.

Das Bit, die perfekte Abstraktion

Das Bit stellt in der Tat den Endpunkt einer radikalen Informationsabstraktion dar. Die Information ist im einzelnen Bit soweit auf das absolut Elementare reduziert, dass die Information über die Bedeutung aus dem Bit vollständig herausgenommen worden ist. Das Bit sagt nur noch aus, dass zwei – ausserhalb des Bits beschriebene – Zustände existieren und welcher der beiden zu einem bestimmten Zeitpunkt aktuell ist.

Diese radikale Abstraktion ist gewollt und in einer Software sehr sinnvoll. Denn so kann das gleiche physische Bit im Chip des Computer immer wieder neu verwendet werden, einmal als TRUE/FALSE-Paar, einmal als 0/1, einmal als JA/NEIN usw. Das ist sehr praktisch und ermöglicht dem Computer, beliebige Aufgaben zu erfüllen. Die dadurch gewonnene perfekte Abstraktion nimmt dem einzelnen Bit aber gleichzeitig seine individuelle Bedeutung und diese kann und muss dann für jede Anwendung von aussen neu gegeben werden.

Der unendliche Regress

Wenn die Bedeutung des Bits von aussen gegeben wird, dann können natürlich andere Bits diese Aufgabe übernehmen und die Bedeutung des einen Bits definieren. Dazu müssen aber diese äusseren Bits die entsprechende Wirkkraft haben, die natürlich nicht ohne deren eigenen Bedeutung zu haben ist. Und selbstverständlich liegen die Bedeutungen der Bits dieses äusseren Kreises nicht in diesen Bits selber – aus den gleichen Gründen wie oben – sondern sie müssen von aussen, d.h. von einem weiteren Kreis von Bits gegeben werden. Die Bits dieses zweiten äusseren Kreises müssen in einem weiteren Kreis erklärt werden und die Bedeutung der Bits dieses weiteren Kreises wiederum von einem noch äusseren  …  Selbstverständlich kommt dieser Prozess der Bedeutungszuordnung in einer Welt von Bits nie an sein Ende, der Regress ist unendlich.

Erst im Analogen endet der unendliche Regress

Erst wenn wir aus dem Programm in die Realwelt heraustreten, können wir den Informationen aus dem Computer wirkliche eine Bedeutung zuordnen.

Selektiver und deskriptiver Informationsgehalt

Wenn wir das oben Beschriebene rekapitulieren können wir im Bit Folgendes unterscheiden:

Der deskriptive Informationsgehalt sagt aus, was das Bit bedeutet, er beschreibt die beiden Zustände des Bits, sagt aber nicht aus, welcher Zustand aktuell gewählt ist.  Der selektive Informationsgehalt andererseits sagt aus, welcher der beiden Zustände aktuell ist, weiss aber nichts über die Eigenschaften der beiden Zustände, und somit auch nichts über ihre jeweilige Bedeutung.

Die Unterscheidung zwischen selektivem und deskriptivem Informationsgehalt wurden vom britischen Radar-Pionier und Informationswissenschaftler Donald McKay in den 40-er Jahren des letzten Jahrhunderts geprägt, praktisch gleichzeitig mit der ersten Erwähnung und Beschreibung des klassischen Bits durch den Amerikaner Shannon. McKay hat auch bereits sehr klar erkannt, dass das Bit von Shannon nur einen selektiven Informationsgehalt trägt und der deskriptive muss von aussen gegeben werden.

Erstaunlicherweise ist diese Erkenntnis von McKay heute beinahe in Vergessenheit geraten.

Fazit:

1. Das Bit liefert den selektiven Informationsgehalt.
2. Der deskriptive Informationsgehalt liegt nicht im Bit.
3. Das Bit hat allein somit auch keine Bedeutung.
4. Die Bedeutung des Bits wird stets von aussen gegeben.
5. Dadurch wird ein unendlicher Regress initiiert.
6. Erst im Analogen endet der unendliche Regress.

Mehr zum Thema Information -> Übersichtsseite Informationstheorie

 

Information

Welche Information trägt ein Bit?

Hinterlassen Sie einen Kommentar

Die Frage erscheint Ihnen vermutlich banal. Schliesslich weiss jedermann, was ein Bit ist, nämlich die Möglichkeit einmal aus zwei Zuständen auszuwählen.

Wo ist das Problem?

Ich möchte zu bedenken geben, dass die Frage nach der Information im Bit damit noch nicht beantwortet ist. Welche Information in einem Bit enthalten ist, hat nämlich auch mit der Frage zu tun, welche zwei Zustände überhaupt zur Auswahl stehen. Klassische Beispiele sind:

– 0 und 1
– Wahr und Falsch
– Positiv und Negativ
– Ein und Aus

Selbstverständlich erschöpft sich die Auswahl dadurch nicht. Auch männlich/weiblich, innen/aussen, gut/schlecht oder beliebige andere binäre Paare können in einem Bit stecken, genauso wie ihre jeweiligen Umkehrungen, also neben 0/1 genauso auch 1/0.

Woher weiss das Bit, welche beiden Zustände es anbietet?

Vielleicht denken Sie, dass dies einfach eine Sache im Bit sei. Das eine Bit enthält 0/1 als Paar und das andere Bit Wahr/Falsch. Die beiden Zustände wären somit natürliche Eigenschaften der jeweiligen individuellen Bits. Das trifft jedoch nicht zu, denn der Hersteller eines Chips hat die Bits des Chips nicht mit individuellen Eigenschaften versehen. Technisch gesehen sind die Bits alle genau gleich, ihre Simplizität und Neutralität macht ja gerade den Charme der binären Technologien aus.

Erst wenn im Computer ein Programm abläuft, werden den neutralen Bits individuelle Wertpaare wie 0/1, Wahr/Falsch usw. zugeordnet. Der Charakter, d.h. die eigentliche Bedeutung der beiden Zustände, wird erst durch das Programm in das Bit hineingelegt.

Das ist natürlich praktisch, weil so je nach Programm dem gleichen Bit im Chip eine immer wieder neue Bedeutung gegeben werden kann. Allerdings müssen wir jetzt zugeben, dass die Bedeutung nicht mehr im Bit steckt, sondern im aufrufenden Programm, mithin in ganz anderen Bits, nämlich denen des Programms.

Woher aber haben diese Bits wiederum ihre Bedeutung? Bei denen verhält es sich natürlich genau gleich, auch ihnen werden erst von aussen konkrete Wertepaare zugeordnet. Es geht also immer weiter nach aussen, und immer kann die Bedeutung des Wertepaares eines Bits nur mit weiteren Bits von aussen geschrieben werden – mit anderen Worten: Es handelt sich einen unendlichen Regress, jedes Bit, das ein anderes erklärt, muss erneut erklärt werden.

Wo ist das Ende der Kette?

Die Suche nach den Bits, mit denen man die anderen Bits erklären kann, findet somit nie ein Ende. Das ist die Natur eines unendlichen Regresses. Doch wir haben trotzdem eine Chance, das Ende des Regresses zu finden. Die Suche ist nämlich nur solange hoffnungslos, wie wir innerhalb des Computers bleiben. Als Mensch jedoch können Sie über den Computer hinausdenken. Das Programm ist ja zu einem bestimmten Zweck geschrieben worden und Menschen, Programmierer und Anwender, legen fest, welche Bedeutungen die Bits jeweils haben sollen. Die Bedeutung, und damit die konkreten individuellen Wertpaare der Bits entstehen am Ende des Regresses – offline – als Abmachung in den Köpfen der Menschen.

Allerdings sind wir auf diese Weise aus der Welt der Bits herausgerutscht, und meine Behauptung ist, dass es anders nicht geht. Solange wir in der Welt der Bits bleiben, bleiben wir in einer zwar präzisen, doch völlig „unbedeutenden“ Welt. Diese erlangt ihre Bedeutung erst, wenn wir den einzelnen Bits von aussen eine Bedeutung geben. Das heisst, wir verbinden ein bestimmtes Bit mit einer Information, die uns als Menschen etwas sagt. So lässt sich der unendliche Regress auflösen.

Isoliert gesehen, sind die beiden Zustände des Bits vollständig neutral und lassen sich deshalb mit beliebigen Bedeutungen belegen. Technisch gesehen ist das genial. Doch dürfen wir uns dadurch nicht verleiten lassen, mit Bits allein bedeutungstragende Information generieren zu können. Es braucht immer ein Aussen, das den Bits die Bedeutung zuweist.

Wir haben somit zwei Arten von Information:

A) Das isolierte Bit:
Dieses sagt aus, welcher der beiden Zustände des Bits gewählt wird, ohne die Zustände selber zu beschreiben. Es handelt sich um das technische Bit der konventionellen Informationstheorie.

B) Die dem Bit zugedachte Bedeutung:
Diese Information sagt aus, worum es beim Bit geht, welche beiden Zustände es sind, die mit dem Bit gewählt werden können. Es handelt sich um die qualitative Information, die mit dem Bit ausgedrückt werden kann. Obwohl wir sie dem Bit selber zuordnen, verschwindet sie, sobald wir das Bit isoliert betrachten.

Die beiden Arten von Information sind von prinzipiell unterschiedlicher Natur. Trotz oder gerade wegen ihrer unterschiedlichen Natur gehören sie zusammen. Erst ihre Kombination macht eine sinnvolle, das heisst bedeutungstragende Information aus.

Mehr zum Thema Information -> Übersichtsseite Informationstheorie