Dies ist ein Beitrag zur Entstehung der Tonleitern und setzt den Beitrag zur Oktave fort.
Wir erzeugen eine Resonanz
Falls Resonanz für Sie ein abstraktes – oder noch kein erlebtes musikalisches – Phänomen ist, empfehle ich Ihnen folgendes einfaches Experiment: Suchen sie ein Klavier (kein digitales) und auf dem Klavier einen Ton, den Sie gut singen können. Drücken Sie die Taste mit diesem Ton und singen Sie ihn. Das setzt natürlich schon die Resonanz in ihrem Innenohr voraus, sonst würden Sie den Ton nicht treffen. Als nächstes drücken Sie die Klaviertaste, aber so, dass kein Ton erklingt und halten Sie die stumme Taste nach unten gedrückt. So kann die Saite frei schwingen. Jetzt singen Sie den Ton wieder. Wenn Sie die Tonhöhe der Taste erwischt haben, dann erklingt jetzt der Ton im Klavier, ohne dass Sie die Taste erneut anschlagen. Am besten funktioniert das, wenn das Klavier offen ist, und Sie die Saiten sehen können. Aber auch bei geschlossenem Klavierdeckel funktioniert es, Sie müssen eventuell nur ein bisschen lauter singen. Sie können nun verschiedene Töne singen, z.B. eine kleine Melodie und erkennen, dass der Ton im Klavier genau dann erklingt, wenn Ihre Stimme die gleiche Tonhöhe hat wie die Taste.
Falls Sie Mühe haben, den Ton zu treffen, geht es noch einfacher. Drücken Sie auf dem Klavier das Pedal ganz rechts. Jetzt können alle Saiten frei schwingen. Rufen Sie jetzt laut auf das Klavier ein, am besten bei offenem Deckel. Wieder hören Sie, wie die Saiten schwingen, als Echo auf ihre Stimme.
Einfache Resonanz
Die «Fernwirkung» im obigen Experiment ist keine Hexerei, sondern durch Schallwellen vermittelt. Diese treten mit der Saite in Resonanz. Das typische daran ist, dass die Resonanz nicht bei jeder Frequenz auftritt, sondern genau dann, wenn die Schallwelle die Eigenfrequenz der Saite trifft. Eigenfrequenzen sind Eigenschaften von vielen physikalischen Systemen, z.B. kann auch eine Brücke eine Eigenfrequenz haben oder ein Glas, ein Stück Holz oder ein Topf. Saiten- und Blasinstrumente sind dahingehend perfektioniert, dass sie besonders gut klingen, d.h. dass ihre Eigenfrequenzen besonders kräftig und klangvoll sind.
Resonanzen höheren Grades
Wieder schlage ich ein kleines Experiment vor und wieder benötigen Sie ein Klavier, diesmal sollte es gestimmt sein.
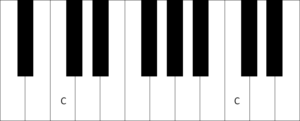
Abb 1: Zwei C’s auf dem Klavier im Abstand einer Oktave
Drücken Sie nun die Taste C auf dem Klavier, und zwar die obere (rechte) Taste C. Auf dem Klavier hat es natürlich viele von diesen C’s, nehmen Sie am besten zwei benachbarte C’s in der Mitte der Tastatur, dort ist das Experiment am deutlichsten zu hören. Sie können auch andere Töne als C’s nehmen, das Experiment funktioniert mit allen Tönen, Voraussetzung ist allerdings, dass der Abstand zwischen den beiden Tönen genau eine Oktave ist. Sie erkennen jetzt auch, woher die Oktave ihren Namen hat, das obere C ist acht (lateinisch: octo) Töne vom unteren entfernt (bei der Zählung wird für die musikalischen Intervalle der Ausgangston immer mitgezählt).
Sie haben jetzt die obere (rechte) C-Taste stumm nach unten gedrückt. Schlagen sie jetzt die untere C-Taste kurz und kräftig an. Sie hören jetzt wieder eine «Fernwirkung». Offensichtlich ist die Saite des oberen C’s durch den Anschlag des unteren in Schwingung geraten. Schlagen Sie nun eine Taste gleich links oder rechts neben dem unteren C an. Bei diesen Tasten können Sie das obere C nicht zum Klingen bringen, es entsteht keine Resonanz.
Weshalb genau bei einer Oktave eine Resonanz entsteht
Abb. 2: Mögliche Schwingungen einer Saite
In Abb. 2 sehen Sie fünf mögliche Schwingungsmuster für eine gespannte Seite. Unten (bei 1) schwingt die Saite mit genau einem Bauch in der Mitte. Bei 2 hat es zwei Bäuche, bei 5 fünf. Gelb ist die schwingende Saite gezeichnet, der schwarze Strich zeigt die korrespondierende Schallwelle, d.h. die Schallwelle (Wanderwelle), welche die gleiche Frequenz hat wie die stehende Welle, welche die klingende Saite darstellt. Diese Frequenz hat die Wellenlänge λ, ist also doppelt so lang wie die Saite.
Der Zustand 1 ist nun der Grundzustand, d.h. der Ton, der im oben vorgeschlagenen Experiment erklingt, wenn Sie eine Klaviertaste drücken. Der Zustand 2 ist der nächste erlaubte Zustand der Schwingung. Hier schwingt die Saite mit zwei Bäuchen, bei 3 sind es drei, etc. Alle Zustände also, bei denen die Saite an den Enden, an denen sie befestigt ist, nicht ausschwingt, sind Zustände, die ein ungehindertes Schwingen der Saite erlauben. Somit ist nicht nur der Zustand der einfachen Saitenschwingung möglich, sondern im Prinzip jeder, der einer Wellenlänge entspricht, die ganzzahlig in die Saitenlänge passt. Bei Zustand 2 ist die Wellenlänge halb so lang wie im Grundzustand und die Frequenz somit doppelt so gross (schnell,hoch). Zustand 2 entspricht mit seiner doppelt so grossen Frequenz dem Ton, der eine Oktave höher klingt, Zustand 4 dem Ton, der zwei Oktaven höher klingt.
Weshalb nun klingt das höhere C nun mit, wenn Sie, wie im Experiment oben vorgeschlagen, das tiefere C anschlagen? – Der Grund liegt darin, dass die Saite des tiefen C’s – wie jede Saite – nicht nur in der Grundschwingung (Zustand 1 in Abb. 2) erklingt, sondern mehr oder weniger in allen erlaubten Schwingungen. Diese Schwingungen überlagern sich also. Wenn nun die von der tieferen Saite ausgehenden Schallwellen die Saite des höheren C’s erreichen, dann enthalten sie neben der Grundschwingung immer etwas leiser auch die höheren Schwingungen und somit genau auch die Schwingung der Saite des höheren C’s. Einer Resonanz steht dadurch nichts mehr im Weg.
Sinusschwingung und Obertöne
Die schwarzen Kurve in Abb. 2 sind mathematisch gesehen Sinuskurven. Mit einem technischen Gerät ist es möglich, solche Kurven akustisch zu erzeugen, man spricht dann von einem Sinusschwingung. Mit natürlichen Klangkörpern, also der Klaviersaite, Ihrer Stimme oder überall sonst in der Natur kommen solche reinen Sinusschwingungen nicht vor, sondern die so erzeugten Schallwellen enthalten immer auch die höheren Schwingungen (Stufen 2 ff. in Abb. 2) in komplexen Überlagerungen mit. Man spricht von Obertönen. Die Anteile der einzelnen Obertöne, d.h. wie viel von den Schwingungen der Stufen 2 und folgende jeweils neben dem Grundton in der Mischung des Klangs mitschwingt, ist sehr variabel und wird von den physikalischen Eigenschaften des klangerzeugenden Mediums bestimmt. Diese Mischungen machen den Charakter des Klangs des jeweiligen Instruments aus.
Interpretation der Saitenschwingungen in den drei Welten
Platonisch → Physikalisch (Von einfach zu komplex)
Wir sehen am Beispiel der schwingenden Saite, wie mathematische Gesetzmässigkeiten aus der platonischen Welt die physikalische Welt bestimmen. In der physikalischen Welt kommen sie aber sehr verschieden an und es entsteht eine grosse Vielfalt: Auf der Saite entstehen gleichzeitig mehrere Schwingungen, neben dem Grundton entstehen immer gleichzeitig viele Obertöne. Jede einzelne dieser Schwingungen kann mathematisch sehr einfach beschrieben werden. Die Mischung jedoch ist äusserst komplex.
Was mathematisch, d.h. in der abstrakten platonischen Welt sehr einfach ist, wird schnell komplex, sobald es in der physikalischen Welt wirkt.
Die unendliche Treppe in Penrose und «Anti-Penrose»-Richtung
Die Trichter in der Skizze von Penrose stellen m.E. nur eine Richtung der Verhältnisse dar. Penrose betont in seiner Darstellung, dass nicht die ganze Mathematik gebraucht wird, um die Physik zu beschreiben und kommt so zu Mengenverhältnissen, wie sie in der Skizze mit den Trichtern dargestellt sind und die wie die ewige Treppe der Logik zu widersprechen scheinen.
Doch meines Erachtens können die Trichter auch in der Gegenrichtung gesehen werden, dann wenn man die Informationsmenge betrachtet. Diese ist in der physikalischen Welt grösser als in der platonischen. Beim Eintreten der Mathematik in die Physik entsteht Neues, nämlich die komplexe Vielfalt der Mischungsverhältnisse. Diese konkrete Vielfalt in der physikalischen Welt stellt eine Information dar, die weit über die Information der ursprünglichen mathematischen Welt hinausgeht. Die Informationsmenge nimmt in Richtung von platonisch zu physikalisch zu. Das stellt mengenmässig eine Gegenbewegung zum Trichter von Penrose dar. Die unendliche Treppe der drei Welten verliert so bei näherem Hinsehen etwas von ihrem Paradoxie-Schrecken.
Platonisch → Mental
Vermutlich haben Sie schon technisch erzeugte Sinusschwingungen gehört. Sie standen am Anfang der elektronischen Musik und hatten damals den Reiz des Neuen und Technischen. Gerade ihre nackte Reinheit war beeindruckend. Allerdings sind diese Töne sind sehr schnell auch sehr langweilig. Die Reinheit und die sterile Banalität dieser technischen Klänge ist verursacht durch das fehlende Mitschwingen der Obertöne. Die reichhaltigen Informationen dieser Zusatzschwingungen nehmen wir als Hörer wahr und sie machen den Reichtum der natürlichen Klänge aus. Ich möchte nicht auf sie verzichten.
In einem Fortsetzungsbeitrag möchte ich erklären, weshalb die Oktave in der mentalen Welt so wichtig ist und was das dazu beiträgt, dass die Tonleitern in allen Kulturen stets die Oktave als Basis haben.
Dies ist ein Beitrag zur Entstehung der Tonleitern