Schlagwort-Archive: Resonanz

Allgemein

Tonleitern

Sind unsere Tonleitern erklärbar?

Obwohl es tausende von verschiedenen Tonleitern gibt, haben alle gewisse Gemeinsamkeiten. Woher kommen diese Gemeinsamkeiten und wie sind die Tonleitern überhaupt entstanden?

Auf das Thema der Tonleitern bin ich über die Drei-Welten-Theorie nach Roger Penrose gestossen.

Die drei Welten sind:
Appendix
Drei-Welten-Theorie

Was ist Resonanz?

Hinterlassen Sie einen Kommentar

Die physikalische Basis der Resonanz

Resonanz basiert auf den Eigenschwingungen von physikalischen Medien und ihrer gegenseitigen Koppelung.

Koppelung der Eigenschwingungen von physikalischen Objekten

Die Eigenschwingungen sind stehende Wellen, deren Frequenz von den Eigenschaften des physikalischen Mediums (Grösse, Form, Material, etc. ) bestimmt wird.

Zwei solche Medien können über ihre Eigenschwingung in eine  Resonanz treten. Die Resonanz entsteht durch eine Koppelung der beiden Eigenschwingungen, sodass die beiden physikalischen Medien in ihrem Schwingungsverhalten eine gekoppelte Einheit bilden.

Die Koppelung erfolgt über einen physikalischen Energieaustausch, sei es direkt oder indirekt, z.B. über die Luft. Bedingung für das Entstehen der Koppelung ist, dass die Frequenzen der Eigenschwingungen der beiden beteiligten physikalischen Medien in einem dafür geeigneten mathematischen Verhältnis stehen.

Stabilität der Resonanz über die Zeit

Sobald der Resonanzzustand eingetreten ist, bleibt er eine gewisse Zeitspanne stabil, d.h. der gekoppelte Schwingungszustand bleibt stationär, oft über eine längere Zeit. Dieses erstaunliche Verhalten hat mit den Energieverhältnissen zu tun, die bei der Koppelung besonders energiegünstig sind.

Resonante Eigenschwingungen

Auch die Eigenschwingung eines einzelnen physikalischen Objekts kann als Resonanz bezeichnet werden. So weist z.B. ein Elektron um den Atomkern eine Resonanz mit sich selber auf und kann dadurch nur ganz bestimmte Umlauffrequenzen annehmen, die es ihm erlauben, auf seiner Umlaufbahn mit sich selber resonant zu sein. Das Gleiche gilt für das Schwingungsverhalten einer Saite.

Resonanz als Abstraktion

Das physikalische Material bestimmt zwar die Eigenfrequenz der beteiligten schwingenden Medien, doch der Rest, d.h. das Entstehen der gekoppelten Resonanz, ergibt sich aus dem geeigneten Verhältnis der beiden Frequenzen. Dieses Frequenzverhältnis folgt mathematischen Regeln. Eine verblüffend einfache Mathematik reicht aus, zu erkennen, wie stark die Resonanz zwischen den beiden schwingenden physikalischen Medien sein wird.

Drei Welten, nach Roger Penrose

Die Entstehung der Resonanz zeigt eindrücklich das Zusammenspiel von zwei der drei Welten, die gemäss Nobelpreisträger Penrose unsere Realität bilden, nämlich der physikalischen und der platonischen. Letzerer Begriff bezeichnet die abstrakte Welt der Ideen, zu der die Mathematik gehört. Mit der Verwendung des Begriffs ‹platonisch› für die Welt der Mathematik verweist Sir Penrose auf die europäische Kulturgeschichte, hier gehört die Diskussion um die Wirklichkeit und Wirksamkeit von Ideen nicht nur zur Philosophie von Platon, sondern bestimmte auch im Mittelalter als Universaliendisput grosse Teile des philosophischen Diskurses. Die Frage hat seither nichts an Relevanz verloren: Wie real sind Ideen? Warum setzt sich Abstraktes in der materiellen Welt durch? Wie ist das Verhältnis von abstrakter Idee und konkreter, d.h. physikalischer Welt?

Ich dachte vor gut einem Jahr, dass das Entstehen der Resonanz in der Musik ein gutes Beispiel wäre, um das Verhältnis von Physik, Mathematik und der dritten Welt, unserem subjektiven Empfinden zu erkunden. Ich war überrascht, wie verblüffend klar der Bezug der drei Welten hier dargestellt werden kann und wie verblüffend einfach, logisch und weitreichend die Mathematik in den Harmonien unserer Musik ist.

Resonanz in der Musik

In einem Musikstück ändern die entstehenden Resonanzen zwischen den Tönen immer wieder und bieten so einen faszinierenden Farbwechsel. Wir können ihn intuitiv erleben, aber auch rational erklären, eben als ein Spiel der Resonanzen unter den Tönen.

Nur die Obertonreihe?

In der Schule habe ich gelernt, dass die Obertonreihe unsere Tonleitern bestimmt. Doch das ist eine grobe Vereinfachung. Das Phänomen der Resonanz kann unsere Tonleitern viel einfacher und direkter erklären als es die Obertonreihe kann. Die Obertonreihe beschreibt das Schwingungsverhalten nämlich nur innerhalb eines physikalischen Medium – die in der Musik interessierende Resonanz entsteht jedoch immer zwischen mindestens zwei verschiedenen Medien (Tönen). Für die Resonanzüberlegungen von zwei Tönen müssen wir konsequenterweise auch zwei Obertonreihen vergleichen. Erst das Nebeneinanderlegen der beiden Reihen erklärt das Geschehen – ein Fakt, der in den Lehrbüchern meist übergangen wird.

Akkorde bestehen aus drei oder mehr Tönen. Auch hier kann die Resonanzanalyse der drei oder mehr beteiligten Töne die Akkordwirkung verblüffend einfach erklären. Nur müssen diesmal nicht die Frequenzen von zwei, sondern von mehreren Tönen gleichzeitig berücksichtigt werden.

Reine und temperierte Stimmung

In Europa hat sich im Barock die gleichmässig temperierte Stimmung durchgesetzt, welche die kompositorischen Möglichkeiten vielfältig erweitert. Das erste, was der Laie zur Theorie der Tonleitern findet, ist deshalb eine genaue Beschreibung der Abweichungen der temperierten von der reinen Stimmung – doch diese Abweichungen sind für die Entstehung von Resonanzen nur von marginaler Bedeutung. Die reine Stimmung ist keine Bedingung für Resonanz, die hier vorgestellte Mathematik der Resonanz erklärt das Phänomen präzis auch bei temperierter Stimmung.

Dies ist ein Beitrag zur Drei-Welten-Theorie nach Penrose und der Herkunft der Tonleitern.

Drei-Welten-Theorie

Weshalb Resonanz auch bei Unschärfe funktioniert

Hinterlassen Sie einen Kommentar

Wann entsteht Resonanz?

Resonanz zwischen zwei physikalischen Medien hängt vom Frequenzverhältnis ihrer Eigenschwingungen ab. Wenn die beiden Frequenzen einen einfachen Bruch bilden, z.B. 2/1 oder 3/2, kann Resonanz entstehen. In einem früheren Beitrag  habe ich dargestellt, wie die zehn einfachste Frequenzverhältnisse mathematisch zwingend genau zu den zehn Tönen führen, die in unseren Tonleitern vorkommen, seien es Dur, die verschiedene Molltonleitern, Kirchentonarten, Durpentatonik, Mollpentatonik, Bluestonleiter etc..

Reine und temperierte Stimmung

Funktioniert die Resonanz aber auch in der gleichstufig temperierten Stimmung? Im Beitrag zur gleichstufigen Stimmung haben wir gesehen, wie sich die beiden Stimmungen unterscheiden. Abb. 1 zeigt die die reine Stimmung in blau – d.h. die zehn resonantesten Intervalle, plus die beiden Füller Cis und Fis – und darunter die zwölf Intervalle der gleichstufig temperierten Stimmung in rot.

Abb 1: reine (blau) und gleichmässig temperierte Stimmung (rot), bei Grundton C (logarithmischer Darstellung)

Offensichtlich weichen die Frequenzverhältnisse der temperierten Stimmung von derjenigen der reinen Stimmung ab und entsprechen somit nicht mehr den einfachen Frequenzverhältnissen, welche ursprünglich zu unseren reinen Tonleitern geführt haben. Trotzdem funktioniert die unreine Stimmung und wir hören und unterscheiden kleine und grosse Terzen, Quinten und Sexten, obwohl sie gar nicht mehr rein sind. Sind die temperierten, also unreinen Intervalle dabei weiterhin resonant?

Die Antwort ist ein eindeutiges Ja.

Weshalb die unreine Stimmung trotzdem resonant ist

Abb 2. zeigt die Resonanz, abhängig, von der Frequenzrelation und der Dämpfung. Je grösser die Dämpfung ist, umso kleiner ist die Resonanz, ganz unabhängig von den Frequenzverhältnissen.

Interessant aber ist, wie die Frequenzverhältnisse – in Abb. 2 auf der Horizontalen von 0.0 bis 3.0 eingezeichnet – auf die Resonanzentstehung wirken. Am stärksten ist die Resonanz bei 1.0, also dann, wenn die beiden Medien, das anregende und das angeregte, die identische Frequenz haben. Doch auch wenn das Frequenzverhältnis nicht genau 1 ist, entsteht Resonanz. Dies ist der Grund, weshalb wir auch die temperierte Stimmung als resonant erleben.

Abb. 2: Resonanz in Abhängigkeit von der Präzision der Frequenzverhältnisse [Quelle: https://de.wikipedia.org/wiki/Resonanz (1.8.2021)] Graphikautor:  https://commons.wikimedia.org/wiki/User:Geek3]

Die temperierte Stimmung mit ihren nicht ganz genauen Brüchen führt, wie in Abb. 2 ersichtlich ist, trotzdem zu Resonanzen zwischen den Intervallen, wenn auch zu etwas schwächeren. Weil wir praktisch nur Musik hören, die auf der temperierten Stimmung basiert, haben wir uns zudem daran gewöhnt. Reine Stimmung kann nur von Stimmen und Instrumenten erklingen, welche die Tonhöhen beliebig ändern können. Auf Tasteninstrumenten geht das nicht. Reine Streicherensembles oder unbegleitete Sänger aber können rein musizieren, und gute Ensembles tun das auch.

Zusätzliche Effekte der temperierten Stimmung

Der Hauptnutzen der Temperierung liegt in einer gewaltigen Erweiterung der kompositorischen Möglichkeiten.

Es gibt aber weitere zusätzliche Effekte: Die leichte «Verstimmung» der Intervalle führt zu Interferenzen (Schwebungen). Die Resonanz kann dabei ab- und anschwellen. Die Reibung von zwei unreinen gestimmten Töne kann einen dritten entstehen lassen, der sich den beiden anderen überlagert. Solche Effekte können auch bewusst bei der reinen Stimmung gesucht werden, indem der Sänger oder Instrumentalist die Tonhöhe leicht verschiebt und damit einen bewussten musikalischen Effekt erreicht, mit dem er spielen kann.

Auf diese Effekte möchte ich aber nicht weiter eingehen. Auch nicht auf die sehr interessanten Effekte, welche Klavierstimmer beachten müssen, wie z.B. das sogenannte Strecken über den Gesamttonverlauf. Das Stimmen z.B. eines Klaviers ist muss nämlich mehrere Ziele gleichzeitig beachten. Auch dabei wirken die die drei Welten gleichzeitig: Die Mathematik der reinen Zahlen, die Physik der realen Klaviersaiten und unser subjektiver Eindruck.

Aus zwei Gründen führe ich diese Überlegungen hier aber nicht weiter. Erstens sind die genannten akustischen Phänomene sehr gut beschreiben und zweitens von Fachleuten, die sich darauf spezialisiert haben und wesentlich mehr darüber wissen als ein Informatiker und Amateurmusiker wie ich. Für mich ist die gleichstufige Temperierung einfach eine geniale und praktische Erfindung, die ich sehr gerne akzeptiere, weil sie die harmonischen Möglichkeiten der Musik deutlich erweitert.

Ich setze deshalb diese Serie mit den Erweiterungen der kompositorischen Möglichkeiten fort, die sich durch die gleichstufige Temperierung ergeben.

Dies ist ein Beitrag zum Thema Drei-Welten-Theorie.

Drei-Welten-Theorie

Zwei schlechter resonante Intervalle für die Lücken

Ausgangslage: Zwei Lücken

Im Vorbeitrag haben wir erkannt, dass in der Reihe der bisher gefundenen zehn Tonleitertönen zwei Lücken bestehen. Können wir dort auch resonante Töne finden? Folgendes wissen wir bereits:

  • Wir kennen bereits die zehn «resonantesten» Intervalle in der Oktave.
  • Mit diesen zehn Intervallen können die fünf Standard-Pentatoniken, und unser Dur und Moll gebildet werden. Dort stören die Lücken also nicht, nur in der Anordnung aller zehn potentiellen Tonleitertöne fallen sie auf.
  • Intervalle kommen nicht allein, weder in einem Akkord, noch in einer Melodie. Wenn wir also ein resonantes Intervall haben, können wir darauf ein zweites ansetzen (addieren) und das resultierende Summenintervall berechnen. Oder wir betrachten den Abstand zwischen zwei Intervallen, und rechnen dazu den Abstand zwischen den beiden Intervallen aus, zählen also das eine vom anderen ab (=Subtraktion).
  • Wegen des exponentiellen Verlaufs der Frequenzen und gegen unsere intuitive Erwartung müssen wir für das Aneinanderfügen der Intervallen ihre Frequenzverhältnisse aber nicht addieren, sondern multiplizieren, und für den Abstand dürfen wir nicht abzählen, sondern müssen dividieren.

Weil wir schon alle resonanten Intervalle innerhalb der Oktave gefunden haben, können wir für die beiden Lücken keine hochresonanten Intervalle mehr erwarten. Doch obwohl die Intervalle im Erfolgsfall zwar nicht mehr so resonant sind, was ihre Resonanz zum Grundton betrifft, sie können sie doch direkte und dadurch sehr resonante Bezüge zu anderen Tonleitertönen haben. Das macht sie im musikalischen Verbund je nach Situation ebenfalls resonanzmässig interessant.

Hier meine Versuche, Töne für die Lücken zu füllen. Zur Illustration zeige ich zu Beginn nochmals die Anordnung der zehn bestresonanten Intervalle aus dem Vorbeitrag:

Abb. 1: Anordnung der zehn resonanten Tonleitertöne in einer Oktave (logarithmische Darstellung)

Die kleinen Sekunden

Für die erste Lücke finden wir keine gute Resonanz zum Grundton, rein rechnerisch haben die Brüche dort viel zu hohe Zähler und Nenner. Der gesuchte Ton darf nur ganz wenig höher sein als der Grundton, das Intervall muss also sehr klein sein. Dazu untersuchen wir als Kandidaten die Abstände zwischen zwei Intervallen, die nahe beieinander liegen. Wir finden so:

Oktave – grosse Sept  = 2 : 15/8 = 16/15 = 1.067
Quart – grosse Terz = 4/3 : 5/4 = 16/15 = 1.067
Kleine Sext – Quint = 8/5 : 3/2 = 16/15 = 1.067
Kleine Terz – grosse Sekunde = 6/5 : 9/8 = 48/45 = 16/15 = 1.067
Grosse Terz – kleine Terz = 5/4 : 6/5 = 25/24 = 1.042
Grosse Sept – kleine Sept = 15/8 : 9/5 = 75/72 = 25/24 = 1.042
Grosse Sext – kleine Sext = 5/3 : 8/5 = 25/24 = 1.042
Kleine Sept – grosse Sext = 9/5 : 5/3 = 27/25 = 1.08

Wir finden so mehrere Intervalle, welche die Bedingungen erfüllen und in die erste Lücke passen. Wie Sie sehen, sind die Intervalle sehr klein, d.h. nur wenig grösser als 1. Mit unserer Methode tauchen immer wieder die gleichen Intervalle auf, insgesamt sind es drei, die sich aus je zwei bekannten und resonanten Intervallen herleiten lassen:

  • 16/15 = 1.042
    – grosse Terz – kleine Terz
    – grosse Sext – kleine Sext
    – grosse Sept – kleine Sept
  • 25/24 = 1.067
    – kleine Terz – grosse Sekunde
    – kleine Sext – Quint
    – Quart – grosse Terz
    – Oktave – grosse Sept
  • 27/25 = 1.08
    – kleine Sept – grosse Sext.

Diese drei Intervalle klingen alle recht scharf. Wir nennen sie kleine Sekunden. In reiner Stimmung gibt es mindestens drei davon.

Die Tritoni

Die zweite Lücke findet sich genau in der Mitte der Tonleiter. Wir versuchen nun, mit Kombination von zwei bekannten resonanten Intervallen diese Lücke zu treffen:

Grosse Sept – Quart = 15/8 : 4/3 = 45/32 = 1.406
Kleine Sept – grosse Terz = 9/5 : 5/4 = 36/25 = 1.44
Grosse Sext – kleine Terz = 5/3 : 6/5 = 25/18 = 1.389
Oktave + kleine Terz – grosse Sext = 2 x 6/5 : 5/3 = 12/5 : 5/3 = 36/25 = 1.44

Wieder erhalten wir drei Intervalle, die nahe beieinander sind:

  • 25/18 = 1.389
  • 45/32 = 1.406
  • 36/25 = 1.440

Einfügung der kleinen Sekunden und Tritoni in die Reihe der Tonleitertöne

Unsere bisherigen Berechnungen betreffen die Frequenzverhältnisse. Diese müssen wir, wie im Vorbeitrag erklärt, logarithmisch umwandeln, damit ihre Abstände dem entsprechen, was wir in unserer mentalen Welt wahrnehmen. In logarithmischer Darstellung (auf Basis 2) erhalten wir folgende Verteilung:

Abb. 2: Drei kleine Sekunden («Halbtöne») und drei Tritoni füllen die Lücken von Abb. 1

Wir sehen zwar, dass die Vorschläge die Lücken jeweils gut füllen, doch für jede Lücke haben wir drei Vorschläge! Welcher ist jetzt der beste? Wir könnten für den mit den kleinsten Zahlen in Zähler und Nenner argumentieren oder für den mit der grössten Häufigkeit unter den Varianten oder den mit dem engsten Bezug zu einer bereits bekannten Tonleiter.  Doch wir schieben die Frage mit gutem Grund bis zur Behandlung der temperierten Stimmung auf.

Dies ist ein Beitrag aus der Serie über die Tonleitern in der Drei-Welten-Theorie

Drei-Welten-Theorie, Information

Resonanz und Oktave

2 Kommentare

Dies ist ein Beitrag zur Drei-Welten-Theorie und setzt den Beitrag zur Oktave fort.

Wir erzeugen eine Resonanz

Falls Resonanz für Sie ein abstraktes – oder noch kein erlebtes musikalisches – Phänomen ist, empfehle ich Ihnen folgendes einfaches Experiment: Suchen sie ein Klavier (kein digitales) und auf dem Klavier einen Ton, den Sie gut singen können. Drücken Sie die Taste mit diesem Ton und singen Sie ihn. Das setzt natürlich schon die Resonanz in ihrem Innenohr voraus, sonst würden Sie den Ton nicht treffen. Als nächstes drücken Sie die Klaviertaste, aber so, dass kein Ton erklingt und halten Sie die stumme Taste nach unten gedrückt. So kann die Saite frei schwingen. Jetzt singen Sie den Ton wieder. Wenn Sie die Tonhöhe der Taste erwischt haben, dann erklingt jetzt der Ton im Klavier, ohne dass Sie die Taste erneut anschlagen. Am besten funktioniert das, wenn das Klavier offen ist, und Sie die Saiten sehen können. Aber auch bei geschlossenem Klavierdeckel funktioniert es, Sie müssen eventuell nur ein bisschen lauter singen. Sie können nun verschiedene Töne singen, z.B. eine kleine Melodie und erkennen, dass der Ton im Klavier genau dann erklingt, wenn Ihre Stimme die gleiche Tonhöhe hat wie die Taste.

Falls Sie Mühe haben, den Ton zu treffen, geht es noch einfacher. Drücken Sie auf dem Klavier das Pedal ganz rechts. Jetzt können alle Saiten frei schwingen. Rufen Sie jetzt laut auf das Klavier ein, am besten bei offenem Deckel. Wieder hören Sie, wie die Saiten schwingen, als Echo auf ihre Stimme.

Einfache Resonanz

Die «Fernwirkung» im obigen Experiment ist keine Hexerei, sondern durch Schallwellen vermittelt. Diese treten mit der Saite in Resonanz. Das typische daran ist, dass die Resonanz nicht bei jeder Frequenz auftritt, sondern genau dann, wenn die Schallwelle die Eigenfrequenz der Saite trifft. Eigenfrequenzen sind Eigenschaften von vielen physikalischen Systemen, z.B. kann auch eine Brücke eine Eigenfrequenz haben oder ein Glas, ein Stück Holz oder ein Topf. Saiten- und Blasinstrumente sind dahingehend perfektioniert, dass sie besonders gut klingen, d.h. dass ihre Eigenfrequenzen besonders kräftig und klangvoll sind.

Resonanzen höheren Grades

Wieder schlage ich ein kleines Experiment vor und wieder benötigen Sie ein Klavier, diesmal sollte es gestimmt sein.

Abb 1: Zwei C’s auf dem Klavier im Abstand einer Oktave

Drücken Sie nun die Taste C auf dem Klavier, und zwar die obere (rechte) Taste C. Auf dem Klavier hat es natürlich viele von diesen C’s, nehmen Sie am besten zwei benachbarte C’s in der Mitte der Tastatur, dort ist das Experiment am deutlichsten zu hören. Sie können auch andere Töne als C’s nehmen, das Experiment funktioniert mit allen Tönen, Voraussetzung ist allerdings, dass der Abstand zwischen den beiden Tönen genau eine Oktave ist. Sie erkennen jetzt auch, woher die Oktave ihren Namen hat, das obere C ist acht (lateinisch: octo) Töne vom unteren entfernt (bei der Zählung wird für die musikalischen Intervalle der Ausgangston immer mitgezählt).

Sie haben jetzt die obere (rechte) C-Taste stumm nach unten gedrückt. Schlagen sie jetzt die untere C-Taste kurz und kräftig an. Sie hören jetzt wieder eine «Fernwirkung». Offensichtlich ist die Saite des oberen C’s durch den Anschlag des unteren in Schwingung geraten. Schlagen Sie nun eine Taste gleich links oder rechts neben dem unteren C an. Bei diesen Tasten können Sie das obere C nicht zum Klingen bringen, es entsteht keine Resonanz.

Weshalb genau bei einer Oktave eine Resonanz entsteht

Grundton und Obertöne

Abb. 2:  Mögliche Schwingungen einer Saite
In Abb. 2 sehen Sie fünf mögliche Schwingungsmuster für eine gespannte Seite. Unten (bei 1) schwingt die Saite mit genau einem Bauch in der Mitte. Bei 2 hat es zwei Bäuche, bei 5 fünf. Gelb ist die schwingende Saite gezeichnet, der schwarze Strich zeigt die korrespondierende Schallwelle, d.h. die Schallwelle (Wanderwelle), welche die gleiche Frequenz hat wie die stehende Welle, welche die klingende Saite darstellt. Diese Frequenz hat die Wellenlänge λ, ist also doppelt so lang wie die Saite.

Der Zustand 1 ist nun der Grundzustand, d.h. der Ton, der im oben vorgeschlagenen Experiment erklingt, wenn Sie eine Klaviertaste drücken. Der Zustand 2 ist der nächste erlaubte Zustand der Schwingung. Hier schwingt die Saite mit zwei Bäuchen, bei 3 sind es drei, etc. Alle Zustände also, bei denen die Saite an den Enden, an denen sie befestigt ist, nicht ausschwingt, sind Zustände, die ein ungehindertes Schwingen der Saite erlauben. Somit ist nicht nur der Zustand der einfachen Saitenschwingung möglich, sondern im Prinzip jeder, der einer Wellenlänge entspricht, die ganzzahlig in die Saitenlänge passt. Bei Zustand 2 ist die Wellenlänge halb so lang wie im Grundzustand und die Frequenz somit doppelt so gross (schnell,hoch). Zustand 2 entspricht mit seiner doppelt so grossen Frequenz dem Ton, der eine Oktave höher klingt, Zustand 4 dem Ton, der zwei Oktaven höher klingt.

Weshalb nun klingt das höhere C nun mit, wenn Sie, wie im Experiment oben vorgeschlagen, das tiefere C anschlagen? – Der Grund liegt darin, dass die Saite des tiefen C’s – wie jede Saite – nicht nur in der Grundschwingung (Zustand 1 in Abb. 2) erklingt, sondern mehr oder weniger in allen erlaubten Schwingungen. Diese Schwingungen überlagern sich also. Wenn nun die von der tieferen Saite ausgehenden Schallwellen die Saite des höheren C’s erreichen, dann enthalten sie neben der Grundschwingung immer etwas leiser auch die höheren Schwingungen und somit genau auch die Schwingung der Saite des höheren C’s. Einer Resonanz steht dadurch nichts mehr im Weg.

Sinusschwingung und Obertöne

Die schwarzen Kurve in Abb. 2 sind mathematisch gesehen Sinuskurven. Mit einem technischen Gerät ist es möglich, solche Kurven akustisch zu erzeugen, man spricht dann von einem Sinusschwingung. Mit natürlichen Klangkörpern, also der Klaviersaite, Ihrer Stimme oder überall sonst in der Natur kommen solche reinen Sinusschwingungen nicht vor, sondern die so erzeugten Schallwellen enthalten immer auch die höheren Schwingungen (Stufen 2 ff. in Abb. 2) in komplexen Überlagerungen mit. Man spricht von Obertönen. Die Anteile der einzelnen Obertöne, d.h. wie viel von den Schwingungen der Stufen 2 und folgende jeweils neben dem Grundton in der Mischung des Klangs mitschwingt, ist sehr variabel und wird von den physikalischen Eigenschaften des klangerzeugenden Mediums bestimmt. Diese Mischungen machen den Charakter des Klangs des jeweiligen Instruments aus.

Interpretation der Saitenschwingungen in den drei Welten

Platonisch → Physikalisch (Von einfach zu komplex)

Wir sehen am Beispiel der schwingenden Saite, wie mathematische Gesetzmässigkeiten aus der  platonischen Welt die physikalische Welt bestimmen. In der physikalischen Welt kommen sie aber sehr verschieden an und es entsteht eine grosse Vielfalt: Auf der Saite entstehen gleichzeitig mehrere Schwingungen, neben dem Grundton entstehen immer gleichzeitig viele Obertöne. Jede einzelne dieser Schwingungen kann mathematisch sehr einfach beschrieben werden. Die Mischung jedoch ist äusserst komplex.

Was mathematisch, d.h. in der abstrakten platonischen Welt sehr einfach ist, wird schnell komplex, sobald es in der physikalischen Welt wirkt.

Die unendliche Treppe in Penrose und «Anti-Penrose»-Richtung

Die Trichter in der Skizze von Penrose stellen m.E. nur eine Richtung der Verhältnisse dar. Penrose betont in seiner Darstellung, dass nicht die ganze Mathematik gebraucht wird, um die Physik zu beschreiben und kommt so zu Mengenverhältnissen, wie sie in der Skizze mit den Trichtern dargestellt sind und die wie die ewige Treppe der Logik zu widersprechen scheinen.

Doch meines Erachtens können die Trichter auch in der Gegenrichtung gesehen werden, dann wenn man die Informationsmenge betrachtet. Diese ist in der physikalischen Welt grösser als in der platonischen. Beim Eintreten der Mathematik in die Physik entsteht Neues, nämlich die komplexe Vielfalt der Mischungsverhältnisse. Diese konkrete Vielfalt in der physikalischen Welt stellt eine Information dar, die weit über die Information der ursprünglichen mathematischen Welt hinausgeht. Die Informationsmenge nimmt in Richtung von platonisch zu physikalisch zu. Das stellt mengenmässig eine Gegenbewegung zum Trichter von Penrose dar. Die unendliche Treppe der drei Welten verliert so bei näherem Hinsehen etwas von ihrem Paradoxie-Schrecken.

Platonisch → Mental

Vermutlich haben Sie schon technisch erzeugte Sinusschwingungen gehört. Sie standen am Anfang der elektronischen Musik und hatten damals den Reiz des Neuen und Technischen. Gerade ihre nackte Reinheit war beeindruckend. Allerdings sind diese Töne sind sehr schnell auch sehr langweilig. Die Reinheit und die sterile Banalität dieser technischen Klänge ist verursacht durch das fehlende Mitschwingen der Obertöne. Die reichhaltigen Informationen dieser Zusatzschwingungen nehmen wir als Hörer wahr und sie machen den Reichtum der natürlichen Klänge aus. Ich möchte nicht auf sie verzichten.

In einem Fortsetzungsbeitrag möchte ich erklären, weshalb die Oktave in der mentalen Welt so wichtig ist und was das dazu beiträgt, dass die Tonleitern in allen Kulturen stets die Oktave als Basis haben.

Dies ist ein Beitrag zum Thema Drei-Welten-Theorie.

 

Drei-Welten-Theorie, Information

Die Oktave

Hinterlassen Sie einen Kommentar

Eine bemerkenswerte Gemeinsamkeit

Alle Tonleitern, die ich kenne, bewegen sich im Bereich einer Oktave. Auch Tonleitern, die für uns Europäer ungewöhnlich klingen, arabische, indische, japanische und afrikanische bewegen sich innerhalb genau einer Oktave, d.h. ihr tiefster und ihr höchster Ton haben den Abstand von genau einer Oktave, was für eine Tonart das auch ist.

Ich finde das äusserst bemerkenswert. Das ist so, als ob alle Sprachen der Welt, die ja sehr unterschiedliche Wörter haben, für einen bestimmten Begriff das gleiche Wort verwenden würden, und zwar schon immer und ganz unabhängig voneinander. Woher kommt das?

Die Drei-Welten-Theorie kann nun diese ungewöhnliche Gemeinsamkeit der Tonarten aller menschlichen Kulturen plausibel erklären.

Die Oktave platonisch

Wenn Sie eine Saite auf einer Geige zupfen, erhalten Sie einen Ton. Wenn Sie nun den Finger genau in der Mitte der Saite auf das Griffbrett drücken und dann zupfen, erklingt die Saite eine Oktave höher. Das gleiche gilt für Pfeifen. Eine Pfeife, die halb so lang ist wie eine andere, klingt eine Oktave höher. Offensichtlich liegt der Oktave ein Verhältnis 1:2 zugrunde. Das ist die platonische, d.h. mathematische Seite der Oktave. Einfache mathematischen Verhältnisse (= Brüche) spielen auch bei anderen Intervallen eine Rolle, worauf wir noch kommen werden.

Diese mathematischen Verhältnisse der Verhältnisse zwischen den Tönen – das heisst der Intervalle – sind schon lange bekannt und wurden vom Griechen Pythagoras gelehrt, der vor Sokrates und Platon eine einflussreiche Schule in Süditalien begründete.

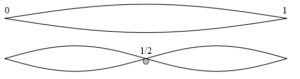
Abb. 1: Eine schwingende Saite. Oben ist die Saite links und rechts (0 und 1) befestigt, kann dort also nicht schwingen. Je weiter weg von der Befestigung, umso stärker schwingt sie aus, am meisten in der Mitte. Unten ist in der Mitte ein Finger auf die Seite gedrückt, und sie schwingt nun in der halben Länge und eine Oktave höher. (Mit diesen Beschreibungen sind wir aber von der platonischen bereits in die physikalischen Welt eingetreten).

Das einfaches Zahlenverhältnis erklärt die Einzigartigkeit des gemeinsamen Merkmals Oktave über alle menschlichen Kulturen noch nicht. Weshalb spielt das Zahlenverhältnis für die Tonleitern überhaupt eine Rolle?

Zur Erklärung müssen wir die beiden anderen Welten ansehen, nämlich die physikalische, in der Töne erklingen, und die mentale, in der wir sie wahrnehmen.

Die Oktave physikalisch

Töne

Töne sind materielle Schwingungen in einem Trägermedium, z.B. Luft. Ein Ton enthält ist in der Regel eine Überlagerung von mehreren Schwingungen (Grundton plus Obertöne). An dieser Stelle schauen wir aber nur die Grundschwingung an, die die erkennbare Tonhöhe bestimmt.

Diese Grundschwingung ist eine Sinuskurve und die Tonhöhe wird als Frequenz angegeben, z.B. 440 Hz. Diese Frequenz bedeutet, dass die Sinuskurve 440 mal pro Sekunde hin und her schwingt. Das gleiche tut auch die Saite.

Die Saite schwingt an Ort, man spricht von einer stehenden Welle (siehe Abb. 1 oben). Die Schwingung in der Luft hingegen bewegt sich vom Ort fort (Wanderwelle). Durch ihre stationären Schwingung kann die Saite die Luft bewegen und führt so zu einer Schwingung in der Luft, einer Schallwelle. Dabei überträgt die Saite die Eigenschaften ihrer Schwingung, insbesondere deren Frequenz, auf die Schallwelle.

Die Wellenlänge in einer Wanderwelle, also einer Schallwelle, aber auch z.B. einer Welle auf der Wasseroberfläche ist der Abstand der Wellenbäuche (oder Wellenkämme)  voneinander. Bei einer stehenden Welle, also der Saite in Abb. 1 ist die Wellenlänge gleich der (doppelten) Länge der schwingenden Saite.

Wenn nun die Geschwindigkeit der Wanderwelle konstant ist, dann müssen mehr Wellenbäuche hintereinander kommen, je kürzer die Abstände zwischen ihnen sind. Die Abstände zwischen den Wellenkämmen entsprechen der Wellenlänge, die Zahl der Kämme pro Zeit der Frequenz der Welle. Je mehr Kämme an einem Ort durchlaufen, umso kleiner sind ihre Abstände.

Zwischen der Wellenlänge und ihrer Frequenz besteht somit ein umgekehrt proportionales Verhältnis, d.h. je kürzer die Wellenlänge umso höher muss die Frequenz sein. Deshalb schwingt die halb so lange Saite doppelt so schnell. Das ist der physikalische Ursprung der Oktave.

Tonentstehung

Wie kommt nun die Schwingung in die Saite? Dies rührt daher, dass eine gespannte Saite eine Tendenz zu einer Eigenschwingung hat, Die Spannung der Saite führt dazu, dass ein Anstoss, z.B. ein Zupfen der Saite, in ihr eine Bewegung auslöst, die an den beiden Enden der Saite nicht aufhört, sondern wieder zurück gestossen wird. Auf diese Weise bildet sich die stehende Welle aus. Die Wellenlänge, also der Abstand der Wellenbäuche, wird dabei von der Länge der Saite bestimmt. Der Grund dafür ist, dass an den beiden Enden der Saite keine Bewegung mehr möglich ist, da sie ja dort fest fixiert ist. Ausschwingen kann die Welle nur dazuwischen. Die Wellenlänge muss also genau in die Länge der Saite passen.

Die Oktave mental

Das Innenohr

Wir nehmen Töne mit unseren beiden Innenohren wahr. Diese sind äusserst raffiniert gebaute Organe mit einer schneckenförmigen Struktur, weshalb man auch von der Hörschnecke spricht. Die Schallwelle durchwandert von aussen her die flüssigkeitsgefüllte Hörschnecke und erzeugt durch Resonanz eine Schwingung der sogenannten Basilarmembran, welche  die gesamte Schnecke durchzieht. Entlang der Basilarmembran nehmen sogenannte Haarzellen die Schwingungen der Basilarmembran auf und leiten sie als elektrische Signale nach innen ins Hirn. Durch den komplexen und raffinierten Bau der Schnecke, der hier nur kursorisch beschrieben ist, können die akustischen Signale analytisch zerlegt werden, sodass je nach Frequenz unterschiedliche Haarzellen angeregt werden, je höher die Frequenz umso näher am Eingang der Schnecke, je tiefer umso mehr im Innern.

Die Tonwahrnehmung mental

Bis hier hat die Beschreibung der Tonwahrnehmung über das Innenohr noch nichts mit der mentalen Welt zu tun, es handelt sich nur um die anatomischen Voraussetzungen, d.h. den physikalischen Apparat, der die physikalischen Signale (die Schallwellen) gezielt für die eigentliche Wahrnehmung vorbereitet. Diese findet im Gehirn statt und ist ein subjektiver Vorgang.

Subjektive Vorgänge zeichnen sich dadurch aus, dass sie nicht von aussen nachvollzogen werden können. Wie Sie etwas hören und empfinden, weiss ich nicht, das ist ganz Ihre Welt. Allerdings haben wir als Menschen so viele Gemeinsamkeiten, dass ich in davon ausgehen kann, dass Sie vieles ganz ähnlich erleben wie ich. Wir haben die gleiche Anatomie und die gleichen Lebensbedingungen. Weshalb empfinden viele Menschen die gleiche Musik als schön? Wenn wir von der gleichen Musik gerührt werden, sie gleich wie andere als fröhlich, traurig, tröstend, mitreissend usw. empfinden, zeigt das, dass unsere mentalen Welten trotz ihrer Subjektivität stark verbunden sind.

Dabei spielen kulturelle Aspekte – also gelernte Gewohnheiten – eine ganz wichtige Rolle. Auch die Kultur gehört letztlich in die mentale Welt, sie ist der Geist, d.h. die Subjektivität, die wir teilen. Diese Subjektivität, die individuelle wie die kollektive, fusst aber auch auf den physikalischen Voraussetzungen.

Somit sind wir wieder bei unserem Thema: Weshalb haben alle Kulturen der Menschen die Oktave in ihren sonst so verschiedenen Tonleitern?

Der Grund ist physikalisch erklärbar und liegt in der Resonanz.

Die Resonanz

Resonanz ist eine Voraussetzung, dass die Töne im Innenohr überhaupt ankommen. Denn die Basilarmembran im Innenohr übernimmt die Schwingungen der Schallwellen auf eine ganz bestimmte Weise. Nicht alle Frequenzen finden auf der Basilarmembran die gleiche Resonanz. Das Innenohr ist so gebaut, dass die Basilarmembran am Eingang mit hohen Frequenzen in Resonanz gerät und in der Tiefe mit tiefen. So analysiert das Ohr die verschiedenen Tonhöhen. Aber die Resonanz ist noch für viel mehr verantwortlich, u.a. auch dafür, dass in den tausenden unterschiedlichen Tonleitern die Oktave immer vorkommt. Dieser auffällige Beobachtung werden wir im Fortsetzungsbeitag verfolgen.

Dies ist ein Beitrag zur Drei-Welten-Theorie.

 

Allgemein

Tonleitern (Übersichtsseite)

1 Kommentar
Wie Tonleitern entstehen: Musik in drei Welten

Die Weltkultur und unsere eigene europäische Musikkultur kennen unzählige verschiedene Tonleitern. Trotz dieser Vielfalt weisen alle Tonleitern auch Ähnlichkeiten auf.  Wie lassen sich Gemeinsamkeiten und Unterschiede erklären?

Resonanz und Musik: Eine Übersicht

Naturwissenschaftler und Musiker leben in verschiedenen Welten. Das Thema Resonanz ist jedoch für beide Welten relevant. Hier finden Sie eine kurze Übersicht:

Appendix
Youtube-Demo zum Quintenexperiment

Die Quinte ist kein Oberton. Trotzdem gibt es eine starke Resonanz über dieses Intervall. Eine kurze Demonstration der Resonanz über eine Quinte finden  Sie hier.

Die Erklärung der Tonleitern in LDC

LDC ist eine neue Möglichkeit, komplexe Sachverhalte und Diskussionen abzubilden.  Sehen Sie, wie damit die Theorie der Tonleitern erklärt werden kann. -> Tonleitern in LDC

Philosophischer Background: Drei Welten

Realität lässt sich unter verschiedenen Perspektiven anschauen. Roger Penrose spricht von drei-Welten:

  • Die platonische Welt enthält zeitlose und nicht an einem bestimmten Punkt befindliche Objekte, z.B. mathematische Elemente und abstrakte Muster.
  • Die physikalische Welt hat Raum und Zeit und lässt sich von aussen genau beschreiben,
  • Die mentale Welt ist die Welt in unseren Köpfen, also das, was wir denken, fühlen und erleben.

Es ist klar, dass für die Musik alle drei Welten eine Rolle spielen. Ganz offensichtlich ist das auch für die Tonleitern der Fall.

Der Autor als Pianist

Sie kennen mich möglicherweise als Informatiker und fragen sich, weshalb ich hier über Musiktheorie schreibe. In der Tat verbringe ich seit jeher viel Zeit am Klavier. Hier zwei Hörbeispiele:

«Billie’s Bounce»
Live im Restaurant Zeppelin, Konstanz am 5. Dez. 2008.
Tenorsaxophon: Bruce Roberts, UK.
Vibraphon: Christoph Mantels, DE.
Klavier: Hansruedi Straub.
Kontrabass: Samuel Forrer.
Drums: Urs Heinrich.

 

«Body and Soul»
Live in Bühler, AI, 2015.
Klavier: Hansruedi Straub.
Kontrabass: Samuel Forrer.
Drums: Urs Heinrich.