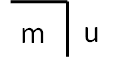Schlagwort-Archive: Spencer-Brown

Information

Entropie: Schlüssel zur Informationstheorie

Entropie: Schlüsselbegriff der Informationstheorie

Entropie ist der Schlüssel, um zu verstehen, was Information bedeutet. Seit Claude Shannons «The Mathematical Theory of Communication» ist evident, dass die Bits der Entropie und die Bits der Information das gleiche messen.

Doch was ist Entropie? Der Zusammenhang zwischen Entropie und Information ist den meisten unbekannt. Gerade  deshalb lohnt sich ein genauerer Blick.

Was ist Entropie?

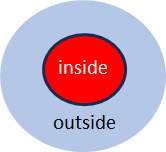
Die gängige Vorstellung von Entropie, nimmt sie als ein Mass für das Chaos. Wie aber kann ein Mass für Chaos ein Mass für Information sein? Chaos und Information sind doch offensichtlich nicht das gleiche! – Das scheinbare Paradox löst sich auf, sobald die moderne Definition von Entropie (nach C.F. von Weizsäcker), zu Grunde gelegt wird. Diese definiert Entropie als Abstand zwischen zwei Beschreibungsebenen:

Was hat Entropie mit Information zu tun?

Der Unterschied zwischen der Beschreibung auf der Mikro- und derjenigen auf Makroebene definiert beides, die Information und die Entropie. Entropie wird dadurch eine relative Grösse, die als Abstand, d.h. als Differenz gemessen und in Bits gemessen werden kann.

Genau das gleiche trifft auf Information zu. Auch Information ist eine relative Grösse, nämlich der Abstand zwischen Wissen und Unwissen:

Entropie ist mehr als Wärmelehre

Der Begriff Entropie stammt ursprünglich aus der Wärmelehre und ergänzt dort den Begriff der Energie. Entropie ist aber viel mehr, nämlich als Informationsentropie nach Claude Shannon auch ein Mass für Information.  Die zugehörige Masseinheit ist das Bit. Trotz seiner enormen Bedeutung in der Physik, der Informationstheorie, aber auch im Alltag, gilt der Begriff der Entropie als nerdig und kaum verständlich. Das wäre nicht nötig.

Fünf weit verbreitete Vorurteile erschweren das Verständnis dieses wichtigen Begriffs in der Physik und im Alltag:

Bits und ihr Kontext

In der Informationstheorie gelten Bits als Grundlage der Information. Bits und Entropie hängen eng zusammen, wie Shannon in seinem Schlüsselwerk ‹The Mathematical Theory of Communication› aufgezeigt hat.

Die Entropie spielt aber auch eine Rolle bei der Beschreibung des Kontexts eines Bits. Erst durch den Einbezug des Kontextes erhalten die Bits ihre Bedeutung.  Etwas überspitzt könnte man sagen, dass das Bit ohne seinen Kontext keine Bedeutung hat.

Bits müssen ihre Bedeutung stets von aussen erhalten. Wenn der Kontext unklar ist, ist die Präzision der Bits irreführend. Wenn er klar ist, kann man mit Bits jedoch sehr praktisch rechnen.

Das Bit und die Unterscheidung nach Spencer-Brown

Eine Alternative bezüglich der Behandlung des Kontextes ist der Begriff der Unterscheidung (Distinction) nach Spencer-Brown.

Spencer-Browns Distinction gleicht zwar als binärer Grundbaustein dem Bit, unterscheidet sich von ihm aber dadurch, dass der unlimitierte(!) Kontext in diesen Grundbaustein einbezogen ist. Dadurch wird das Rechnen mit diesem Grundbaustein aber auch schwieriger und deshalb hat er sich in der technischen Welt nicht durchgesetzt – ganz im Gegensatz zum technisch gut isolierbaren und in Kalkulationen perfekt einsetzbaren Bit.

Entropie ist überall

Stanislaw Lem hat in den 70-er Jahren des letzten Jahrhunderts viele Theme der 20-er Jahre dieses Jahrhunderts vorweggenommen. Nicht zuletzt das Thema der künstlichen Intelligenz. Seine philosophischen Überlegungen dazu sind heute topaktuell. Doch auch zur Entropie hat er sich auf originelle Weise geäussert:

Informationsreduktion

Mit der Entropie eng verbunden ist das Phänomen der Informationsreduktion.

Logische Systeme sind immer Vereinfachungen der viel komplexeren und detailhaltigeren Realität. Um zu verstehen, wie wir denken, müssen wir uns mit dieser notgeborenen und unausweichlichen Beschränkung unseres Wissens um die Realität abfinden. Zu diesem natürlichen Vorgang der Informationsreduktion habe ich ab 2019 eine kleine Beitragsserie geschrieben:

Das Thema der Informationsreduktion irritiert viele,  doch wir befinden uns damit auf den Spuren von zwei der wichtigsten europäischen Philosophen, nämlich von William Ockham (Ockhams Razor) und Sokrates (Ich weiss, dass ich nichts weiss).

Entropie wird in Bits gemessen und ist eine der Grundlagen von Information -> Übersichtsseite Informationstheorie

 

Logik

Logik

Ist Logik statisch oder dynamisch?

Viele denken, dass unsere abendländische Logik perfekt sei. Sie hat sich über viele Jahrhunderte um das Beweisen bemüht, angefangen von den Syllogismen des Aristoteles über die Gottesbeweise der mittelalterlichen Scholastik bis hin zur First-Order-Logic der Mathematik in jüngerer Zeit.  Diese Systeme sind trotz ihres reifen Entwicklungsgrades nicht ausreichend, um die dynamischen Prozesse des Denkens abzubilden.

Dies fängt bereits mit dem einfachen IF-THEN an, das in den Syllogismen und der First-Order-Logic aus Prinzip immer statisch ist. Eine dynamische Logik ist jedoch unabdingbar, um Denkprozesse präzis zu beschreiben.

Non-Monotonic Reasoning

Die klassische Logik ist monoton. Um die Denkprozesse abzubilden bedarf es aber einer nicht-monotonen, d.h. dynamischen Logik:

  • NMR (Non-Monotonic-Reasoning)

Das Festhalten an der monotonen Logik ist bedauerlich und führt in der Konsequenz dazu, dass die Universitäten gerade in ihrem Kernbereich Logik nicht in der Lage sind, das Leben zu verstehen.

Die monotone Logik – d.h. die First-Order-Logik – ist zu rigid, um Lebensprozesse abzubilden.

Selbstreferentialität bricht klassische Logik

Ein Problem der konventionellen Logik liegt in der Schlaufe der Selbstreferentialität (Barbierparadox, Gödel, Spencer-Brown).

Dazu habe ich 2015 zwei Texte notiert:

Selbstreferentialität bricht den Zeitfluss und kann zu den klassischen Paradoxen führen:

Information, Logik

Paradoxe Logikkerne (Teil 2)

Hinterlassen Sie einen Kommentar

Dieser Beitrag setzt Paradoxe Logikkerne (Teil 1) fort

«Draw a Distinction»

Mit diesen Worten führt Spencer-Brown den elementaren Baustein seiner formalen Logik ein: «Draw a Distinction» – «Zieh eine Unterscheidung». Abbildung 1 zeigt dieses sehr einfache Element der Unterscheidung oder Distinction, den formalen Baustein von Spencer-Browns Logik:

Abb 1: Die Form der Unterscheidung von Spencer-Brown

Eine extreme Abstraktion

In der Tat besteht seine Logik ausschliesslich aus diesem Baustein. Spencer-Brown ist damit eine Abstraktion gelungen, die abstrakter ist als alles, was Mathematiker und Logiker bisher gefunden hatten.

Was ist mit dieser Form nun gemeint? Spencer-Brown zielt auf einen elementaren Prozess, nämlich das ‹Ziehen einer Unterscheidung›. Dieser elementare Prozess teilt nun die Welt in zwei Teile, nämlich den Teil, der innerhalb der Unterscheidung liegt, und den Teil ausserhalb.


Abb. 2: Visualisierung der Unterscheidung

Die Teilung der Welt

Abbildung 2 zeigt, was das formale Element von Abb 1 meint: eine Teilung der Welt in das Unterschiedene (inside) und alles andere (outside). Der Winkel von Abb. 1 wird also – gedanklich – zum Kreis, der alles einschliesst, was gemeint, also unterschieden («draw a distinction») ist.

Die Winkelform von Abb. 1 meint also den Zirkel von Abb. 2, der alles umfasst, was gemeint ist.

Perfekte Beinhaltung

Weshalb aber zeichnet Spencer-Brown seinen elementaren Baustein als offenen Winkel und nicht als geschlossenen Kreis, obwohl er die Geschlossenheit meint, indem er ausdrücklich sagt: «Distinction is perfect continence», der Unterscheidung also eine perfekte Beinhaltung zuweist. Dass er trotzdem die Beinhaltung als Winkel zeigt, wird später klar werden, und sich als eine von Spencer-Browns genialen Entscheidungen erweisen. (mehr dazu im iommenden Beitrag «Imaginärer Logikwert»)

Unterscheidung von Markiert und Unmarkiert

Zudem ist es möglich, die Innenseite und die Aussenseite zu benennen, als den markierten (m=marked) und den unmarkierten (u=unmarked) Raum und diese Benennungen später in grösseren Kombination von Unterscheidungen zu verwenden.

Abb. 3: Marked (m) und unmar​ked (u) space

Kombinatierte Unterscheidungen

​​Um den Baustein in grösseren Logikaussagen zu verwenden, kann er nun auf verschiedene Weisen zusammengestellt werden.

Abb. 4: Drei kombinierte Formen der Unterscheidung

Abbildung 4 zeigt, wie Unterscheidungen auf zwei Arten miteinander kombiniert werden können, entweder als Aufzählung (seriell) oder als Etagierung, indem über Unterscheidungen weitere Unterscheidungen gestellt werden. Spencer Brown arbeitet mit diesen Kombinationen und leitet – ganz Mathematiker – verschiedene Schlüsse und Beweise aus wenigen Axiomen und Kanons ab. Er baut auf diese Weise ein eigenes formales mathematisch-logisches Regelwerk auf. Die Ableitungen und Beweise müssen uns hier nicht vordringlich interessieren, sie zeigen aber, wie sorgfältig und mathematisch-penibel Spencer-Brown seinen Formalismus entwickelt.

​Re-Entry

Das Re-Entry, der Wiedereintritt ist nun das, was uns zum Paradox führt. Es ist nun in der Tat so, dass Spencer-Browns Formalismus es möglich macht, den Formalismus echter Paradoxe, wie z.B des Barbierparadoxes auf ganz einfache Weise zu zeichnen. Das Re-Entry wirkt wie ein leuchtender Edelstein (sorry für die poetische Ausdrucksweise), der in logischen Netzen eine ganz spezielle Funktion übernimmt, nämlich die Verknüpfung von zwei logischen Ebenen, einer Basisebene und ihrer Metaebene.

Der Trick dabei ist, dass auf beiden Ebenen die gleiche Unterscheidung getroffen wird. Dass es sich also um die gleiche Unterscheidung handelt, aber auf zwei Ebenen, und dass sich diese eine Unterscheidung auf sich selber bezieht, von der einen Ebene auf die andere, von der Metaebene auf die Basisebene. Das ist die Form der Paradoxie.

Beispiel Barbierparadox

Wir können nun das Barbierparadox mit Hilfe der Form von Spencer-Brown notieren:

Abb. 5: Unterscheidung der Männer des Dorfes, die
sich selber (S) oder nicht selber (N) rasieren

​

Abb. 6: Notation von Abb. 5 als perfekte Beinhaltung

Abb. 5 und Abb. 6 zeigen das gleiche, nämlich die Unterscheidung der Männer des Dorfes in solche, die sich selber rasieren und die anderen, die das nicht tun.

Wie kommt nun der Barbier hinein? Nehmen wir an, er ist eben aufgestanden und noch unrasiert. Dann gehört er zur Innenseite der Unterscheidung, also zur Gruppe der unrasierten Männer N. Kein Problem für ihn, er rasiert sich schnell, frühstückt und geht dann an die Arbeit. Jetzt gehört er zu den Männern S, die sich selber rasieren, er muss sich also nicht mehr rasieren. Das Problem stellt sich erst am nächsten Morgen. Jetzt gehört er ja zu den Männern, die sich selber rasieren – also muss er sich nicht rasieren. Unrasiert, wie er ist, muss er sich aber jetzt rasieren. Sobald er sich aber rasiert, gehört er zur Gruppe der Selberrasierer, muss sich also nicht rasieren. So wechselt der Barbier von einer Gruppe in die andere. Es stellt sich das typische Oszillieren des Barbierparadoxes – und auch aller anderen echten Paradoxien ein, die alle oszillieren.
​

Wie entsteht das Paradox?

​

Abb. 7: Der Barbier (B) rasiert alle Männer, die sich
nicht selber rasieren (N)

Abb. 7 zeigt als Basis die Unterscheidung der Männer N (rot)  und S (blau). Das ist die Basisebene. Nun kommt der Barbier (B) hinein. Auf einer logischen Metaebene wird ausgesagt, dass er die Männer N rasiert, in Abb. 7 durch den Pfeil symbolisiert.

Das Paradox entsteht zwischen der Basis- und der Metaebene. Dann nämlich, wenn gefragt wird, ob der Barbier, der ja auch ein Mann des Dorfes ist, zur Menge N oder zur Menge S gehört. Mit anderen Worten:

→ Ist  B  ein  N  oder ein  S ?

​Wenn B ein N ist, dann rasiert er sich (Abb. 7). Dadurch wird er zu einem S, also rasiert er sich nicht. Dadurch wird er zum N und rasiert sich. Das ist das Paradox und seine Oszillation.

Wie entsteht sie? Indem die beiden Ebenen verknüpft werden. Der Barbier ist ein Element der Metaebene, aber gleichzeitig ein Element der Basisebene. Der Barbier B ist auf der Metaebene ein handelndes Subjekt, auf der Basisebene aber ein Objekt. Die beiden Ebenen sind verknüpft über eine einzige Unterscheidung, doch B ist einmal Subjekt und sieht die Unterscheidung von aussen, doch gleichzeitig ist er auch ein Objekt dieser Unterscheidung, und wird dadurch als N oder S markiert. Das ist das Re-Entry. 

Das Re-Entry ist die logische Form der Paradoxie. Spencer-Browns Leistung besteht darin, dass er diese Form radikal einfach darstellt und sie formal maximal abstrahiert. Sie reduziert sich auf eine einzige Unterscheidung, die auf zwei Ebenen gelesen wird, einmal grundsätzlich (B ist N oder S) und dann als Re-Entry, wenn überlegt wird, ob B sich selber rasiert.

Das Paradox entsteht durch das Re-Entry plus eine Negation: Er rasiert die Männer, die sich nicht selber rasieren. Re-Entry und Negation gehört zwingend dazu, um ein echtes Paradox zu generieren. Sie lassen sich bei allen echten Paradoxien nachweisen, beim Barbierparadox, beim Lügnerparadox, beim Russelparadox usw.

Der Kern von jedem echten Paradox

Georg Spencer-Browns Leistung besteht darin, dass er das Paradox auf seinen essentiellen formalen Kern reduziert hat:

→ Eine (einzige) Unterscheidung mit Re-Entry und Negation.

Dieser Kern kann in jedem echten Paradox gefunden werden. Spencer-Brown’s Entdeckung von Unterscheidung und Re-Entry hat nun weitrechende Konsequenzen bezüglich Logik, aber auch weit über die Logik hinaus.

Darauf will ich gerne eingehen. Als nächstes möchte ich aber die Distinction, d.h. die Unterscheidung von Spencer-Brown als Logikelement mit einem anderen Logikelement vergleichen, das Ihnen sicher bestens bekannt ist, nämlich dem Bit.

Fortsetzung:  Unterscheidung (nach Spencer-Brown) und Bit

Frühere Beiträge zur Selbstreferenzialität und zum Re-Entry:

Selbstreferentialität 1

Selbstreferentialität 2 (Paradoxie)

Die Drei-Welten-Theorie (Roger Penrose)

Selbstreferentialität bringt klassische logische Systeme wie FOL oder Boolsche Algebra zum Absturz.

Mehr zum Thema Logik -> Übersichtsseite Logik

Information, Logik

Paradoxe Logikkerne (Teil 1)

Hinterlassen Sie einen Kommentar

Logik in Praxis und Theorie

Computerprogramme bestehen aus Algorithmen, d.h. aus Anweisungen, wie und in welcher Reihenfolge eine Eingabe zu bearbeiten ist. Algorithmen sind nichts anderes als angewandte Logik und ein Programmierer ist ein praktizierender Logiker.

Doch Logik ist ein weiter Begriff. Ganz eng gefasst, ist Logik ein Teil der Mathematik, ganz weit verstanden, ist Logik alles, was mit Denken zu tun hat. Diese beiden Pole zeigen einen deutlichen Kontrast: Die Logik der Mathematik ist geschlossen und wohldefiniert, die Logik des Denkens hingegen entzieht sich gern der präzisen Beobachtung: Wie komme ich auf einen bestimmten Gedanken? Wie verbinde ich meine Gedanken beim Denken? Und überhaupt: Was habe ich eben gedacht? Während die mathematische Logik mit klaren Begriffen und Regeln funktioniert, explizit und objektiv beschreibbar, ist die Logik des Denkens schwerer fassbar. Gibt es überhaupt Regeln des richtigen Denkens, so wie es in der mathematischen Logik Regeln dafür gibt, auf richtige Weise Schlüsse zu ziehen?

Wenn ich in diesen Unterschied zwischen mathematischer Logik und der Logik des Denkens eintauche, dann fällt mir etwas sofort auf: Das Nachdenken über mein Denken entzieht sich der Objektivität. Das ist bei der Mathematik nicht so. Mathematiker versuchen jeden kleinsten Denkschritt abzusichern, auf eine Weise, die klar und objektiv und für jeden nachvollziehbar, sobald er die mathematische Sprache versteht, ganz unabhängig von seiner Person: Das Subjekt des Mathematiker bleibt draussen.

Ganz anders ist es beim Denken. Wenn ich versuche, einen Gedanken zu beschreiben, den ich im Kopf habe, ist das mein persönlicher Gedanken, ein subjektives Geschehen, das sich primär nur meinem eigenen Denken zeigt und durch Wörter oder mathematische Formeln nur beschränkt ausgedrückt werden kann.

Doch genau dieser Widerstand reizt mich. Schliesslich möchte ich ‹korrekt› denken, und dazu ist es verlockend, zu verstehen, wie korrektes Denken überhaupt funktioniert.

Ich könnte nun Regress nehmen auf die mathematische Logik. Doch das Gehirn funktioniert nicht auf diese Weise. Auf welche Weise denn? Damit habe ich mich über viele Jahrzehnte beschäftigt, in der Praxis, ganz konkret bei dem Versuch, dem Computer NLP (Natural Language Processing) beizubringen, also explizite, maschinenfassbare Regeln zu finden für das Verstehen von Texten, ein Verstehen, das eigentlich ein subjektiver und zudem schwierig zu beschreibender Vorgang ist.

Meine Computerprogramme waren erfolgreich, doch das wirklich Interessante sind die Erkenntnisse, die ich dabei über das Denken gewinnen konnte, genauer, über die Logik, mit der wir denken.

Bei meiner Arbeit gelangen mir Erkenntnisse über den semantischen Raum, in dem wir denken, die Begriffe, die sich in diesem Raum aufhalten und die Art, wie sie sich bewegen. Doch die wichtigste Erkenntnis betraf die Zeit in der Logik. Darauf möchte ich jetzt eintreten.

Echte Paradoxe

Jeder, der sich ernsthaft mit Logik beschäftigt, ob professionell oder aus persönlichem Interesse, stösst früher oder später auf Paradoxe. Ein klassisches Paradox ist z.B. das Barbier-Paradox:

Das Barbierparadox

Der Barbier eines Dorfes wird dadurch definiert, dass er alle Männer rasiert, die sich nicht selber rasieren. Rasiert der Barbier sich selber? Wenn er das tut, gehört er zu den Männern, die sich selber rasieren und die er deshalb nicht rasiert. Wenn er sich somit nicht selber rasiert, gehört er aber zu den Männern, die er rasiert, also rasiert er auch sich selber. Dadurch gehört er aber zu den Männern, die er nicht rasieren muss. Also rasiert er sich nicht – usw. Das ist das Paradox: Wenn er sich rasiert, rasiert er sich nicht. Wenn er sich nicht rasiert, rasiert er sich.

Das gleiche Muster findet sich in weiteren Paradoxien, wie dem Lügnerparadox und vielen anderen. Man könnte nun denken, dass diese Art Paradoxien sehr gesucht sind und real keine Rolle spielen. Doch die Paradoxien spielen schon eine Rolle, zumindest an zwei Orten: in der Mathematik und im Denkvorgang.

Das Russel’sche Paradox und die Unvollständigkeitssätze von Kurt Gödel

Das Russel’sche Paradox hat das ‹Loch› in der Mengenlehre gezeigt. Die «Menge aller Mengen, die sich nicht selbst als Element enthalten» folgt dem gleichen Muster wie der Barbier des Barbierparadoxes und führt zur gleichen Art von unlösbarem Paradox. Etwas komplexer sind die beiden Unvollständigkeitssätze von Kurt Gödel, die aber letztlich auf dem gleichen Muster beruhen. Sowohl Russels wie Gödels Paradoxien sind für die Mathematik folgenreich. Das Russel Paradox hat dazu geführt, dass die Mengenlehre nicht mehr allein mit Mengen gebildet werden kann, weil das zu unhaltbaren Widersprüchen führt. Zermelo hatte deshalb die Mengen mit Klassen ergänzt und so die Geschlossenheit der Mengenlehre aufgeben müssen.

Auch Gödels Unvollständigkeitssätze beruhen letztlich auf dem gleichen Muster wie das Barbierparadox. Gödel hatte gezeigt, dass jedes formale System (formal im Sinn der Mathematik) Aussagen enthalten muss, die man formal weder beweisen noch widerlegen kann. Ein harter Schlag für die Mathematik und ihre formale Logik.

Spencer-Brown und die «Laws of Form»

Russels Widerlegung des simplen Mengenbegriffs und Gödels Beweis der Unvollständigkeit formaler Logik legen es nahe, näher über Paradoxe nachzudenken. Was ist das genau für ein logisches Muster, das hinter Russels und Gödels Problemen steckt? Was macht die Mengenlehre und die formale Logik unvollständig?

Die Frage hat mich lange beschäftigt. Überraschend hat es sich dann gezeigt, dass Paradoxien nicht nur lästige Übel sind, sondern dass es sich lohnt, sie vielmehr als sinnvolle Elemente in einer neuen formalen Logik einzusetzen. Dieser Schritt wurde vom Mathematiker Georg Spencer-Brown in seinem Buch «Laws of Form» von 1969 aufgezeigt, samt einem maximal einfachen Formalismus für Logik.

Ich möchte nun näher auf die Struktur der Paradoxien eintreten, wie sie Spencer-Browns aufgezeigt hat und auf die Konsequenzen, die sich daraus auf die Logik, die Physik, die Biologie und vieles mehr ergeben.

Fortsetzung: Paradoxe Logikkerne (Teil 2)

Logik

Selbstreferentialität 2 (Paradoxie)

Hinterlassen Sie einen Kommentar

(Fortsetzung von „Selbstreferentialität 1“)

Anweisung zur Generierung von Paradoxien

Der Trick mit dem sich klassische logische Systeme sprengen lassen besteht aus zwei Anweisungen:

1: Eine Aussage beziehe sich auf sich selber.
2: Im Bezug oder in der Aussage gibt es eine Verneinung.

Durch diese Konstellation entsteht immer eine Paradoxie.

Ein berühmtes Beispiel dafür ist der Barbier, der alle Männer des Dorfes rasiert, ausser natürlich diejenigen, die sich selber rasieren (die haben es ja nicht nötig). Die formale Paradoxie entsteht durch die Frage, ob dieser Barbier sich selber rasiert. Falls er es tut, gehört er zu den Männern, die sich selber rasieren, und diese rasiert er wie gesagt nicht. Also rasiert er sich nicht. Somit gehört er zu den Männern, die sich nicht selber rasieren – und diese rasiert er.

Auf diese Weise wechselt der Wahrheitsgehalt der Aussage, ob er sich selber rasiert, dauernd zwischen WAHR und FALSCH hin und hier. Diese Oszillation ist typisch für alle echten Paradoxien, so z.B. auch für den lügenden Kreter oder den formalen Beweis in Gödels Unvollständigkeitssatz, auch dort oszilliert der Wahrheitsgehalt einer Aussage kontinuierlich zwischen wahr und falsch und ist somit nicht entscheidbar. Im Barbierbeispiel sind neben der typischen Oszillation auch klar die oben erwähnten beiden Bedingungen für die echte Paradoxie erkennbar:

1. Selbstreferentialität: Rasiert er SICH SELBER?
2. Verneinung: Er rasiert sich selber rasierende Männer NICHT.

An dieser Stelle kann auf Spencer-Brown verwiesen werden, der einen Kalkül entwickelt hat, mit dem sich diese Verhältnisse klar zeigen lassen. Der Kalkül wird in seinem Text „Laws of Form“ dargestellt. Wer sich dafür interessiert, dem sei das Buch „Die Form der Paradoxie“ von Felix Lau empfohlen, das nicht nur den Kalkül für uns Laien nachvollziehbar macht, sondern sich auch sehr intensiv mit den Konsequenzen dieser Art Paradoxie beschäftigt.

Unechte Paradoxien

Diesen „klassischen“ Paradoxien möchte die „unechten“ Paradoxien gegenüberstellen, z.B. die „Paradoxie“ von Achilles und der Schildkröte. Hier handelt es sich nicht um echtes logisches Problem wie beim Barbier, sondern um den Fehler eines inadäquat gewählten Modells. Die Zeiten und Strecken, die die beiden Konkurrenten rennen, werden nämlich immer kürzer und nähern sich einem Wert, der innerhalb des gewählten Modells nicht überschritten werden kann. Somit kann Achilles die Schildkröte im Modell nicht überholen. In der Realität besteht aber kein Grund, dass die Zeiten und Strecken derart verzerrt und nicht linear betrachtet werden.

Die Unmöglichkeit zu überholen, besteht nur im Modell, das auf eine raffinierte Weise falsch gewählt ist. Ein Messsystem, das auf diese Weise verfälscht, ist natürlich nicht zulässig. Es handelt sich in Wirklichkeit nur um eine perfide Modellwahl, nicht um eine wirkliche Paradoxie. Entsprechend sind die beiden Kriterien für echte Paradoxa auch nicht vorhanden.

Modellwahl

Das Beispiel von Achilles und der Schildkröte zeigt die Bedeutung der korrekten Modellwahl. Die Modellwahl findet stets ausserhalb der Darstellung der Lösung statt und ist nicht Gegenstand eines logischen Beweises. Die Modellwahl hat vielmehr mit dem Bezug der Logik zur Realität zu tun. Sie findet auf einer übergeordneten Metaebene statt.

Mein Postulat ist es nun, dass zum Gebiet der Logik unbedingt auch die Modellwahl und nicht nur das Kalkül innerhalb des Modells gehört. Wie wählen wir ein Modell? Wenn Logik die Lehre vom richtigen Denken ist, dann muss diese Frage von der Logik mit behandelt werden.

Rolle der Metaebene für Modellwahl und Paradoxie

Das Zusammenwirken von zwei Ebenen, nämlich einer betrachteten Ebene und einer übergeordneten, betrachtenden Metaebene spielt nicht nur bei der Modellwahl, welche stets auf der Metaebene stattfindet, eine Rolle, sondern auch in der Form der echten Paradoxie. Die Selbstreferentialität in der echten Paradoxie führt nämlich unweigerliche die beiden Ebenen ein.

Eine Aussage, die sich auf sich selber bezieht, existiert zweimal, einmal auf der betrachteten Ebene, auf der sie quasi das „Objekt“ ist, das andere Mal auf der Metaebene, auf der sie sich auf sich selber bezieht. Die Oszillation der Paradoxie entsteht durch einen „Loop“, d.h. durch einen Kreisprozess zwischen den beiden Ebenen, dem das logische System nicht entrinnen kann.

Oszillierender Loop der Paradoxie, Selbstreferentialität und „Metasprung“

Es gibt übrigens zwei Arten solcher Loops, wie Felix Lau in seinem Buch aufzeigt: – eine negative (mit Verneinung), die zur Paradoxie führt – eine positive (mit Bestätigung), die zu einer Tautologie führt. Mit anderen Worten: Selbstreferentialität in logischen Systemen ist immer gefährlich! Es lohnt sich, zur Vermeidung, bzw. zur korrekten Behandlung von Paradoxien in logische Systeme den „Metasprung“ einzuführen – dieser ist der Bezug zwischen der betrachteten Ebene und der betrachtenden Metaebene.

Selbstreferentialität bringt klassische logische Systeme wie FOL oder Boolsche Algebra zum Absturz.

Mehr zum Thema Logik -> Übersichtsseite Logik