Begriffsmoleküle und NMR
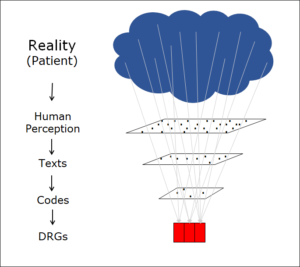
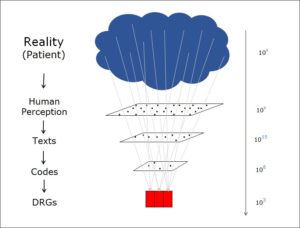
Im Beitrag Zwei Arten von Codierung 1 habe ich die Aufgabe beschrieben, Computer die beeindruckende Vielfalt der medizinischen Diagnosen «verstehen» zu lassen. Dazu war es nötig, die unterschiedlichen Diagnoseformulierungen beim Lesen durch den Computer in eine einheitliche Form zu überführen, welche alle semantischen Details in leicht abrufbarer Form repräsentiert.
Mit den Begriffsmolekülen ist uns das erfolgreich gelungen. Dabei halfen uns zwei Eigenschaften der Methode der Begriffsmoleküle, nämlich a) die konsequent komposite Repräsentation der Semantik, sowie b) ein Reasoner auf nicht-monotoner Basis. Die Verwendung eines nicht-monotonen Reasoners war damals überhaupt nicht im Trend. Die meisten Forschungsgruppen im Bereich der medizinischen Computerlinguistik waren gerade dabei, von der First-Order-Logic (FOL) auf Description Logic (DL) umzusteigen und glaubten, dass komplexe Semantiken am besten mit Hilfe von DL durch einen Computer interpretiert werden. In der Praxis allerdings zeigte sich, dass wir als kleine private Forschungsfirma ohne staatliche Unterstützung die erfolgreicheren waren. Wir setzten auf eine nicht-monotone Methode, während die anerkannte Lehrmeinung mit FOL und DL auf eine monotone Methode setzte.
Was ist monotone Logik?
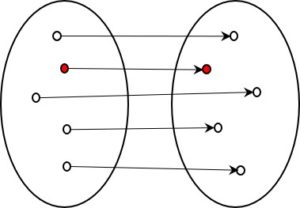
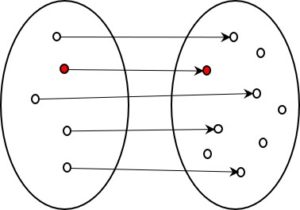
Monotonie bedeutet in der Logik, dass durch Schlüsse gewonnene Aussagen ihren Wahrheitsgehalt nicht ändern, auch wenn neue Aussagen dazu kommen, die ihnen widersprechen. Was also im System als wahr erkannt wurde, bleibt wahr, was als falsch erkannt wurde, bleibt falsch. Nicht-Monotonie bedeutet umgekehrt, dass durch das System gezogene Schlüsse auch wieder in Frage gestellt werden können.
Was ist das Problem bei der Nicht-Monotonie?
Man muss sich im Klaren sein, dass Beweise nur in einem monotonen System möglich sind. In einem nicht-monotonen weiss man nie, ob nicht irgendwoher ein Argument kommt, das zu ganz anderen Schlüssen führt. Da Beweise z.B. in der Mathematik essentiell sind, ist es einleuchtend, dass die mathematische Logik ganz klar auf Monotonie setzt.
Natürlich geht es bei der Computerlinguistik nicht um Beweise, sondern um korrekte Zuordnungen von Wörtern zu Begriffen. Der Vorteil, Beweise führen zu können, so wichtig er für die Mathematik ist, spielt für unsere Aufgabe keine Rolle.
Was ist das Problem bei der Monotonie?
Ein System, das seine Aussagen nicht verändern kann, ist nicht in der Lage, wirklich zu lernen. So funktioniert z.B. das menschliche Hirn mit Sicherheit nicht-monoton.
Ein monotones System muss auch geschlossen sein. In der Praxis sind wissenschaftliche Ontologien natürlich nicht geschlossen, sondern wachsen mit dem Erkenntnisfortschritt. Das gleiche Fortschreiten zeigt sich bei der Entwicklung eines Interpretationsprogramms. Auch hier gibt es eine kontinuierliche Verbesserung und Erweiterung, was monotone Systeme vor Probleme stellt.
Monotone Systeme können zudem mit Ausnahmen nicht so einfach umgehen. Jede Regel hat bekanntlich Ausnahmen und ein nicht-monotones System kann damit wesentlich gezielter und einfacher umgehen.
Nicht-Monotonie in der Praxis
Wenn man regelbasierte Systeme vergleicht, sind m.E. für unsere Aufgaben nicht-monotone den monotonen eindeutig vorzuziehen. Zwar ist die Nicht-Monotonie kein leichtes Pflaster und weist einige Fallen und Knacknüsse auf, doch die einfache Modellierbarkeit auch von detailreichen und komplexen Gebieten spricht für das nicht-monotone Reasoning.
Nicht-Monotonie ist eine Eigenschaft von dynamischen Logiken. Mehr zum Thema Logik -> Übersichtsseite Logik