Schlagwort-Archive: NLP

Information, Logik

Die Unterscheidung (nach Spencer-Brown) und das Bit

Hinterlassen Sie einen Kommentar

Fortsetzung von Paradoxe Logikkerne (2)

Geschichte

Bevor wir die Konsequenzen der Distinction von Georg Spencer-Brown (GSB) auf Logik, Physik, Biologie und Philosophie ansehen, ist es hilfreich, sie mit einer anderen, viel bekannteren Grundform zu vergleichen, nämlich dem Bit. Das ermöglich uns, die Natur von GSB’s distinction und das Revolutionäre seiner Innovation besser zu verstehen.

Bits und Forms können beide als Basis-Bausteine für die Informationsverarbeitung angesehen werden. Software-Strukturen bauen technisch auf Bits auf, doch die Forms von GSB («draw a distinction») sind genauso einfach, grundlegend und dabei verblüffend ähnlich. Trotzdem gibt es charakteristische Unterschiede.

     

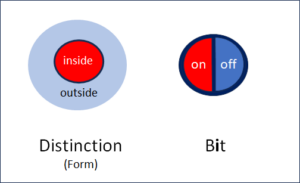
Abb. 1: Form und Bit zeigen Ähnlichkeit und Unterschiede

Sowohl Bit wie die Spencer-Brown Form sind in der Frühphase der Informatik entstanden, also relativ neue Vorstellung. Das Bit wurde von C.A. Shannon 1948 beschrieben, die Distinction von Georg Spencer-Brown (GSB) in seinem Buch «Laws of Form» im Jahr 1969, also nur ca. 20 Jahre später. 1969 fiel in die hohe Zeit der Hippie-Bewegung und GSB wurde in der Tat in Kaliforniens Hippie-Hochburg Esalen hoch willkommen geheissen. Das hat möglicherweise ein schlechtes Licht auf ihn geworfen und den etablierten Wissenschaftsbetrieb von ihm abgehalten. Während das Bit Kaliforniens entstehende Informations-High-Tech-Bewegung beflügelte, wurde Spencer-Browns mathematisch-logische Revolution von der Scientific Community geflissentlich ignoriert. Es ist Zeit, diesen Misstand zu überwinden.

Gemeinsamkeiten von Distinction und Bit

Beide, die Form und das Bit, beziehen sich auf Information. Beide sind elementare Abstraktionen und können deshalb als Grundbausteine von Information gesehen werden.

Diese Gemeinsamkeit zeigt sich darin, dass beide einen einzigen Aktionschritt bezeichnen – wenn auch einen unterschiedlichen – und beide dieser Aktion eine maximal reduzierte Anzahl von Ergebnissen zuordnen, nämlich genau zwei.

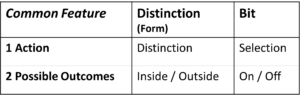
Tabelle 1: Sowohl Bit wie Distinction beinhalten
je eine Aktion und zwei mögliche Resultate (Outcomes)

Genau eine Aktion, genau zwei potentielle Ergebnisse

Die Aktion der Distinction ist die Distinction, also die Unterscheidung, die Aktion des Bits ist die Auswahl, also die Selection. Beide Aktionen sind als Informationshandlungen zu sehen und als solche fundamental, d.h. nicht weiter reduzierbar. Das Bit enthält in sich nicht weitere Bits, die Distinktion enthält in sich nicht weitere Distinktionen. Natürlich gibt es in der Umgebung des Bits weitere Bits und in der Umgebung einer Distinktion weitere Distinktionen. Beide Aktionen sind aber als fundamentale Informationshandlungen zu sehen. Ihre Fundamentalität wird unterstrichen durch die kleinst mögliche Zahl ihrer Ergebnisse, nämlich zwei. Die Zahl der Ergebnisse kann nicht kleiner sein, denn eine Unterscheidung von 1 ist keine Unterscheidung und eine Selektion aus 1 ist keine Selektion. Beides ist erst möglich, wenn es zwei potentielle Ergebnisse gibt.

Sowohl Distinction wie Bit sind somit unteilbare Informationshandlungen von radikaler, nicht zu steigernder Simplizität.

Trotzdem sind sie nicht gleich und auch nicht austauschbar. Sie ergänzen sich.

Während das Bit seit 1948 einen technischen Höhenflug angetreten ist, ist seine Voraussetzung, die Unterscheidung (distinction), ungenannt im Hintergrund geblieben. Umso mehr lohnt es sich, sie heute in den Vordergrund zu rücken und so ein neues Licht auf die Grundlagen von Mathematik, Logik, Natur- und Geisteswissenschaften zu werfen.

Unterschiede

Informationsgehalt und die Entropie nach Shannon

Beide, Form und Bit, beziehen sich auf Information. In der Physik wird der quantitative Gehalt an Information als Entropie bezeichnet.

Der Informationsgehalt, wenn ein Bit gesetzt, bzw. eine Unterscheidung getroffen wird, ist auf den ersten Blick in beiden Fällen gleich gross, nämlich die Information, die zwischen zwei Zuständen unterscheidet. Das ist beim Bit ganz klar so. Sein Informationsgehalt ist, wie Shannon gezeigt hat, log2(2) = 1. Shannon hat diesen dimensionslosen Wert als 1 Bit bezeichnet. Das Bit enthält somit – nicht ganz überraschend – die Information von einem Bit. So ist es von Shannon definiert worden.

Das Bit und die Entropie

Das Bit misst nichts anderes als die Entropie. Der Begriff Entropie stammt ursprünglich aus der Wärmelehre und dient dazu, das Verhalten von Wärmemaschinen zu berechnen. Entropie ist der Partnerbegriff der Energie und gilt – wie der Begriff Energie – überall in der Physik, nicht nur in der Wärmelehre.

Was ist Entropie?

Die Entropie misst also – seit Shannon – den Informationsgehalt. Wenn ich etwas nicht weiss und es anschliessend erfahre, fliesst Entropie als Information. Wenn – bevor ich weiss, was gilt – zwei Zustände möglich sind, dann erhalte ich, wenn ich erfahre, welcher der beiden Zustände zutrifft, eine Information mit dem quantitativen Wert 1 Bit.

Wenn mehr als zwei Zustände möglich sind, steigt die Zahl der Bits logarithmisch mit der Zahl der möglichen Zustände; so braucht es drei 2-er Wahlen um aus 8 Möglichkeiten die zutreffende herauszufinden, also genau drei Bits. Die Zahl der Wahlen (Bits) verhält sich zur Zahl der Auswahlmöglichkeiten wie das Beispiel zeigt, logarithmisch.

Zweierwahl = 1 Bit = log2(2).
Viererwahl = 2 Bit = log2(4)
Achterwahl = 3 Bit = log2(8)

Der Informationsgehalt eines einzigen Bits ist stets der Informationsgehalt einer einzigen Zweierwahl, also log2(2) = 1. Das Bit als physikalische Grösse ist dimensionslos, also eine reine Zahl. Das passt, weil die Information über die Wahl neutral ist, und nicht etwa eine Länge, ein Gewicht, eine Energie oder eine Temperatur. So viel zum Bit, der technischen Einheit der des quantitativen Informationsgehaltes. Wie verhält es sich nun bei der anderen Grundeinheit von Information, der Form von Spencer-Brown?

Der Informationsgehalt der Form

Der Informationsgehalt des Bits ist genau 1, wenn die beiden Outcomes der Selektion genau gleich wahrscheinlich sind. Sobald von zwei Zuständen einer unwahrscheinlicher ist, ist die Information grösser, wenn er, trotz der geringeren Vorwahrscheinlichkeit, gewählt wird. Je unwahrscheinlicher er ist, umso grösser wird die Information, wenn die Wahl auf ihn fällt. Nur beim klassischen Bit ist die Wahrscheinlichkeit für beide Zustände per Definition gleich gross.

Das ist ganz anders bei der Form der Unterscheidung von Spencer-Brown. Das Entscheidende dabei ist der ‹unmarked space›. Die Distinktion unterscheidet etwas vom Rest und markiert es. Der Rest, also alles andere bleibt unmarkiert, Spencer-Brown nennt es den ‹unmarked space›.

Wir können und müssen nun davon ausgehen, dass der Rest, das Unmarkierte, viel grösser ist, und die Wahrscheinlichkeit seines Eintretens viel grösser ist, als die Wahrscheinlichkeit, dass das Markierte eintrifft. Der Informationsgehalt des Markierten ist deshalb immer grösser als 1.

Natürlich geht es bei der Unterscheidung um das Markierte. Deshalb wird für den Informationsgehalt der Unterscheidung das Markierte und nicht das Unmarkierte gerechnet. Wie gross ist nun der Raum des Unmarkierten? Wir tun gut daran, davon ausgehen, dass er unendlich ist. Ich kann nie wissen, was ich alles nicht weiss.

Der Unterschied im Informationsgehalt, gemessen als Entropie, ist der erste Unterschied zwischen Bit und Unterscheidung. Beim Bit ist der Informationsgehalt, d.h. die Entropie genau 1, bei der Unterscheidung kommt es darauf an, wie gross der Unmarkierte Raum gesehen wird, er ist aber stets grösser als der markierte und die Entropie der Unterscheidung ist deshalb aus mathematischen Gründen stets grösser als 1.

Geschlossenheit und Offenheit

Die Abb. 1 oben zeigt den wichtigsten Unterschied von Distinktion und Bit, nämlich ihre Grenzen gegen aussen. Diese ist beim Bit klar definiert.

Die Bedeutungen im einem Bit

Das Bit enthält zwei Zustände, von denen einer aktiviert ist, der andere nicht. Ausser diesen beiden Zuständen ist nichts im Bit zu sehen und alle andere Information befindet sich ausserhalb des Bits. Nicht einmal die Bedeutungen der beiden Zustände sind definiert. Sie können 0 und 1, Wahr undd Falsch, Positiv und Negativ oder jedes andere Paar bedeuten, das sich gegenseitig ausschliesst. Das Bit selber enthält diese Bedeutungen nicht, nur die Information, welcher der beiden Zustände gewählt wurde. Die Bedeutung der beiden Zuständen wird ausserhalb des Bits geregelt und von ausserhalb zugewiesen. Diese Neutralität des Bits ist seine Stärke. Es kann jede Bedeutung annehmen und ist deshalb überall einsetzbar, wo Information technisch prozessiert wird.

Die Bedeutung in einer Unterscheidung

Ganz anders ist das bei der Unterscheidung. Hier wird die Bedeutung markiert. Dazu wird das Innere der Unterscheidung vom Äusseren unterschieden. Das Äussere aber ist offen und es gibt nichts, was nicht dazu gehört. Der ‹unmarked space› ist im Prinzip unendlich. Eine Grenze wird definiert, doch sie ist die Unterscheidung selber. Deshalb kann sich die Unterscheidung nicht wirklich gegen aussen abgrenzen, im Gegensatz zum Bit.

Mit anderen Worten:

→  Das Bit ist geschlossen, die Unterscheidung nicht.

Unterschiede zwischen Unterscheidung und Bit


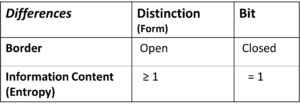
Tabelle 2: Unterschiede ziwschen Distinction (Form) und Bit

Die Unterschiede haben nun einige interessante Konsequenzen.

Konsequenzen

Bits und Offenheit in einer Software (Beispiel NLP)

Das Bit hat durch seine definierte und simple Entropie den technologischen Vorteil der einfachen Handhabbarkeit, was wir uns in der Software-Industrie zu Nutze machen. Die Forms hingegen sind durch ihre Offenheit realitätsgerechter. Für unsere konkrete Aufgabe der Interpretation von medizinischen Texten stiessen wir deshalb auf die Notwendigket, die Offenheit auch in der Bitwelt der technischen Software durch bestimmte Prinzipien einzuführen. Stichworte dazu sind:

  1. Einführung eines handelnden Subjekts, das den Input nach eigenen Internen Regeln bewertet,
  2. Arbeiten mit wechselnden Ontologien und Klassifikationen,
  3. Abkehr von der klassischen, d.h. statischen und monotonen Logik zu einer nicht-monotonen Logik,
  4. Integration der Zeit als Logikelement (nicht nur als Variable).

Mehr zum Thema Information -> Übersichtsseite Informationstheorie

 

Information, Logik

Paradoxe Logikkerne (Teil 1)

Hinterlassen Sie einen Kommentar

Logik in Praxis und Theorie

Computerprogramme bestehen aus Algorithmen, d.h. aus Anweisungen, wie und in welcher Reihenfolge eine Eingabe zu bearbeiten ist. Algorithmen sind nichts anderes als angewandte Logik und ein Programmierer ist ein praktizierender Logiker.

Doch Logik ist ein weiter Begriff. Ganz eng gefasst, ist Logik ein Teil der Mathematik, ganz weit verstanden, ist Logik alles, was mit Denken zu tun hat. Diese beiden Pole zeigen einen deutlichen Kontrast: Die Logik der Mathematik ist geschlossen und wohldefiniert, die Logik des Denkens hingegen entzieht sich gern der präzisen Beobachtung: Wie komme ich auf einen bestimmten Gedanken? Wie verbinde ich meine Gedanken beim Denken? Und überhaupt: Was habe ich eben gedacht? Während die mathematische Logik mit klaren Begriffen und Regeln funktioniert, explizit und objektiv beschreibbar, ist die Logik des Denkens schwerer fassbar. Gibt es überhaupt Regeln des richtigen Denkens, so wie es in der mathematischen Logik Regeln dafür gibt, auf richtige Weise Schlüsse zu ziehen?

Wenn ich in diesen Unterschied zwischen mathematischer Logik und der Logik des Denkens eintauche, dann fällt mir etwas sofort auf: Das Nachdenken über mein Denken entzieht sich der Objektivität. Das ist bei der Mathematik nicht so. Mathematiker versuchen jeden kleinsten Denkschritt abzusichern, auf eine Weise, die klar und objektiv und für jeden nachvollziehbar, sobald er die mathematische Sprache versteht, ganz unabhängig von seiner Person: Das Subjekt des Mathematiker bleibt draussen.

Ganz anders ist es beim Denken. Wenn ich versuche, einen Gedanken zu beschreiben, den ich im Kopf habe, ist das mein persönlicher Gedanken, ein subjektives Geschehen, das sich primär nur meinem eigenen Denken zeigt und durch Wörter oder mathematische Formeln nur beschränkt ausgedrückt werden kann.

Doch genau dieser Widerstand reizt mich. Schliesslich möchte ich ‹korrekt› denken, und dazu ist es verlockend, zu verstehen, wie korrektes Denken überhaupt funktioniert.

Ich könnte nun Regress nehmen auf die mathematische Logik. Doch das Gehirn funktioniert nicht auf diese Weise. Auf welche Weise denn? Damit habe ich mich über viele Jahrzehnte beschäftigt, in der Praxis, ganz konkret bei dem Versuch, dem Computer NLP (Natural Language Processing) beizubringen, also explizite, maschinenfassbare Regeln zu finden für das Verstehen von Texten, ein Verstehen, das eigentlich ein subjektiver und zudem schwierig zu beschreibender Vorgang ist.

Meine Computerprogramme waren erfolgreich, doch das wirklich Interessante sind die Erkenntnisse, die ich dabei über das Denken gewinnen konnte, genauer, über die Logik, mit der wir denken.

Bei meiner Arbeit gelangen mir Erkenntnisse über den semantischen Raum, in dem wir denken, die Begriffe, die sich in diesem Raum aufhalten und die Art, wie sie sich bewegen. Doch die wichtigste Erkenntnis betraf die Zeit in der Logik. Darauf möchte ich jetzt eintreten.

Echte Paradoxe

Jeder, der sich ernsthaft mit Logik beschäftigt, ob professionell oder aus persönlichem Interesse, stösst früher oder später auf Paradoxe. Ein klassisches Paradox ist z.B. das Barbier-Paradox:

Das Barbierparadox

Der Barbier eines Dorfes wird dadurch definiert, dass er alle Männer rasiert, die sich nicht selber rasieren. Rasiert der Barbier sich selber? Wenn er das tut, gehört er zu den Männern, die sich selber rasieren und die er deshalb nicht rasiert. Wenn er sich somit nicht selber rasiert, gehört er aber zu den Männern, die er rasiert, also rasiert er auch sich selber. Dadurch gehört er aber zu den Männern, die er nicht rasieren muss. Also rasiert er sich nicht – usw. Das ist das Paradox: Wenn er sich rasiert, rasiert er sich nicht. Wenn er sich nicht rasiert, rasiert er sich.

Das gleiche Muster findet sich in weiteren Paradoxien, wie dem Lügnerparadox und vielen anderen. Man könnte nun denken, dass diese Art Paradoxien sehr gesucht sind und real keine Rolle spielen. Doch die Paradoxien spielen schon eine Rolle, zumindest an zwei Orten: in der Mathematik und im Denkvorgang.

Das Russel’sche Paradox und die Unvollständigkeitssätze von Kurt Gödel

Das Russel’sche Paradox hat das ‹Loch› in der Mengenlehre gezeigt. Die «Menge aller Mengen, die sich nicht selbst als Element enthalten» folgt dem gleichen Muster wie der Barbier des Barbierparadoxes und führt zur gleichen Art von unlösbarem Paradox. Etwas komplexer sind die beiden Unvollständigkeitssätze von Kurt Gödel, die aber letztlich auf dem gleichen Muster beruhen. Sowohl Russels wie Gödels Paradoxien sind für die Mathematik folgenreich. Das Russel Paradox hat dazu geführt, dass die Mengenlehre nicht mehr allein mit Mengen gebildet werden kann, weil das zu unhaltbaren Widersprüchen führt. Zermelo hatte deshalb die Mengen mit Klassen ergänzt und so die Geschlossenheit der Mengenlehre aufgeben müssen.

Auch Gödels Unvollständigkeitssätze beruhen letztlich auf dem gleichen Muster wie das Barbierparadox. Gödel hatte gezeigt, dass jedes formale System (formal im Sinn der Mathematik) Aussagen enthalten muss, die man formal weder beweisen noch widerlegen kann. Ein harter Schlag für die Mathematik und ihre formale Logik.

Spencer-Brown und die «Laws of Form»

Russels Widerlegung des simplen Mengenbegriffs und Gödels Beweis der Unvollständigkeit formaler Logik legen es nahe, näher über Paradoxe nachzudenken. Was ist das genau für ein logisches Muster, das hinter Russels und Gödels Problemen steckt? Was macht die Mengenlehre und die formale Logik unvollständig?

Die Frage hat mich lange beschäftigt. Überraschend hat es sich dann gezeigt, dass Paradoxien nicht nur lästige Übel sind, sondern dass es sich lohnt, sie vielmehr als sinnvolle Elemente in einer neuen formalen Logik einzusetzen. Dieser Schritt wurde vom Mathematiker Georg Spencer-Brown in seinem Buch «Laws of Form» von 1969 aufgezeigt, samt einem maximal einfachen Formalismus für Logik.

Ich möchte nun näher auf die Struktur der Paradoxien eintreten, wie sie Spencer-Browns aufgezeigt hat und auf die Konsequenzen, die sich daraus auf die Logik, die Physik, die Biologie und vieles mehr ergeben.

Fortsetzung: Paradoxe Logikkerne (Teil 2)

Künstliche Intelligenz

Aktuelle Pressetexte zur Künstlichen Intelligenz

Hinterlassen Sie einen Kommentar

Meine These, dass sogenannte KI-Programme zwar ausserordentlich leistungsfähig sind, doch ihre Intelligenz bestenfalls geborgt haben und zu eigenständigen Denkleistungen aus prinzipiellen Gründen nicht imstande sind, wird zunehmend auch von anderen Seiten unterstützt.

Hier drei Publikationen mit dieser Stossrichtung:

  1. St. Galler Tagblatt, 3. August 2021, Christoph Bopp: «Dr. Frankenstein verwirrte die Künstliche Intelligenz«:
    https://www.tagblatt.ch/leben/ki-uund-medizin-doktor-frankenstein-verwirrte-die-kuenstliche-intelligenz-ld.2169958
    .
  2. The Gradient: 3. August 2021, Valid S. Saba: «Machine Learning Won’t Solve Natual Language Understanding«:
    https://thegradient.pub/machine-learning-wont-solve-the-natural-language-understanding-challenge/
    .
  3. Neue Zürcher Zeitung, 17. August 2021, Adrian Lobe: «Man kann Algorithmen zu Kommunisten erziehen, aber sie können auch zu Rassisten werden, wenn sie in schlechte Gesellschaft geraten»
    https://www.nzz.ch/feuilleton/wie-die-black-box-lernt-bots-kann-man-zu-rassisten-machen-ld.1636315?ga=1&kid=nl165_2021-8-16&mktcid=nled&mktcval=165_2021-
    08-17

Diese Texte zeigen beispielhaft,

  •  wie der Lern-Korpus das Ergebnis der KI bestimmt (NZZ über den chinesischen Chatbot):
    Bei Neuronalen Netzen gilt bekanntlich: «Garbage In, Garbage Out» – der Korpus bestimmt was überhaupt erkennbar ist und was «wahr» ist, die KI kann nur ausgeben, was der Korpus vorgibt.
  • wie komplexe Sachverhalte in einem noch unklaren Kontext für KI-Systeme schlecht durchschaubar sind (Tagblatt über falsche Prognosen in der Covid-Epidemie):
    Bei komplexen Sachverhalten nimmt der Bedarf an Korpusdaten überproportional zu. Die rein technischen Probleme sind dabei noch die kleinsten.
  • wo die wirklichen Herausforderungen für NLP liegen (The Gradient über Natural Language):
    Dieser aktuelle Text aus den USA stellt die gleichen Thesen auf und verwendet gleiche Argumentationslinien wie ich z.B. in meinem Buch von 2001, dass nämlich die Semantik, also die Bedeutung eines Textes im Kopf verstanden werden muss – und genau das kann die KI der Neuronalen Netze eben nicht.

Die KI der Neuronalen Netze bleibt allerdings eine hochpotente, sinnvolle und hilfreiche Technologie – nur müssen wir wissen, was sie kann und was nicht.

Künstliche Intelligenz, Logik

Zur KI: Schnaps und Panzer

Hinterlassen Sie einen Kommentar
KI im letzten Jahrhundert

KI ist heute ein grosses Schlagwort, war aber bereits in den 80er und 90er Jahren des letzten Jahrhunderts ein Thema, das für mich auf meinem Gebiet des Natural Language Processing interessant war. Es gab damals zwei Methoden, die gelegentlich als KI bezeichnet wurden und die unterschiedlicher nicht hätten sein können. Das Spannende daran ist, dass diese beiden unterschiedlichen Methoden heute noch existieren und sich weiterhin essenziell voneinander unterscheiden.

KI-1: Schnaps

Die erste, d.h. die Methode, die bereits die allerersten Computerpioniere verwendeten, war eine rein algorithmische, d.h. eine regelbasierte. Beispielhaft für diese Art Regelsysteme sind die Syllogismen des Aristoteles:

Prämisse 1: Alle Menschen sind sterblich.
Prämisse 2: Sokrates ist ein Mensch.
Schlussfolgerung: Sokrates ist sterblich.

Der Experte gibt Prämisse 1 und 2 ein, und das System zieht dann selbstständig die Schlussfolgerung. Solche Systeme lassen sich mathematisch untermauern. Mengenlehre und First-Order-Logic (Aussagelogik ersten Grades) gelten oft als sichere mathematische Grundlage. Theoretisch waren diese Systeme somit wasserdicht abgesichert. In der Praxis sah die Geschichte allerdings etwas anders aus. Probleme ergaben sich durch die Tatsache, dass auch die kleinsten Details in das Regelsystem aufgenommen werden mussten, da sonst das Gesamtsystem «abstürzte», d.h. total abstruse Schlüsse zog. Die Korrektur dieser Details nahm mit der Grösse des abgedeckten Wissens überproportional zu. Die Systeme funktionierten allenfalls für kleine Spezialgebiete, für die klare Regeln gefunden werden konnten, für ausgedehntere Gebiete wurden die Regelbasen aber zu gross und waren nicht mehr wartbar. Ein weiteres gravierendes Problem war die Unschärfe, die vielen Ausdrücken eigen ist, und die mit solchen hart-kodierten Systemen schwer in den Griff zu bekommen ist.

Diese Art KI geriet also zunehmend in die Kritik. Kolportiert wurde z.B. folgender Übersetzungsversuch: Ein NLP-Programm übersetzte Sätze vom Englischen ins Russische und wieder zurück, dabei ergab die Eingabe:
«Das Fleisch ist willig, aber der Geist ist schwach» die Übersetzung:
«Das Steak ist kräftig, aber der Schnaps ist lahm.»

Die Geschichte hat sich vermutlich nicht genau so zugetragen, aber das Beispiel zeigt die Schwierigkeiten, wenn man versucht, Sprache mit regelbasierten Systemen einzufangen. Die Anfangseuphorie, die seit den 50er Jahren mit dem «Elektronenhirn» und seiner «maschinellen Intelligenz» verbunden worden war, verblasste, der Ausdruck «Künstliche Intelligenz» wurde obsolet und durch den Ausdruck «Expertensystem» ersetzt, der weniger hochgestochen klang.

Später, d.h. um 2000, gewannen die Anhänger der regelbasierten KI allerdings wieder Auftrieb. Tim Berners-Lee, Pionier des WWW, lancierte zur besseren Benutzbarkeit des Internets die Initiative Semantic Web. Die Experten der regelbasierten KI, ausgebildet an den besten technischen Hochschulen der Welt, waren gern bereit, ihm dafür Wissensbasen zu bauen, die sie nun Ontologien nannten. Bei allem Respekt vor Berners-Lee und seinem Bestreben, Semantik ins Netz zu bringen, muss festgestellt werden, dass die Initiative Semantic Web nach bald 20 Jahren das Internet nicht wesentlich verändert hat. Meines Erachtens gibt es gute Gründe dafür: Die Methoden der klassischen mathematischen Logik sind zu rigid, die komplexen Vorgänge des Denkens nachzuvollziehen – mehr dazu in meinen anderen Beiträgen, insbesondere zur statischen und dynamischen Logik. Jedenfalls haben weder die klassischen regelbasierten Expertensysteme des 20. Jahrhunderts noch die Initiative «Semantic Web» die hoch gesteckten Erwartungen erfüllt.

KI-2: Panzer

In den 90er Jahren gab es aber durchaus auch schon Alternativen, die versuchten, die Schwächen der rigiden Aussagenlogik zu korrigieren. Dazu wurde das mathematische Instrumentarium erweitert.

Ein solcher Versuch war die Fuzzy Logic. Eine Aussage oder eine Schlussfolgerung war nun nicht mehr eindeutig wahr oder falsch, sondern der Wahrheitsgehalt konnte gewichtet werden. Neben Mengenlehre und Prädikatenlogik hielt nun auch die Wahrscheinlichkeitstheorie Einzug ins mathematische Instrumentarium der Expertensysteme. Doch einige Probleme blieben: Wieder musste genau und aufwendig beschrieben werden, welche Regeln gelten. Die Fuzzy Logic gehört also ebenfalls zur regelbasierten KI, wenn auch mit Wahrscheinlichkeiten versehen. Heute funktionieren solche Programme in kleinen, wohlabgegrenzten technischen Nischen perfekt, haben aber darüberhinaus keine Bedeutung.

Eine andere Alternative waren damals die Neuronalen Netze. Sie galten als interessant, allerdings wurden ihre praktischen Anwendungen eher etwas belächelt. Folgende Geschichte wurde dazu herum

gereicht:

Die amerikanische Armee – seit jeher ein wesentlicher Treiber der Computertechnologie – soll ein neuronales Netz zur Erkennung von eigenen und fremden Panzern gebaut haben. Ein neuronales Netz funktioniert so, dass die Schlussfolgerungen über mehrere Schichten von Folgerungen vom System selber gefunden werden. Der Mensch muss also keine Regeln mehr eingeben, diese werden vom System selber erstellt.

Wie kann das System das? Es braucht dazu einen Lernkorpus. Bei der Panzererkennung war das eine Serie von Fotos von amerikanischen und russischen Panzern. Für jedes Foto war also bekannt, ob amerikanisch oder russisch, und das System wurde nun so lange trainiert, bis es die geforderten Zuordnungen selbstständig erstellten konnte. Die Experten nahmen auf das Programm nur indirekt Einfluss, indem sie den Lernkorpus aufbauten; das Programm stellte die Folgerungen im neuronalen Netz selbstständig zusammen – ohne dass die Experten genau wussten, aus welchen Details das System mit welchen Regeln welche Schlüsse zog. Nur das Resultat musste natürlich stimmen. Wenn das System nun den Lernkorpus vollkommen integriert hatte, konnte man es testen, indem man ihm einen neuen Input zeigte, z.B. ein neues Panzerfoto, und es wurde erwartet, dass es mit den aus dem Lernkorpus gefundenen Regeln das neue Bild korrekt zuordnete. Die Zuordnung geschah, wie gesagt, selbständig durch das System, ohne dass der Experte weiteren Einfluss nahm und ohne dass er genau wusste, wie im konkreten Fall die Schlüsse gezogen wurden.

Das funktionierte, so wurde erzählt, bei dem Panzererkennungsprogramm perfekt. So viele Fotos dem Programm auch gezeigt wurden, stets erfolgte die korrekte Zuordnung. Die Experten konnten selber kaum glauben, dass sie wirklich ein Programm mit einer hundertprozentigen Erkennungsrate erstellt hatten. Wie konnte so etwas sein? Schliesslich fanden sie den Grund: Die Fotos der amerikanischen Panzer waren in Farbe, diejenigen der russischen schwarzweiss. Das Programm musste also nur die Farbe erkennen, die Silhouetten der Panzer waren irrelevant.

Regelbasiert versus korpusbasiert

Die beiden Anekdoten zeigen, welche Probleme damals auf die regelbasierte und die korpusbasierte KI warteten.

  • Bei der regelbasierten KI waren es:
    – die Rigidität der mathematischen Logik
    – die Unschärfe unserer Wörter
    – die Notwendigkeit, sehr grosse Wissenbasen aufzubauen
    – die Notwendigkeit, Fachexperten für die Wissensbasen einzusetzen
  • Bei der korpusbasierten KI waren es:
    – die Intransparenz der Schlussfolgerungs-Wege
    – die Notwendigkeit, einen sehr grossen und relevanten Lernkorpus aufzubauen

Ich hoffe, dass ich mit den beiden oben beschriebenen, zugegebenermassen etwas unfairen Beispielen den Charakter und die Wirkweise der beiden KI-Typen habe darstellen können, mitsamt den Schwächen, die die beiden Typen jeweils kennzeichnen.

Die Herausforderungen bestehen selbstverständlich weiterhin.  In den folgenden Beiträgen werde ich darstellen, wie die beiden KI-Typen darauf reagiert haben und wo bei den beiden Systemen nun wirklich die Intelligenz sitzt. Als Erstes schauen wir die korpusbasierte KI an.

Dies ist ein Beitrag zum Thema künstliche Intelligenz.