Schlagwort-Archive: physikalische Welt

Drei-Welten-Theorie

Was ist Resonanz?

Hinterlassen Sie einen Kommentar

Die physikalische Basis der Resonanz

Resonanz basiert auf den Eigenschwingungen von physikalischen Medien und ihrer gegenseitigen Koppelung.

Koppelung der Eigenschwingungen von physikalischen Objekten

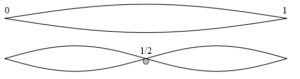
Die Eigenschwingungen sind stehende Wellen, deren Frequenz von den Eigenschaften des physikalischen Mediums (Grösse, Form, Material, etc. ) bestimmt wird.

Zwei solche Medien können über ihre Eigenschwingung in eine  Resonanz treten. Die Resonanz entsteht durch eine Koppelung der beiden Eigenschwingungen, sodass die beiden physikalischen Medien in ihrem Schwingungsverhalten eine gekoppelte Einheit bilden.

Die Koppelung erfolgt über einen physikalischen Energieaustausch, sei es direkt oder indirekt, z.B. über die Luft. Bedingung für das Entstehen der Koppelung ist, dass die Frequenzen der Eigenschwingungen der beiden beteiligten physikalischen Medien in einem dafür geeigneten mathematischen Verhältnis stehen.

Stabilität der Resonanz über die Zeit

Sobald der Resonanzzustand eingetreten ist, bleibt er eine gewisse Zeitspanne stabil, d.h. der gekoppelte Schwingungszustand bleibt stationär, oft über eine längere Zeit. Dieses erstaunliche Verhalten hat mit den Energieverhältnissen zu tun, die bei der Koppelung besonders energiegünstig sind.

Resonante Eigenschwingungen

Auch die Eigenschwingung eines einzelnen physikalischen Objekts kann als Resonanz bezeichnet werden. So weist z.B. ein Elektron um den Atomkern eine Resonanz mit sich selber auf und kann dadurch nur ganz bestimmte Umlauffrequenzen annehmen, die es ihm erlauben, auf seiner Umlaufbahn mit sich selber resonant zu sein. Das Gleiche gilt für das Schwingungsverhalten einer Saite.

Resonanz als Abstraktion

Das physikalische Material bestimmt zwar die Eigenfrequenz der beteiligten schwingenden Medien, doch der Rest, d.h. das Entstehen der gekoppelten Resonanz, ergibt sich aus dem geeigneten Verhältnis der beiden Frequenzen. Dieses Frequenzverhältnis folgt mathematischen Regeln. Eine verblüffend einfache Mathematik reicht aus, zu erkennen, wie stark die Resonanz zwischen den beiden schwingenden physikalischen Medien sein wird.

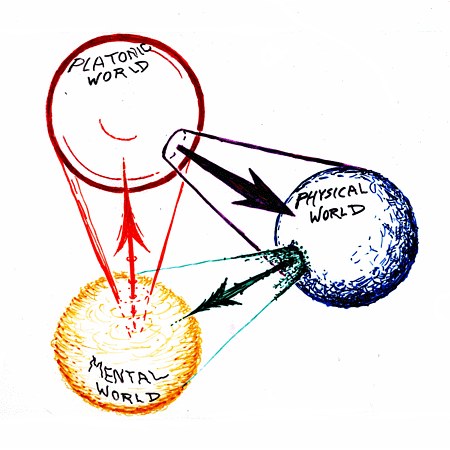
Drei Welten, nach Roger Penrose

Die Entstehung der Resonanz zeigt eindrücklich das Zusammenspiel von zwei der drei Welten, die gemäss Nobelpreisträger Roger Penrose unsere Realität bilden, nämlich der physikalischen und der platonischen. Letzerer Begriff bezeichnet die abstrakte Welt der Ideen, zu der die Mathematik gehört. Mit der Verwendung des Begriffs ‹platonisch› für die Welt der Mathematik verweist Sir Roger auf die europäische Kulturgeschichte, hier gehört die Diskussion um die Wirklichkeit und Wirksamkeit von Ideen nicht nur zur Philosophie von Platon, sondern bestimmte auch im Mittelalter als Universaliendisput grosse Teile des philosophischen Diskurses. Die Frage hat seither nichts an Relevanz verloren: Wie real sind Ideen? Warum setzt sich Abstraktes in der materiellen Welt durch? Wie ist das Verhältnis von abstrakter Idee und konkreter, d.h. physikalischer Welt?

Ich dachte vor gut einem Jahr, dass das Entstehen der Resonanz in der Musik ein gutes Beispiel wäre, um das Verhältnis von Physik, Mathematik und der dritten Welt, unserem subjektiven Empfinden zu erkunden. Ich war überrascht, wie verblüffend klar der Bezug der drei Welten hier dargestellt werden kann und wie verblüffend einfach, logisch und weitreichend die Mathematik in den Harmonien unserer Musik ist.

Resonanz in der Musik

In einem Musikstück ändern die entstehenden Resonanzen zwischen den Tönen immer wieder und bieten so einen faszinierenden Farbwechsel. Wir können ihn intuitiv erleben, aber auch rational erklären, eben als ein Spiel der Resonanzen unter den Tönen.

Nur die Obertonreihe?

In der Schule habe ich gelernt, dass die Obertonreihe unsere Tonleitern bestimmt. Doch das ist eine grobe Vereinfachung. Das Phänomen der Resonanz kann unsere Tonleitern viel einfacher und direkter erklären als es die Obertonreihe kann. Die Obertonreihe beschreibt das Schwingungsverhalten nämlich nur innerhalb eines physikalischen Medium – die in der Musik interessierende Resonanz entsteht jedoch immer zwischen mindestens zwei verschiedenen Medien (Tönen). Für die Resonanzüberlegungen von zwei Tönen müssen wir konsequenterweise auch zwei Obertonreihen vergleichen. Erst das Nebeneinanderlegen der beiden Reihen erklärt das Geschehen – ein Fakt, der in den Lehrbüchern meist übergangen wird.

Akkorde bestehen aus drei oder mehr Tönen. Auch hier kann die Resonanzanalyse der drei oder mehr beteiligten Töne die Akkordwirkung verblüffend einfach erklären. Nur müssen diesmal nicht die Frequenzen von zwei, sondern von mehreren Tönen gleichzeitig berücksichtigt werden.

Reine und temperierte Stimmung

In Europa hat sich im Barock die gleichmässig temperierte Stimmung durchgesetzt, welche die kompositorischen Möglichkeiten vielfältig erweitert. Das erste, was der Laie zur Theorie der Tonleitern findet, ist deshalb eine genaue Beschreibung der Abweichungen der temperierten von der reinen Stimmung – doch diese Abweichungen sind für die Entstehung von Resonanzen nur von marginaler Bedeutung. Die reine Stimmung ist keine Bedingung für Resonanz, die hier vorgestellte Mathematik der Resonanz erklärt das Phänomen präzis auch bei temperierter Stimmung.

Dies ist ein Beitrag zur Drei-Welten-Theorie nach Penrose und der Herkunft der Tonleitern.

Drei-Welten-Theorie, Information

Resonanz und Oktave

2 Kommentare

Dies ist ein Beitrag zur Entstehung der Tonleitern und setzt den Beitrag zur Oktave fort.

Wir erzeugen eine Resonanz

Falls Resonanz für Sie ein abstraktes – oder noch kein erlebtes musikalisches – Phänomen ist, empfehle ich Ihnen folgendes einfaches Experiment: Suchen sie ein Klavier (kein digitales) und auf dem Klavier einen Ton, den Sie gut singen können. Drücken Sie die Taste mit diesem Ton und singen Sie ihn. Das setzt natürlich schon die Resonanz in ihrem Innenohr voraus, sonst würden Sie den Ton nicht treffen. Als nächstes drücken Sie die Klaviertaste, aber so, dass kein Ton erklingt und halten Sie die stumme Taste nach unten gedrückt. So kann die Saite frei schwingen. Jetzt singen Sie den Ton wieder. Wenn Sie die Tonhöhe der Taste erwischt haben, dann erklingt jetzt der Ton im Klavier, ohne dass Sie die Taste erneut anschlagen. Am besten funktioniert das, wenn das Klavier offen ist, und Sie die Saiten sehen können. Aber auch bei geschlossenem Klavierdeckel funktioniert es, Sie müssen eventuell nur ein bisschen lauter singen. Sie können nun verschiedene Töne singen, z.B. eine kleine Melodie und erkennen, dass der Ton im Klavier genau dann erklingt, wenn Ihre Stimme die gleiche Tonhöhe hat wie die Taste.

Falls Sie Mühe haben, den Ton zu treffen, geht es noch einfacher. Drücken Sie auf dem Klavier das Pedal ganz rechts. Jetzt können alle Saiten frei schwingen. Rufen Sie jetzt laut auf das Klavier ein, am besten bei offenem Deckel. Wieder hören Sie, wie die Saiten schwingen, als Echo auf ihre Stimme.

Einfache Resonanz

Die «Fernwirkung» im obigen Experiment ist keine Hexerei, sondern durch Schallwellen vermittelt. Diese treten mit der Saite in Resonanz. Das typische daran ist, dass die Resonanz nicht bei jeder Frequenz auftritt, sondern genau dann, wenn die Schallwelle die Eigenfrequenz der Saite trifft. Eigenfrequenzen sind Eigenschaften von vielen physikalischen Systemen, z.B. kann auch eine Brücke eine Eigenfrequenz haben oder ein Glas, ein Stück Holz oder ein Topf. Saiten- und Blasinstrumente sind dahingehend perfektioniert, dass sie besonders gut klingen, d.h. dass ihre Eigenfrequenzen besonders kräftig und klangvoll sind.

Resonanzen höheren Grades

Wieder schlage ich ein kleines Experiment vor und wieder benötigen Sie ein Klavier, diesmal sollte es gestimmt sein.

Abb 1: Zwei C’s auf dem Klavier im Abstand einer Oktave

Drücken Sie nun die Taste C auf dem Klavier, und zwar die obere (rechte) Taste C. Auf dem Klavier hat es natürlich viele von diesen C’s, nehmen Sie am besten zwei benachbarte C’s in der Mitte der Tastatur, dort ist das Experiment am deutlichsten zu hören. Sie können auch andere Töne als C’s nehmen, das Experiment funktioniert mit allen Tönen, Voraussetzung ist allerdings, dass der Abstand zwischen den beiden Tönen genau eine Oktave ist. Sie erkennen jetzt auch, woher die Oktave ihren Namen hat, das obere C ist acht (lateinisch: octo) Töne vom unteren entfernt (bei der Zählung wird für die musikalischen Intervalle der Ausgangston immer mitgezählt).

Sie haben jetzt die obere (rechte) C-Taste stumm nach unten gedrückt. Schlagen sie jetzt die untere C-Taste kurz und kräftig an. Sie hören jetzt wieder eine «Fernwirkung». Offensichtlich ist die Saite des oberen C’s durch den Anschlag des unteren in Schwingung geraten. Schlagen Sie nun eine Taste gleich links oder rechts neben dem unteren C an. Bei diesen Tasten können Sie das obere C nicht zum Klingen bringen, es entsteht keine Resonanz.

Weshalb genau bei einer Oktave eine Resonanz entsteht

Grundton und Obertöne

Abb. 2:  Mögliche Schwingungen einer Saite
In Abb. 2 sehen Sie fünf mögliche Schwingungsmuster für eine gespannte Seite. Unten (bei 1) schwingt die Saite mit genau einem Bauch in der Mitte. Bei 2 hat es zwei Bäuche, bei 5 fünf. Gelb ist die schwingende Saite gezeichnet, der schwarze Strich zeigt die korrespondierende Schallwelle, d.h. die Schallwelle (Wanderwelle), welche die gleiche Frequenz hat wie die stehende Welle, welche die klingende Saite darstellt. Diese Frequenz hat die Wellenlänge λ, ist also doppelt so lang wie die Saite.

Der Zustand 1 ist nun der Grundzustand, d.h. der Ton, der im oben vorgeschlagenen Experiment erklingt, wenn Sie eine Klaviertaste drücken. Der Zustand 2 ist der nächste erlaubte Zustand der Schwingung. Hier schwingt die Saite mit zwei Bäuchen, bei 3 sind es drei, etc. Alle Zustände also, bei denen die Saite an den Enden, an denen sie befestigt ist, nicht ausschwingt, sind Zustände, die ein ungehindertes Schwingen der Saite erlauben. Somit ist nicht nur der Zustand der einfachen Saitenschwingung möglich, sondern im Prinzip jeder, der einer Wellenlänge entspricht, die ganzzahlig in die Saitenlänge passt. Bei Zustand 2 ist die Wellenlänge halb so lang wie im Grundzustand und die Frequenz somit doppelt so gross (schnell,hoch). Zustand 2 entspricht mit seiner doppelt so grossen Frequenz dem Ton, der eine Oktave höher klingt, Zustand 4 dem Ton, der zwei Oktaven höher klingt.

Weshalb nun klingt das höhere C nun mit, wenn Sie, wie im Experiment oben vorgeschlagen, das tiefere C anschlagen? – Der Grund liegt darin, dass die Saite des tiefen C’s – wie jede Saite – nicht nur in der Grundschwingung (Zustand 1 in Abb. 2) erklingt, sondern mehr oder weniger in allen erlaubten Schwingungen. Diese Schwingungen überlagern sich also. Wenn nun die von der tieferen Saite ausgehenden Schallwellen die Saite des höheren C’s erreichen, dann enthalten sie neben der Grundschwingung immer etwas leiser auch die höheren Schwingungen und somit genau auch die Schwingung der Saite des höheren C’s. Einer Resonanz steht dadurch nichts mehr im Weg.

Sinusschwingung und Obertöne

Die schwarzen Kurve in Abb. 2 sind mathematisch gesehen Sinuskurven. Mit einem technischen Gerät ist es möglich, solche Kurven akustisch zu erzeugen, man spricht dann von einem Sinusschwingung. Mit natürlichen Klangkörpern, also der Klaviersaite, Ihrer Stimme oder überall sonst in der Natur kommen solche reinen Sinusschwingungen nicht vor, sondern die so erzeugten Schallwellen enthalten immer auch die höheren Schwingungen (Stufen 2 ff. in Abb. 2) in komplexen Überlagerungen mit. Man spricht von Obertönen. Die Anteile der einzelnen Obertöne, d.h. wie viel von den Schwingungen der Stufen 2 und folgende jeweils neben dem Grundton in der Mischung des Klangs mitschwingt, ist sehr variabel und wird von den physikalischen Eigenschaften des klangerzeugenden Mediums bestimmt. Diese Mischungen machen den Charakter des Klangs des jeweiligen Instruments aus.

Interpretation der Saitenschwingungen in den drei Welten

Platonisch → Physikalisch (Von einfach zu komplex)

Wir sehen am Beispiel der schwingenden Saite, wie mathematische Gesetzmässigkeiten aus der  platonischen Welt die physikalische Welt bestimmen. In der physikalischen Welt kommen sie aber sehr verschieden an und es entsteht eine grosse Vielfalt: Auf der Saite entstehen gleichzeitig mehrere Schwingungen, neben dem Grundton entstehen immer gleichzeitig viele Obertöne. Jede einzelne dieser Schwingungen kann mathematisch sehr einfach beschrieben werden. Die Mischung jedoch ist äusserst komplex.

Was mathematisch, d.h. in der abstrakten platonischen Welt sehr einfach ist, wird schnell komplex, sobald es in der physikalischen Welt wirkt.

Die unendliche Treppe in Penrose und «Anti-Penrose»-Richtung

Die Trichter in der Skizze von Penrose stellen m.E. nur eine Richtung der Verhältnisse dar. Penrose betont in seiner Darstellung, dass nicht die ganze Mathematik gebraucht wird, um die Physik zu beschreiben und kommt so zu Mengenverhältnissen, wie sie in der Skizze mit den Trichtern dargestellt sind und die wie die ewige Treppe der Logik zu widersprechen scheinen.

Doch meines Erachtens können die Trichter auch in der Gegenrichtung gesehen werden, dann wenn man die Informationsmenge betrachtet. Diese ist in der physikalischen Welt grösser als in der platonischen. Beim Eintreten der Mathematik in die Physik entsteht Neues, nämlich die komplexe Vielfalt der Mischungsverhältnisse. Diese konkrete Vielfalt in der physikalischen Welt stellt eine Information dar, die weit über die Information der ursprünglichen mathematischen Welt hinausgeht. Die Informationsmenge nimmt in Richtung von platonisch zu physikalisch zu. Das stellt mengenmässig eine Gegenbewegung zum Trichter von Penrose dar. Die unendliche Treppe der drei Welten verliert so bei näherem Hinsehen etwas von ihrem Paradoxie-Schrecken.

Platonisch → Mental

Vermutlich haben Sie schon technisch erzeugte Sinusschwingungen gehört. Sie standen am Anfang der elektronischen Musik und hatten damals den Reiz des Neuen und Technischen. Gerade ihre nackte Reinheit war beeindruckend. Allerdings sind diese Töne sind sehr schnell auch sehr langweilig. Die Reinheit und die sterile Banalität dieser technischen Klänge ist verursacht durch das fehlende Mitschwingen der Obertöne. Die reichhaltigen Informationen dieser Zusatzschwingungen nehmen wir als Hörer wahr und sie machen den Reichtum der natürlichen Klänge aus. Ich möchte nicht auf sie verzichten.

In einem Fortsetzungsbeitrag möchte ich erklären, weshalb die Oktave in der mentalen Welt so wichtig ist und was das dazu beiträgt, dass die Tonleitern in allen Kulturen stets die Oktave als Basis haben.

Dies ist ein Beitrag zur Entstehung der Tonleitern

 

Drei-Welten-Theorie, Information

Die Oktave

Hinterlassen Sie einen Kommentar

Eine bemerkenswerte Gemeinsamkeit

Alle Tonleitern, die ich kenne, bewegen sich im Bereich einer Oktave. Auch Tonleitern, die für uns Europäer ungewöhnlich klingen, arabische, indische, japanische und afrikanische bewegen sich innerhalb genau einer Oktave, d.h. ihr tiefster und ihr höchster Ton haben den Abstand von genau einer Oktave, was für eine Tonart das auch ist.

Ich finde das äusserst bemerkenswert. Das ist so, als ob alle Sprachen der Welt, die ja sehr unterschiedliche Wörter haben, für einen bestimmten Begriff das gleiche Wort verwenden würden, und zwar schon immer und ganz unabhängig voneinander. Woher kommt das?

Die Drei-Welten-Theorie kann nun diese ungewöhnliche Gemeinsamkeit der Tonarten aller menschlichen Kulturen plausibel erklären.

Die Oktave platonisch

Wenn Sie eine Saite auf einer Geige zupfen, erhalten Sie einen Ton. Wenn Sie nun den Finger genau in der Mitte der Saite auf das Griffbrett drücken und dann zupfen, erklingt die Saite eine Oktave höher. Das gleiche gilt für Pfeifen. Eine Pfeife, die halb so lang ist wie eine andere, klingt eine Oktave höher. Offensichtlich liegt der Oktave ein Verhältnis 1:2 zugrunde. Das ist die platonische, d.h. mathematische Seite der Oktave. Einfache mathematischen Verhältnisse (= Brüche) spielen auch bei anderen Intervallen eine Rolle, worauf wir noch kommen werden.

Diese mathematischen Verhältnisse der Verhältnisse zwischen den Tönen – das heisst der Intervalle – sind schon lange bekannt und wurden vom Griechen Pythagoras gelehrt, der vor Sokrates und Platon eine einflussreiche Schule in Süditalien begründete.

Abb. 1: Eine schwingende Saite. Oben ist die Saite links und rechts (0 und 1) befestigt, kann dort also nicht schwingen. Je weiter weg von der Befestigung, umso stärker schwingt sie aus, am meisten in der Mitte. Unten ist in der Mitte ein Finger auf die Seite gedrückt, und sie schwingt nun in der halben Länge und eine Oktave höher. (Mit diesen Beschreibungen sind wir aber von der platonischen bereits in die physikalischen Welt eingetreten).

Das einfaches Zahlenverhältnis erklärt die Einzigartigkeit des gemeinsamen Merkmals Oktave über alle menschlichen Kulturen noch nicht. Weshalb spielt das Zahlenverhältnis für die Tonleitern überhaupt eine Rolle?

Zur Erklärung müssen wir die beiden anderen Welten ansehen, nämlich die physikalische, in der Töne erklingen, und die mentale, in der wir sie wahrnehmen.

Die Oktave physikalisch

Töne

Töne sind materielle Schwingungen in einem Trägermedium, z.B. Luft. Ein Ton enthält ist in der Regel eine Überlagerung von mehreren Schwingungen (Grundton plus Obertöne). An dieser Stelle schauen wir aber nur die Grundschwingung an, die die erkennbare Tonhöhe bestimmt.

Diese Grundschwingung ist eine Sinuskurve und die Tonhöhe wird als Frequenz angegeben, z.B. 440 Hz. Diese Frequenz bedeutet, dass die Sinuskurve 440 mal pro Sekunde hin und her schwingt. Das gleiche tut auch die Saite.

Die Saite schwingt an Ort, man spricht von einer stehenden Welle (siehe Abb. 1 oben). Die Schwingung in der Luft hingegen bewegt sich vom Ort fort (Wanderwelle). Durch ihre stationären Schwingung kann die Saite die Luft bewegen und führt so zu einer Schwingung in der Luft, einer Schallwelle. Dabei überträgt die Saite die Eigenschaften ihrer Schwingung, insbesondere deren Frequenz, auf die Schallwelle.

Die Wellenlänge in einer Wanderwelle, also einer Schallwelle, aber auch z.B. einer Welle auf der Wasseroberfläche ist der Abstand der Wellenbäuche (oder Wellenkämme)  voneinander. Bei einer stehenden Welle, also der Saite in Abb. 1 ist die Wellenlänge gleich der (doppelten) Länge der schwingenden Saite.

Wenn nun die Geschwindigkeit der Wanderwelle konstant ist, dann müssen mehr Wellenbäuche hintereinander kommen, je kürzer die Abstände zwischen ihnen sind. Die Abstände zwischen den Wellenkämmen entsprechen der Wellenlänge, die Zahl der Kämme pro Zeit der Frequenz der Welle. Je mehr Kämme an einem Ort durchlaufen, umso kleiner sind ihre Abstände.

Zwischen der Wellenlänge und ihrer Frequenz besteht somit ein umgekehrt proportionales Verhältnis, d.h. je kürzer die Wellenlänge umso höher muss die Frequenz sein. Deshalb schwingt die halb so lange Saite doppelt so schnell. Das ist der physikalische Ursprung der Oktave.

Tonentstehung

Wie kommt nun die Schwingung in die Saite? Dies rührt daher, dass eine gespannte Saite eine Tendenz zu einer Eigenschwingung hat, Die Spannung der Saite führt dazu, dass ein Anstoss, z.B. ein Zupfen der Saite, in ihr eine Bewegung auslöst, die an den beiden Enden der Saite nicht aufhört, sondern wieder zurück gestossen wird. Auf diese Weise bildet sich die stehende Welle aus. Die Wellenlänge, also der Abstand der Wellenbäuche, wird dabei von der Länge der Saite bestimmt. Der Grund dafür ist, dass an den beiden Enden der Saite keine Bewegung mehr möglich ist, da sie ja dort fest fixiert ist. Ausschwingen kann die Welle nur dazuwischen. Die Wellenlänge muss also genau in die Länge der Saite passen.

Die Oktave mental

Das Innenohr

Wir nehmen Töne mit unseren beiden Innenohren wahr. Diese sind äusserst raffiniert gebaute Organe mit einer schneckenförmigen Struktur, weshalb man auch von der Hörschnecke spricht. Die Schallwelle durchwandert von aussen her die flüssigkeitsgefüllte Hörschnecke und erzeugt durch Resonanz eine Schwingung der sogenannten Basilarmembran, welche  die gesamte Schnecke durchzieht. Entlang der Basilarmembran nehmen sogenannte Haarzellen die Schwingungen der Basilarmembran auf und leiten sie als elektrische Signale nach innen ins Hirn. Durch den komplexen und raffinierten Bau der Schnecke, der hier nur kursorisch beschrieben ist, können die akustischen Signale analytisch zerlegt werden, sodass je nach Frequenz unterschiedliche Haarzellen angeregt werden, je höher die Frequenz umso näher am Eingang der Schnecke, je tiefer umso mehr im Innern.

Die Tonwahrnehmung mental

Bis hier hat die Beschreibung der Tonwahrnehmung über das Innenohr noch nichts mit der mentalen Welt zu tun, es handelt sich nur um die anatomischen Voraussetzungen, d.h. den physikalischen Apparat, der die physikalischen Signale (die Schallwellen) gezielt für die eigentliche Wahrnehmung vorbereitet. Diese findet im Gehirn statt und ist ein subjektiver Vorgang.

Subjektive Vorgänge zeichnen sich dadurch aus, dass sie nicht von aussen nachvollzogen werden können. Wie Sie etwas hören und empfinden, weiss ich nicht, das ist ganz Ihre Welt. Allerdings haben wir als Menschen so viele Gemeinsamkeiten, dass ich in davon ausgehen kann, dass Sie vieles ganz ähnlich erleben wie ich. Wir haben die gleiche Anatomie und die gleichen Lebensbedingungen. Weshalb empfinden viele Menschen die gleiche Musik als schön? Wenn wir von der gleichen Musik gerührt werden, sie gleich wie andere als fröhlich, traurig, tröstend, mitreissend usw. empfinden, zeigt das, dass unsere mentalen Welten trotz ihrer Subjektivität stark verbunden sind.

Dabei spielen kulturelle Aspekte – also gelernte Gewohnheiten – eine ganz wichtige Rolle. Auch die Kultur gehört letztlich in die mentale Welt, sie ist der Geist, d.h. die Subjektivität, die wir teilen. Diese Subjektivität, die individuelle wie die kollektive, fusst aber auch auf den physikalischen Voraussetzungen.

Somit sind wir wieder bei unserem Thema: Weshalb haben alle Kulturen der Menschen die Oktave in ihren sonst so verschiedenen Tonleitern?

Der Grund ist physikalisch erklärbar und liegt in der Resonanz.

Die Resonanz

Resonanz ist eine Voraussetzung, dass die Töne im Innenohr überhaupt ankommen. Denn die Basilarmembran im Innenohr übernimmt die Schwingungen der Schallwellen auf eine ganz bestimmte Weise. Nicht alle Frequenzen finden auf der Basilarmembran die gleiche Resonanz. Das Innenohr ist so gebaut, dass die Basilarmembran am Eingang mit hohen Frequenzen in Resonanz gerät und in der Tiefe mit tiefen. So analysiert das Ohr die verschiedenen Tonhöhen. Aber die Resonanz ist noch für viel mehr verantwortlich, u.a. auch dafür, dass in den tausenden unterschiedlichen Tonleitern die Oktave immer vorkommt. Dieser auffällige Beobachtung werden wir im Fortsetzungsbeitag verfolgen.

Dies ist ein Beitrag zur Entstehung der Tonleitern

 

Drei-Welten-Theorie

Die physikalische Welt

Hinterlassen Sie einen Kommentar

Die Welt der Naturwissenschaften

Die physikalische Welt ist das, was die Naturwissenschaften untersuchen, allen voran die Physik. Die Erfolge des naturwissenschaftlichen Programms sind offensichtlich, sowohl bezüglich der Einblicke in das Funktionieren der Welt, also der Theorie, wie auch bezüglich der dadurch ermöglichten Techniken, also der Praxis. Die Naturwissenschaften haben unsere Welt seit Galileo Galilei fundamental verändert.

Objektivität

Der Erfolg wurde dadurch möglich, dass sich die Denker und Forscher in Europa seit der Renaissance nicht mehr auf das beriefen, was von altersher überliefert war, sondern vorurteilsfrei selber forschten und suchten. Während die Mönche in den Klöstern alte Schriften interpretieren und kompilierten (Scholastik), wagten die freien Geister das zu glauben, was sie in der Natur selber sehen konnten – auch wenn es im Widerspruch zu klösterlichen Autoritäten war.

Mit dem Wegfall der alten Autoritäten brauchte es aber eine neue Richtschnur, damit nicht jeder irgendetwas behaupten konnte. Die These eines Forscher sollte unabhängig überprüfbar sein, und nur das sollte fortan als wahr und zutreffend gelten, was von allen zweifelsfrei beobachtbar ist. Das Ideal der Objektivität war geboren.

Messbarkeit

Aber nicht nur objektiv, d.h. von jedermann überprüfbar, sondern auch ganz genau sollte die Welt beschrieben werden können. Das hat zwei Vorteile: a) Eine These ist umso glaubhafter, je präziser ihre Voraussagen sind. Je genauer gemessen werden kann, umso aussagekräftiger werden die Beobachtungen. b) Neben präziseren Erkenntnissen erlauben die genauen Messungen auch den Bau von immer präziseren Apparaten.

Die Welt von aussen

Die Naturwissenschaften konzentrierten sich somit darauf, was von aussen gesehen und gemessen werden kann. Das ist das, was Penrose als die physikalische Welt bezeichnet. Nicht meine Innensicht, meine Empfindung oder mein Glaube ist gefragt, sondern das, was sich zweifelsfrei von aussen beobachten und messen lässt. Das ist die physikalische Welt.

Die physikalische Welt im Zusammenspiel

Man könnte nun die physikalische Welt als die einzig wahre Wirklichkeit ansehen, doch wird unser Weltbild plastischer, wenn wir die beiden anderen Welten hinzunehmen. Wie spielen die drei Welten zusammen? – Es gibt Brücken von einer zur anderen, es gibt Übergänge, und es gibt Wirkungen von einer Welt in die anderen. Wie das funktioniert, lässt sich am Beispiel der Musik ausführen, die an allen drei Welten teilhat.

Dies ist ein Beitrag zur Drei-Welten-Theorie.

Drei-Welten-Theorie, Logik

Die Drei-Welten-Theorie (Roger Penrose)

Hinterlassen Sie einen Kommentar

Die drei Welten

Es gibt praktische Fragen, die mit unseren konkreten Leben zu tun haben, und theoretische Fragen, die damit scheinbar nichts zu tun haben. Es gibt aber auch theoretische Überlegungen, die durchaus mit unserem praktischen Alltag zu tun haben. Eine davon ist die Drei-Welten-Theorie, die sich damit beschäftigt, in welchen Welten wir konkret leben.

Auf welchem Grund steht unsere ganz alltägliche Existenz? Die Drei-Welten-Theorie weist darauf hin, dass wir uns gleichzeitig in drei grundverschiedenen Welten bewegen. Praktisch stellt das für uns kein Problem dar, theoretisch hingegen stellt sich die Frage, wie drei so verschiedene Welten sich denn in der Realität überhaupt begegnen können.

Bei Roger Penrose heissen die drei Welten:
A) Platonic World
B) Physical World
C) Mental World

Hier ist die originale Darstellung von Roger Penrose:

Platonic World: Die Welt der Ideen. Mathematik z.B. befindet sich gänzlich in der platonischen Welt.

Physical World: Die reale, physische Welt mit Dingen, die zu einem bestimmten Zeitpunkt an einen bestimmten Ort sind.

Mental World: Meine subjektiven Wahrnehmungen, die mich die anderen Welten erst erkennen lassen. Aber auch meine Gedanken und Vorstellungen, so wie ich sie erlebe.

Das Kreisverhältnis zwischen den drei Welten

Die Pfeile zwischen den Kugeln deuten das Kreisverhältnis an, das diese Welten nach Penrose miteinander eingehen:

Platonic → Physical: Hinter der Physik steckt Mathematik. Physik ist ohne höhere Mathematik undenkbar. Offensichtlich hält sich die physikalische Welt sehr genau an mathematische Gesetze. Wird die Realwelt also von der Mathematik bestimmt?

Physical → Mental: Mein Hirn ist ein Gegenstand der physikalischen Welt. Nach gängiger Vorstellung bestimmen die Neuronen des Hirngewebes mit ihren elektrischen Schaltungen meine Hirnleistungen.

Mental → Platonic: Grosse Denker sind in der Lage, in Gedanken (Mental World) die Gesetze der Mathematik zu formulieren, sie ‹entstehen› in ihrem Kopf.

Das ist also der Kreisprozess:
Die platonische Welt (Mathematik) bestimmt die physikalische. Diese ist die Basis für das menschliche Denken. Im menschliche Denken wiederum haben Mathematik (und andere Ideen) ihren Platz. Die mathematischen Gesetze … hier schliesst sich der Kreis.

Mächtigkeiten der drei Welten

Interessant sind auch die sich öffnenden Trichter in Penrose’s Skizze, die zusammen mit den Pfeilen von einer Welt zur nächsten weisen. Penrose deutet damit an, dass die im Kreisprozess folgende Welt nur einen Teil der Welt benötigt, aus der sie während des Generierungsprozesses entsteht.

Platonic → Physical: Nur ein kleiner Teil der mathematischen Erkenntnisse kann in der Physik verwendet werden. So gesehen brauchen (sind?) die physikalischen Gesetze nur einen Ausschnitt aus der Mathematik.

Physical → Mental: Mein Hirn ist ein sehr kleiner Teil der physikalischen Welt.

Mental → Platonic: Mein Hirn beschäftigt sich mit vielem; Mathematik und abstrakte Ideen sind nur ein Teil davon.

Die Platonische Welt ist dann wieder Ursprung für die physische Welt. Die Grössenverhältnisse scheinen dabei aber nicht richtig aufzugehen. Das gleicht der berühmten ewigen Treppe:

Die ewige Treppe

Nebenbemerkung:
Die ewige Treppe wurde  von Roger Penrose’s Vater, Lionel Penrose enteckt und wird auch Penrose-Treppe genannt  – bzw. Escher-Penrose-Treppe nach dem holländischen Grafiker, der u.a. Douglas Hofstadter zu seinem Buch ‹Gödel, Escher, Bach› inspiriert hat. Die Endlosigkeit, mit der die Treppe steigt, ist grafisch scheinbar mühelos darstellbar, logisch jedoch höchst verzwickt (selbstreferenzielles Tabu).

Für Penrose liegt ein Geheimnis in den drei Welten. Er schreibt:

«Zweifellos gibt es in Wirklichkeit nicht drei Welten, sondern nur eine, und das wahre Wesen dieser Welt können wir gegenwärtig nicht einmal erahnen.»

Es geht also um drei Welten in einer – und somit um ihre Unterschiede und die Art ihrer Verschränkung.

Keine abstrakte Theorie

Die drei Welten sind keine abstrakte Theorie, sondern lassen sich in unserer eigenen privaten Erlebniswelt erkennen. Sie spielen z.B. in der Musik eine wichtige Rolle. Am Beispiel der Musik kann man auch erkennen, wie die drei Welten zusammenwirken. Mehr dazu später auf dieser Website (siehe Übersichtseite zur Drei-Welten-Theorie).

Nachtrag im Oktober 2020:

Ich habe diesen Beitrag einen Monat vor der Bekanntgabe, dass Sir Roger Penrose den Nobelpreis bekommt, geschrieben. Ich freue mich sehr, dass dieser geniale Wissenschaftler den Preis bekommt.

Dies ist der Startbeitrag zum Thema Musikalische Tonleitern und Drei-Welten-Theorie.