Regelbasiert im Vergleich zu korpusbasiert
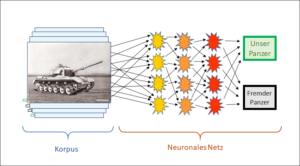
Die korpusbasierte KI (Typus «Panzer», siehe KI-Einstiegsbeitrag) konnte ihre Schwächen erfolgreich überwinden (siehe Vorbeitrag). Dafür reichte eine Kombination von «Brute Force» (verbesserte Hardware) und einem idealen Opportunitätsfenster, als nämlich während der superheissen Expansionsphase des Internets Firmen wie Google, Amazon, Facebook und viele andere grosse Datenmengen sammeln und damit ihre Datenkorpora füttern konnten. Und mit einem ausreichend grossen Datenkorpus steht und fällt die korpusbasierte KI.
für die regelbasierte KI aber reichte «Brute Force» nicht aus. Es nützte auch nichts, viele Daten zu sammeln, da für den Regelbau die Daten auch organisiert werden müssen – und zwar grossenteils von Hand, also durch menschliche Fachexperten.
Herausforderung 1: Unterschiedliche Mentalitäten
Nicht alle Menschen sind gleichermassen davon fasziniert, Algorithmen zu bauen. Es braucht dazu eine besondere Art Abstraktionsfähigkeit, gepaart mit einer sehr gewissenhaften Ader – jedenfalls was die Abstraktionen betrifft. Jeder noch so kleine Fehler im Regelbau wird sich unweigerlich auswirken. Mathematiker verfügen sehr ausgeprägt über diese hier gefragte konsequent-gewissenhafte Mentalität, aber auch Naturwissenschaftler und Ingenieure zeichnen sich vorteilhaft dadurch aus. Natürlich müssen auch Buchhalter gewissenhaft sein, für den Regelbau der KI ist aber zusätzlich noch Kreativität gefragt.
Verkäufer, Künstler und Ärzte hingegen arbeiten in anderen Bereichen. Oft ist Abstraktion eher nebensächlich, und das Konkrete ist wichtig. Auch das Einfühlungsvermögen in andere Menschen kann sehr wichtig sein. Oder man muss schnell und präzis handeln können, z.B. als Chirurg. Diese Eigenschaften sind alle sehr wertvoll, für den Algorithmenbau aber weniger wichtig.
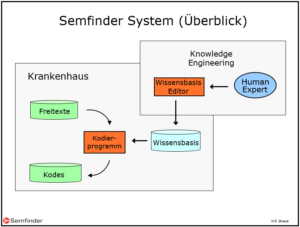
Das ist für die regelbasierte KI ein Problem. Denn für den Regelbau braucht es sowohl die Fähigkeiten des einen und als auch das Wissen des anderen Lagers: Es braucht die Mentalität, die einen guten Algorithmiker ausmacht, gepaart mit der Denkweise und dem Wissen des Fachgebiets, auf das sich die Regeln beziehen. Eine solche Kombination des Fachgebietswissens mit dem Talent zur Abstraktion ist selten zu finden. In den Krankenhäusern, in denen ich gearbeitet habe, waren die beiden Kulturen in ihrer Getrenntheit ganz klar ersichtlich. Hier die Ärzte, die Computer höchstens für die Rechnungsstellung oder für gewisse teure technische Apparate akzeptierten, die Informatik allgemein aber gering schätzten, und dort die Informatiker, die keine Ahnung davon hatten, was die Ärzte taten und wovon sie überhaupt sprachen. Die beiden Lager gingen sich meist einfach aus dem Weg. Selbstverständlich war es da nihct verwunderlich, dass die für die Medizin gebauten Expertensysteme meist nur für ganz kleine Teilgebiete funktionierten, wenn sie nicht im blossen Experimentierstadium verharrten.
Herausforderung 2: Wo finde ich die Experten?
Experten, die kreativ und in den beiden Mentalitätslagern gleichermassen zuhause sind, sind selbstverständlich schwer zu finden. Erschwerend kommt hinzu: Es gibt kaum Ausbildungsstätten für diese Art Experten. Realistisch sind auch folgende Fragen: Wo sind die Ausbildner, die sich mit den aktuellen Herausforderungen auskennen? Welche Diplome gelten wofür? Und wie evaluiert ein Geldgeber auf diesem neuen Gebiet, ob die eingesetzten Experten taugen und die Projektrichtung stimmt?
Herausforderung 3: Schiere Menge an nötigen Detailregeln
Dass eine grosse Menge an Detailwissen nötig ist, um in einer Realsituation sinnvolle Schlüsse zu ziehen, war schon für die korpusbasierte KI eine Herausforderung. Denn erst mit wirklich grossen Korpora, d.h. dank des Internets und gesteigerter Computerleistung gelang es ihr, die riesige Menge an Detailwissen zu erfassen, das für jedes realistische Expertensystem eine der Basisvoraussetzungen ist.
Für die regelbasierte KI ist es aber besonders schwierig, die grosse Wissensmenge bereitzustellen, denn sie braucht für die Wissenserstellung Menschen, welche die grosse Wissensmenge von Hand in computergängige Regeln fassen. Das ist eine sehr zeitraubende Arbeit, die zudem die schwierig zu findenden menschlichen Fachexperten erfordert, die den oben genannten Herausforderungen 1 und 2 genügen.
In dieser Situation stellt sich die Frage, wie grössere und funktionierende Regelsysteme überhaupt gebaut werden können? Gibt es eventuell Möglichkeiten, den Bau der Regelsysteme zu vereinfachen?
Herausforderung 4: Komplexität
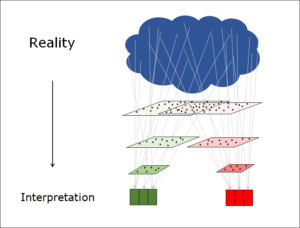
Wer je versucht hat, ein Fachgebiet wirklich mit Regeln zu unterfüttern, merkt, dass er schnell an komplexe Fragen stösst, für die er in der Literatur keine Lösungen findet. In meinem Gebiet des Natural Language Processing (NLP) ist das offensichtlich. Die Komplexität ist hier nicht zu übersehen. Deshalb muss unbedingt auf sie eingegangen werden. Mit anderen Worten: Das Prinzip Hoffnung reicht nicht, sondern die Komplexität muss thematisiert und intensiv studiert werden.
Was Komplexität bedeutet, und wie man ihr begegnen kann, darauf möchte ich in einem weiteren Beitrag eingehen. Selbstverständlich darf dabei die Komplexität nicht zu einer übermässigen Regelvermehrung führen (siehe Herausforderung 3). Die Frage, die sich für die regelbasierte KI stellt, ist deshalb: Wie kann ein Regelsystem gebaut werden, das Detailhaltigkeit und Komplexität berücksichtigt, dabei aber einfach und übersichtlich bleibt?
Die gute Botschaft ist: Auf diese Frage gibt es durchaus Antworten.
Dies ist ein Beitrag zum Thema künstliche Intelligenz (KI). In einem Folgebeitrag werden die Herausforderungen präzisiert.