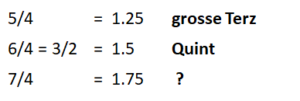Auf dieser Seite erkläre ich einige Regeln, die gelten, wenn wir mit Intervallen und ihren Frequenzen rechnen.

Intervalle sind Brüche

Ein Intervall geht von einem tieferen zu einem höheren Ton. Der Bruch des Intervalls rechnet sich, indem die Frequenz des höheren durch die Frequenz des tieferen Tons geteilt wird, z.B.

E  =  330 Hz
A  =  440 Hz

440/330 = 4/3. Das ist eine Quart. Das Intervall der Quart ist immer 4/3, der höhere Ton ist in der Quart genau 4/3 mal so schnell wie der tiefere.

Dabei kommt es nur auf die relativen Werte an, nicht auf die absoluten. Ob ich die Quart beim E beginne (E-A) oder beim C (C-F) ist egal, das relative Frequenzverhältnis ist immer 4/3. Mit anderen Worten, Intervalle sind immer relativ.

Der exponentielle Verlauf der Frequenzen

Wenn wir Intervalle miteinander vergleichen, gibt es eine entscheidende Besonderheit: Der Frequenzverlauf ist exponentiell.

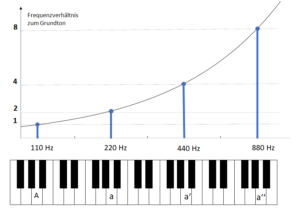
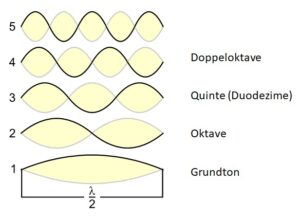
Abb 1: Der Frequenzverlauf ist exponentiell

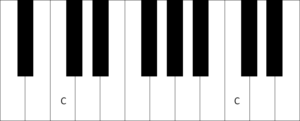
In Abb. 1 sehen Sie die Frequenzen von verschiedenen A Tönen, vom grossen A bis zum zweigestrichenen a". Auf der Klaviertastatur sieht es so aus, als wären die Abstände zwischen allen vier A’s die gleichen, doch wenn wir die Frequenzen anschauen, ist werden die Abstände immer grösser. Mit anderen Worten: Die Frequenzen steigen schneller an als die Intervalle. Mathematisch gesehen verlaufen die Intervalle linear, während die Frequenzen exponentiell verlaufen. Das hat nun einige Konsequenzen für das Rechnen mit den Intervallen.

Intervalle addieren

Wenn wir zwei Intervalle addieren, dann ist das bezüglich der Frequenzen eine Multiplikation. So hat der Ton (gross) A die Frequenz 110 Hz. Wenn wir eine Oktave höher gehen, so hat das (kleine) a eine Oktave höher die doppelte Frequenz, nämlich 220 Hz. Der Abstand zwischen 110 Hz und 220 Hz ist 110 Hz. Doch diese 110 Hz sind nur dann eine Oktave, wenn wir vom grossen A ausgehen. Wenn wir vom kleinen a jetzt wieder eine Oktave hochgehen, dürfen wir nicht die 110 Hz der tieferen Oktave dazuzählen (was 330 Hz gäbe), sondern wir müssen 220 Hz dazugeben und gelangen so von 220 Hz auf 440 Hz.

Unsere spontane Vorstellung, dass eine Oktave einem Wert in Hz entspricht, ist nicht zutreffend. Die Oktave bedeutet, dass die tiefere Frequenz mit 2 multipliziert wird (mit 2 weil die Oktave immer verdoppelt). Aus der Addition der Intervalle wird also eine Multiplikation. Dieser Wechsel der Rechenoperation ist auf den ersten Blick verwirrlich, doch wenn man es weiss, ist die Sache nicht so schwierig. Wir prägen uns deshalb ein:

Addition (von Intervallen) wird zur Multiplikation (von Frequenzen)

Intervalle subtrahieren 

Nicht überraschen ist es bei der Subtraktion ganz analog. Aus der Subtraktion wird eine Division.

Beispiel

Wir suchen den Abstand zwischen einer grossen Terz und der darüberliegenden Quinte. Unser Musikwissen sagt uns, dass der Abstand zwischen den beiden Intervallen eine kleine Terz ist. Können wir das auch ausrechnen?

Bei diesem Vergleich ziehen wir von der Quint die grosse Terz ab. Aber statt abzuziehen, dividieren wir:

Quinte            = 3/2
Grosse Terz = 5/4

Quinte – grosse Terz →3/2 : 5/4 = 3×4 / 2×5 = 12/10 = 6/5

6/5 ist bekanntlich die kleine Terz. Diese Methode funktioniert immer, für alle Intervalle:

Wir können zur Kontrolle die beiden Terzen wieder addieren und erhalten – selbstverständlich durch eine Multiplikation:

5/4 x 6/5 = 30 / 20 = 3/2

Die grosse und die kleine Terz ergeben auf diese Weise wieder die Quinte (3/2).

Der Vorteil: Wir können kürzen!

Die Verschiebung von Addition und Subtraktion zu Multiplikation und Division hat in Brüchen den Vorteil, dass man wie in den oben stehenden Beispielen oft kürzen kann.

Das hat direkten Einfluss auf die Resonanzen: Immer dann, wenn man kürzen kann, werden die Zahlen in den Brüchen kleiner – und kleine Zähler und Nenner in den Brüchen sind ein Vorteil für eine Resonanz. Dies erklärt auch, weshalb wir in den Intervallen lieber keine höheren Primzahlen als 5 haben. Nicht-Primzahlen wie 6, 8, 9, 10 ff. hingegen lassen sich kürzen, weshalb wir durchaus eine grosse Sekunde (9/8) in den Tonleitern finden, hingegen kein Intervall mit dem Bruch 7/4 oder 8/7.

Tonleitertöne aufeinander beziehen

Wenn wir zwei Töne innerhalb einer Tonleiter vergleichen, um zu entscheiden, ob zwischen ihnen eine Resonanz besteht, beziehen wir sie stets auf den gemeinsamen Grundton. Das hat ganz wesentlich mit dem Charakter von Tonleitern (und Akkorden) zu tun. Auf diesem Grundton (der Tonalität) baut die ganze Tonleiter, bzw. der Akkord auf.

Da die Intervalle stets relativ sind, kommt es nicht auf die absolute Höhe des Tons, d.h. nicht auf die absoluten Frequenzen darauf an. Wir setzen deshalb den

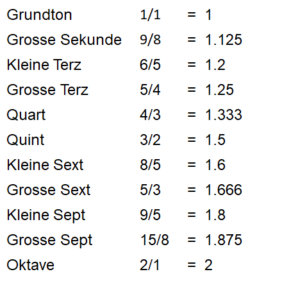
Grundton = 1

Alle anderen Töne geben wir als Intervalle zum Grundton an.

Abstand zwischen zwei Tonleitertönen

Wie verhalten sich z.B. die Quart und die Quint? Die Quart ist 4/3 über dem Grundton, die Quint 3/2. Wenn wir diese beiden Töne vergleichen wollen, können wir den Abstand zwischen ihnen berechnen. Der Abstand ist eine Subtraktion und eine Subtraktion ist bei Frequenzen eine Division. Wir rechne den höheren durch den tieferen Ton und erhalten: 3/2 : 4/3 = 9/8.

9/8 ist eine grosse Sekunde, der Abstand zwischen der Quart und der Quinte ist eine grosse Sekunde.

Resonanz zwischen dem Grundton und zwei Tonleitertönen

Wenn wir zwei Tonleitertöne anschauen, dann haben diese stets den Grundton «im Hinterkopf», bzw. im Fundament. Der Grundton bestimmt die Tonalität, und die Tonalität setzt die relative Tonleiter auf eine absolute Basis.

Wie aber mischen sich die drei Töne – Grundton, Quart und Quinte?

Damit Resonanz entsteht, müssen alle drei Töne auf einer gemeinsame Basis stehen, oder mathematisch ausgedrückt, es braucht so etwas wie eine gemeinsame Zählzeit für alle drei Frequenzen – also für den Grundton (1), die Quart (4/3) und die Quint (3/2).

Dazu suchen wir den kleinsten Nenner, der für alle drei Zahlen aufgeht. Im Beispiel ist es der Nenner 6:

Grundton 1 = 6/6
Quarte  4/3 = 8/6
Quinte  3/2 = 9/6

Dieser gemeinsame Nenner ist immer das kgV, das kleinste gemeinsame Vielfache aller beteiligten individuellen Nenner.

Ein weiteres Beispiel:

Grundton          1 = 15/15
kleine Terz   6/5 = 18/15
grosse Sext  5/3 = 25/15

Das kgV von 1, 5 und 3 ist 15.

Was bedeutet nun dieser gemeinsame Nenner von mehreren Tönen?

Ich stelle die Hypothese auf, dass eine Resonanz sich umso leichter einstellt, je kleiner dieser gemeinsame Nenner ist. Für unsere Resonanzüberlegung gilt auf Basis dieser Hypothese folgendes:

Töne, die einen tiefen gemeinsamen Nenner haben, mischen sich leicht.

Je höher der gemeinsame Nenner ist, umso kleiner ist die interne Resonanz der Töne. 

Über die Konsequenzen dieser Schlüsse berichte ich in den Texten über konkrete Tonleitern und Akkorde.

---

Hier finden Sie die Übersicht über die Texte zur Drei-Welten-Theorie.

Worum geht es?

Nach der 3-Welten-Theorie spielt die Mathematik (ideale Welt) bei physikalischen Prozessen (physikalische Welt) eine Rolle. Ohne unser subjektives Empfinden (mentale Welt) würden wir aber von all dem nichts mitbekommen. Wie diese drei sehr unterschiedlichen Welten in der Realität zusammenkommen, untersuche ich am Beispiel der Tonleitern. Hier gibt es einige Rätsel, z.B. weshalb die menschlichen Kulturen tausende von verschiedenen Tonleitern hervorgebracht haben, aber jede davon die Oktave verwendet.

Diese Konstanz der Oktave kann einfach durch Resonanz erklärt werden, die im Fall der Oktave besonders auffällig ist, weil sie einem mathematischen Verhältnis 2:1 entspricht. Der höhere Ton der Oktave schwingt mit doppelter Frequenz im Vergleich zum Grundton. Ein augenfälliges Beispiel dafür, wie Physik, Mathematik und subjektives Empfinden zusammenkommen.

Im Vorbeitrag habe ich untersucht, ob wir mit rein mathematischen Überlegungen weitere Intervalle finden können, die in realen Tonleitern vorkommen. Dabei finden wir mit wenigen mathematischen Kriterien einen ersten Pool von Intervallen, die sehr «resonanzaffin» sind, d.h. Tonleiter-Ton und Grundton stehen in einem Frequenzverhältnis, das sehr leicht zu einer kräftigen Resonanz führt.

---

Kriterien für Tonleitertöne

1. Tonbereich

Alle mit bekannten Tonleitern bewegen sich im Bereich einer Oktave. Das ist schon verblüffend und wir haben gesehen, dass alle drei Welten am Zustandekommen beteiligt sind.
Entscheidend für die Tonleitertöne sind ihre Frequenzen (f). Dabei kommt es nicht auf die absolute Höhe der Frequenz an, sondern nur auf die relative im Vergleich zu anderen Tönen. In der Folge bezeichnet die 1 den Grundton und die 2 die Oktave davon. Alle Tonleitertöne müssen sich zwischen dem Grundton und der Oktave befinden, mathematisch gesehen bedeutet das für die relative Frequenz f_(TL) des Tonleitertons bezogen auf den Grundton:

1 ≤ f_(TL) ≤ 2

2. Resonanz

Die physikalische Bedingung für Resonanz ist, dass zwei Frequenzen in einem «rationalen» Verhältnis stehen. «Rational» bedeutet in der Zahlentheorie eine Zahl, die als Bruch von zwei ganzen Zahlen geschrieben werden kann. Mit anderen Worten: f₂ = m/n f₁ (m und n sind ganze Zahlen, f₁ und f₂ sind die beiden Frequenzen). Wir stellen nun die Hypothese auf, dass ein Tonleiterton (TL) zum Grundton (GT) vorteilhafterweise in einem Verhältnis (m/n) stehen, in dem sich eine Resonanz entwickeln kann. Mathematisch heisst das:

f_(TL) = m/n f_(GT)

Diese Bedingung hat mit der physikalischen und der mathematischen Welt zu tun und ist unabhängig von unserem subjektiven und kulturellen Empfinden eine generell gültige physikalische Bedingung für Resonanz, auch im nicht-akustischen Bereich.

Wenn das Rechnen mit Intervall-Brüchen für Sie neu ist, empfehle ich Ihnen die Adnexe, in denen die Rechenvorgänge und ihre Hintergründe detailliert beschrieben sind.

3. Kräftige Resonanz

Eine Resonanz entsteht nicht immer gleich schnell und gleich kräftig. Einige Tonleitertöne können deshalb schneller und kräftiger eine Resonanz entwickeln als andere. Ich stelle die Hypothese auf, dass die Resonanz umso stärker ist, je kleiner m und n sind und habe, ausgehend von der Zahl 1, untersucht, was für Intervalle wir mit möglichst kleinen Werten für m und n erhalten.

Überraschenderweise zeigt es sich, dass alle kleinen Nenner bis 5 nur Tonleitertöne ergeben, die wir in unseren traditionellen europäischen Tonleitern finden. Bei der Suche wird auch sichtbar, dass es nicht allein auf die absolute Höhe von m und n ankommt, sondern vielmehr auf die Primzahlen, die bei der Primzahlzerlegung von m und n entstehen. Hier zeigt sich erneut, dass 5 bei den Primzahlen auch für den Zähler die Grenze ist. In diesem Sinn sind 6, 8 und 9 als Nicht-Primzahlen zerlegbar (6=2×3, 8=2x2x2 und 9=3×3) und für Resonanzen brauchbar. Die 7 aber kann als Primzahl nicht weiter zerlegt werden und ist deshalb für m und n in der Praxis bereits zu hoch.

m und n sollen möglichst klein sein, präziser:

Bei der Primzahlzerlegung von m und n soll 5 die höchste Primzahl sein.

Weshalb die Primzahlzerlegung? – Der Tonleiterton steht nicht allein da, d.h. er soll nicht nur eine Resonanz zum Grundton haben, sondern auch zu anderen Tonleitertönen. Dabei entstehen zusammengesetzte Resonanzen (Brüche), bei denen oft in Zähler und Nenner gekürzt werden kann. Dadurch wird aus einer 8 schnell eine 4, aus der 15 eine 3 und wir haben wieder sehr kleine m und n. Beispiele werden folgen.

4. Weitere Kriterien
Die Resonanz ist nicht die einzige Bedingung für attraktive Tonleitern. Musiker und Zuhörer müssen die Töne ja auch unterscheiden können. Das ist einfacher, wenn es nicht zu viele Töne sind und wenn sie nicht zu nahe beieinanderliegen. Dies sind keine mathematischen Bedingungen, sie haben auch nichts mit der Resonanz zu tun. Der Ursprung dieser Forderung an die Tonleiter hat mit unserer Rezeption zu tun, also mit dem was wir wahrnehmen können – also unserer mentalen Welt. Unsere Wahrnehmung stützt sich dabei auf die Physik unseres Innenohrs und die Physik unseres Gehirns. Es handelt bei diesen Kriterien also um eine Forderung aus der mentalen Welt, gestützt auf die physikalische. An der Entstehung der vielen tausend verschiedenen Tonleitern sind offensichtlich alle drei Welten beteiligt. Nicht resonanzbedingten Kriterien sind:

4a)  Die Anzahl der Tonleitertöne darf nicht zu hoch sein.

4b) Die Tonleitertöne dürfen nicht zu nahe beieinander liegen.

Weder die Anzahl der Töne, noch ihr Minimalabstand sind in jeder Kultur gleich. In der Musik gibt es neben der Resonanz weitere Prinzipien, nämlich das der Interferenz und das Höher/Tiefer-Prinzip. Wenn Töne sehr nahe beieinanderliegen, können bei entsprechender Schulung durch die erlebte Kultur gerade sehr engliegende Töne interessant werden. Allerdings geschieht dies nicht über den gesamten Oktav-Umfang der Tonleiter. Denn wenn die Töne sehr nahe beieinanderliegen, darf die Gesamtzahl der Töne in der Leiter trotzdem nicht überhand nehmen. Zwischen anderen Tönen muss dann der Abstand auch wieder einmal grösser sein. Ein Tonleiter mit Vierteltönen über die ganze Oktave ist denkbar, wird sich in der Praxis aber kaum durchsetzen.

Neben den Interferenzen und dem Höher-Tiefer-Prinzip gibt es ein weiteres Prinzip, das Abwechslungs-Prinzip. Dieses ist weder mathematisch noch physikalisch, sondern nur mental begründbar. Wenn nämlich alles gleich ist, z.B. die Abstände in der Tonleiter, dann wird es langweilig. Deshalb empfinden wir z.B. die Ganzton-Tonleiter, welche aus lauter gleichen Intervallen besteht, als nicht besonders spannend. Die gleiche Ganzton-Tonleiter kann aber in einer Mischung mit anderen, variantenreicheren Leitern gerade einen interessanten Kontrast setzen. Musikstücke hingegen, die nur Ganzton-Tonleitern verwenden würden, wären nicht lange interessant.

Wir haben somit ein weiteres nicht-resonanzbedingtes Kriterium:

4c) Die Abstände in der Tonleiter sollen nicht alle gleich sein.

Grundton-Prinzip: Der Grundton ist der Ton, der die Tonleiter zusammenhält. Beim Abschnitt über die Kirchentonarten werden wir näher darauf eingehen. Als Folge des Grundton-Prinzips werden wir die Tonleitertöne stets auf den Grundton beziehen.

4d) Wir vergleichen alle Tonleitertöne über den Grundton.

---

Mit diesen Bedingungen werden wir unseren Pool von Intervallen aus dem Vorbeitrag sichten und erste Tonleitern herausfiltern. Nicht überraschend sind es solche, welche nicht nur mathematisch sehr einfach gebaut sind, sondern weltweit vorkommen. Es handelt sich um gewisse Pentatoniken, die nicht nur rund um den Globus in Reinform gebräuchlich, sondern auch in etwas komplexeren Tonleitern, z.B. unserer Standard-Durtonleiter als Grundgerüst mitenthalten sind. Zuerst schauen wir die resonantesten Tonleitern an

---

Die ist ein Beitrag zur Entstehung der Tonleitern.

---

 

Resonanz funktioniert über gemeinsame Obertöne

Resonanz besteht, wenn zwei schwingungsfähige physikalische Träger gemeinsam schwingen. Dabei kommt es auf die Eigenfrequenz der beiden Träger an:

• Resonanz 1. Grades: Beide Träger schwingen in der gleichen Frequenz (f2 = f1)
• Resonanz 2. Grades: Ein Träger schwingt in einer Obertonfrequenz des anderen (f2 = n * f1)
• Resonanz 3. Grades: Beide Träger schwingen in einer gemeinsamen Obertonfrequenz (f2 = n/m * f1)

Die Resonanz 3. Grades zeigt sich dadurch, dass das Verhältnis der beiden Frequenzen einem Bruch mit ganzen Zahlen (n/m) entspricht. Diese Resonanz 3. Grades ist die, die uns interessiert, denn sie ist für Tonleitern und Akkorde wirksam, und nicht wie oft angenommen diejenige 2. Grades (siehe den diesbezüglichen Vorbeitrag).

Beispiel Quinte

Eine Saite a' habe die Grundfrequenz 440 Hz und eine Saite e" die Frequenz 660 Hz. Dann schwingt auf der Saite a' der zweite Oberton mit 3 x 440 = 1320 Hz und auf der Saite e" der erste Oberton mit der Frequenz 2 x 660 = 1320 Hz. Dieser Ton ist der gemeinsame Oberton.
Die Saite a' kann nun die Saite e" über diesen gemeinsamen Oberton die Saite anregen. Das Verhältnis der beiden Grundfrequenzen ist entsprechend 3/2.

These

Damit Resonanz entsteht, müssen die Frequenzen im Verhältnis eines Bruchs mit ganzen Zahlen sein.

Warum ganze Zahlen?

Im Schwingungsmedium (Saite, Basilarmembran, etc.) entstehen bei einer Schwingung stehende Wellen. Diese sind dadurch charakterisiert, dass die Saite an ihren beiden Enden nicht schwingt, sondern nur in der Mitte, mit einem oder mehreren Bäuchen. Die Zahl der Schwingungsbäuche in der Mitte muss eine ganze Zahl sein, da sonst die stehende Welle an den beiden Enden nicht auf der Nulllinie wäre.

---

Tonleitertöne bewerten anhand der Resonanzen

Oktaven und Quinten lassen sich, wie wir hören können, sehr leicht in Resonanz bringen (Quintenexperiment) und zeichnen sich durch sehr einfache Resonanzverhältnisse (f2/f1) aus, nämlich 2/1 für die Oktave und 3/2 für die Quinte. Mit ganz wenigen mathematischen Bedingungen lassen sich nun weitere Tonleitertöne finden:

Kriterien für die Töne einer Tonleiter

Es wird jeweils das Intervall des Tons zum Grundton der Tonleiter angesehen.

1. Das Intervall muss innerhalb einer Oktave liegen: Das heisst, der Bruch der beiden Frequenzen (Tonleiterton zu Grundton) muss ≥ 1 und  ≤ 2 sein.
2. Das Intervall muss resonanzfähig sein: Nenner und Zähler des Bruchs müssen ganze Zahlen sein.
3. Die Resonanz soll möglichst kräftig sein: Der Nenner des Bruchs soll möglichst klein sein.

Die beiden letzten Kriterien sind entscheidend, aber etwas erklärungsbedürftig und ich werde gerne die Gründe dafür veranschaulichen. Im Moment aber nehme ich alle drei mathematischen Kriterien als gegeben an und schaue, ob wir damit weitere bekannte Intervalle finden können.

---

Generierung eines Pools möglicher Tonleitertöne mit Hilfe dieser drei Kriterien

Wir gehen von den Nennern aus und starten dabei mit den Nennern 1 und 2. Bereits enthalten in unserer Tonleiter sind:

Alle übrigen Töne mit Nenner 1 oder 2 liegen ausserhalb unseres Oktavbereichs (1-2). Wir schauen deshalb, ob sich mit dem Nenner 3 weitere bekannte Intervalle ergeben:

Alle weiteren Brüche mit Nenner 3 liegen ausserhalb unseres Oktavbereichs. Wir fahren deshalb mit dem Nenner 4 weiter:

Alle weiteren Brüche mit Nenner 4 liegen ausserhalb unseres Oktavbereichs. Wir fahren deshalb mit Nenner 5 weiter:

Weitere Brüche mit Nenner 5 liegen ausserhalb unseres Oktavbereichs.

Zwischengedanke

Was hier auffällt ist, dass Brüche mit Zähler 7 bei uns in Europa als Intervalle nicht vorkommen. Meine These ist, dass das damit zu tun hat, dass sieben eine Primzahl ist. Das kann erklären, weshalb 8/5 und 9/5 für uns gewohnte Intervalle sind, obwohl Nenner und Zähler bei diesen Brüchen höher ist als bei 7/5. Acht ist 2x2x2 und Neun ist 3×3. Wir werden später sehen, dass wir zur Beurteilung der Resonanz von mehreren Tönen auch mehrere Intervalle miteinander vergleichen können. Zwei Intervalle vergleichen bedeutet in der Frequenzanalyse, dass der Bruch des einen Intervalls durch den Bruch des anderen geteilt wird. Dabei ist es vorteilhaft, wenn gekürzt werden kann. Bei einer Primzahl besteht diese Möglichkeit nicht, bei Zahlen wie 8 oder 9 ist das Kürzen aber oft möglich, insbesondere wenn wir mit Quinten und Quarten das 2 und das 3 im Nenner haben. Beispiele werden folgen.

Für unsere Generierung resonanter Tonleitertöne folgt aber, dass wir auf 7/4 und 7/5 verzichten – weil die 7 im Zähler eine zu hohe Primzahl ist.

Weiter geht es nun mit Nenner 6:

Der Nenner 6 bringt also keine neuen Töne.

Nenner 7 lassen wir als hohe Primzahl weg und gehen gleich zu Nenner 8:

Mit Nenner 8 gibt es somit zwei neue Intervalle, nämlich die grosse Sekunde (9/8) und die grosse Sept (15/8). Zwar sind bei beiden die Zähler und Nenner recht hoch, doch dafür lassen sich ihre Zähler und Nenner durch 2, 3 und 5 teilen. Dadurch werden die Brüche der Intervalle im Verbund von Tonleitern und Akkorden kürzbar und die Intervalle erweisen sich als resonant.

Damit beenden wir die Tonsuche und stellen unsere Funde in aufsteigender Frequenz zusammen:

Pool der resonanzmässig vorteilhaften Intervalle

Bei unserem Pool fällt folgendes auf:

a) Die meisten bei uns verwendeten Intervalle haben ganz einfache Frequenzverhältnisse.

b) Die Quart ist mit tiefem Nenner und Zähler der «viert-logischste» Tonleiterton. Dieser Ton ist aber nie ein Oberton. Trotzdem macht er Sinn und zwar sowohl in der mathematischen Welt (einfacher Bruch), wie in der physikalischen Welt (einfache Resonanzverhältnisse) wie auch mental (subjektives, musikalisches Hörerlebnis).

c) Kleine Sekunde und Tritonus fehlen in unserem Pool. Diese Töne sind mathematisch keine problemlosen Brüche und klingen entsprechend schärfer. Das ist musikalisch natürlich interessant, doch das Ideal einer problemlosen Resonanz wird mit diesen Intervallen verfehlt. Wir werden später sehen, wie der Tritonus sich unter gewissen Bedingungen trotzdem gut in Resonanzen einfügen lässt, die kleine Sekunde hingegen klingt immer scharf und wird dadurch der eigentliche Leitton in der europäischen Musik.

Doch vorerst belassen wir es bei unserem Pool von zehn Tönen. Das reicht für viele, insbesondere für die global am häufigsten verwendeten Tonleitern. Wir haben gesehen, dass das mathematische Kriterium eines Bruchs mit kleinen ganzen Zahlen ausreicht, diesen Pool von resonanten Tonleitertönen rein rechnerisch zu generieren und ihn auf nur 10 Töne zu beschränken. Alle diese rein mathematisch definierten Tonleitertöne sind für unsere Ohren (mentale Welt) keine Unbekannten.  Das mathematische Kriterium läuft perfekt parallel zu dem, was wir hören.

---

Weitere Zwischengedanken

Mathematiker mögen bekanntlich Primzahlen. In dieser Hinsicht können wir das oben genannte 3. Kriterium (möglichst tiefe Zahlen für Zähler und Nenner) präzisieren:

3. Kriterium präzisiert:

Damit das Intervall im Verbund mit anderen Intervallen gut resonanzfähig ist, soll Zähler und Nenner bei der Primzahlzerlegung möglichst kleine Primzahlen ergeben:

2 ist besser als 3
3 ist besser als 5
5 ist besser als 7
7 ist in der Praxis schon zu gross

Intervalle und Rhythmen

Das ist anders als bei Rhythmen, wo Bruchverhältnisse ebenfalls eine Rolle spielen. Weshalb das dort anders ist, und weshalb Rhythmen mit 7 oder 11 Schlägen gut klingen, lässt sich in der 3-Welten-Theorie plausibel erklären. Mehr dazu später.

Vom Pool zu den Tonleitern

Wir suchen nun nach weiteren Kriterien für attraktive Tonleitern. Der gefundene Pool ist ja noch keine Tonleiter, sondern nur unsere Ausgangslage, um daraus die Töne für verschiedene Tonleitern zusammen zu stellen. Dabei gelten weitere Kriterien.

Weitere Kriterien

4. Kriterium: Die Tonleitertöne sollen bevorzugt auch untereinander Resonanzen eingehen können

5. Kriterium: Die Tonleiter hat einen Grundton (eine sogenannte Tonalität), die in der Tonleiter eine ganz besondere Funktion hat.

6. Kriterium: Die Tonleitertöne dürfen nicht zu nahe beieinander sein, sonst können wir sie als Menschen (Laien) nicht mehr unterscheiden. Dies ist ein praktischer Constraint aus der mentalen Welt. In einer rein mathematischen Welt wären beliebige Differenzierungen denkbar, in der Realsituation ist das nicht der Fall.

Mehr zu den Kriterien für Tonleitern im Fortsetzungsbeitrag.

---

Dies ist ein Beitrag zur Entstehung der Tonleitern 

---

 

Für unsere Resonanzüberlegungen spielen Sinusschwingungen eine entscheidende Rolle. Ich möchte auf dieser Seite die Begriffe, die ich dabei verwende, erklären.

Schwingung

Eine Schwingung ist eine Bewegung in der Zeit, die um eine Nulllinie herum pendelt.

Die Schwingung kann verschiedene Formen haben. Für unsere Resonanzüberlegungen gehen wir von reinen Sinusschwingungen aus, eine solche Schwingung zeigt die Abbildung.

Amplitude

Die Amplitude ist die Abweichung der Schwingung von der Nulllinie. Für unsere Überlegungen spielt sie primär keine Rolle.

Periode

Eine Periode dauert so lange, bis die Schwingung wieder am gleichen Ort ist und sich daraufhin genau gleich wiederholt. Je nach Form der Schwingung erfolgen pro Periode zwei oder mehr Nullliniendurchgänge, bei der Sinusschwingung sind es zwei in jeweils gegensätzlicher Richtung.

Wellenlänge

Die Wellenlänge ist die Länge einer Periode.

Frequenz

Die Frequenz bezeichnet die Anzahl der Perioden pro Zeiteinheit. Sie ist für unsere Resonanzüberlegungen die entscheidende Grösse, denn während Amplituden und Wellenlängen je nach Trägermedium der Welle wechseln, bleibt die Frequenz bei einer Schwingungsübertragung von einem Medium zum anderen erhalten.

«Bauch»

Pro Periode hat die Sinusschwingung einen Bauch in die positive und einen in die negative Richtung. Wenn wir die Bäuche pro Zeiteinheit zählen, messen wir damit die Frequenz. Das „Bauchzählen“ misst also die Frequenz. Der saloppe Ausdruck hat den Vorteil der Anschaulichkeit. Gleichzeitig betont der Ausdruck «Bauch» die Unteilbarkeit (mathematisch: ganze Zahlen!), während die Frequenz mit beliebigen reellen Zahlen angegeben werden kann.
Für die Resonanzverhältnisse werden immer ganze Zahlen, also die Zahl der vollendeten Bäuche, verglichen. Ob man nur die positiven oder sowohl positive wie negative Bäuche zählt, ist irrelevant, da beim Frequenzvergleich in beiden Fällen durch Kürzen die jeweils gleichen Quotienten (Brüche) entstehen.

Eigenfrequenz

Gewisse physikalische Medien (Saiten, Luftsäulen in Pfeifen, etc) haben die Eigenheit, in einer ganz bestimmten Frequenz zu schwingen, in ihrer Eigenfrequenz.

Grundton und Obertöne

Neben der Eigenfrequenz als Grundfrequenz (Grundton) kann das Medium auch mit einem ganzzahligen Vielfachen dieser Grundfrequenz schwingen. Ganzzahlig meint hier: Es kommt auf die Zahl der ganzen Perioden (Bäuche) an.

Die Quinte

Schauen wir als erstes die Quinte an. Sie kommt in praktisch allen Tonleitern der menschlichen Kulturen vor. Tonleitern ohne diese reine Quinte existieren, doch diese Tonleitern erscheinen mir einerseits künstlich und bewusst konstruierte wie die Ganztonleiter zu sein, oder dann eher ungebräuchliche, wie das Lokrische. Die Bluestonleiter, die mit dem «Blueston», d.h. der «Flat Five», einen Ton knapp neben der Quinte benützt, kennt neben dieser verminderten Quinte (=Flat Five) auch die ganz normale Quinte. Die Quinte ist sicher nach der Oktave das Intervall, das am häufigsten in all den Tausenden von Tonleitern auf dieser Erde vorkommt.

Quinte und Duodezime

Kann diese normale Quinte wie die Oktave durch Resonanz entstehen? Sie ist zwar kein direkter Oberton, doch sie kann trotzdem über die Obertöne erreicht werden. Ich zeige hier gleich wie das funktioniert, nämlich über einen kurzen Umweg über die Duodezime, den dritten Oberton.

Zur Veranschaulichung zeige ich hier nochmals die Abbildung mit den schwingenden Obertönen:

Abb. 1: eine schwingende Saite mit Grundton und den ersten vier Obertönen

In Abb. 1 habe ich den dritten Oberton sogar schon als Quinte bezeichnet, eigentlich falsch, denn es ist in Wirklichkeit eine Duodezime. Trotzdem erscheint uns dieser Ton beim Hören sofort als eine Quinte. In Abb. 2 sehen Sie ein Beispiel für Quinten und Duodezimen auf dem Klavier:

Abb 2: Oktave und Duodezime auf dem Klavier

In unserem Beispiel ist der Grundton ein (grosses) C. Der erste Oberton, die Oktave, ist ein (kleines) c und der zweite Oberton, die Duodezime ein (kleines) g. Bekanntlich sind Intervalle immer relativ. Dieses kleine g ist nun bezogen auf den Grundton C zwar eine Duodezime, aber bezogen auf den ersten Oberton, nämlich auf das kleine c, ist das g eine Quinte.

Die Frequenz der Quinte

Wie steht es nun um dieses Intervall c-g frequenzmässig? Vergleichen wir dazu Abbildung 1 und 2: Der Ton 3 von Abb. 1 (g) ist das 3-fache der Grundschwingung (C) und der Ton 2 (c) das 2-fache. Somit schwingt Ton 3 (g) bezogen auf Ton 2 (c) 3/2 mal so schnell. Wenn wir also nicht das grosse, sondern das (kleine) c als Grundton nehmen, dann ist das (kleine) g die Quinte. Und in der Quinte schwingt der obere Ton (das g) 3/2 mal so schnell wie der untere Ton (das c). Das gilt ganz allgemein: Ein Ton der 3/2 mal so schnell schwingt wie ein anderer, klingt für uns eine Quinte höher.

Die drei Welten in der Quinte

Der Bruch 3/2 ist die mathematische Seite der Quinte. Wir haben sie über die Physik der Saitenschwingungen hergeleitet. Gleichzeitig haben wir die bereits erwähnten Bedingungen (Constraints) aus der mentalen Welt eingehalten: Die Quinte – wenn sie ein Tonleiterton sein soll – darf nämlich nicht zu weit weg vom Grundton sein. Das gilt für jeden Tonleiterton, er muss sich innerhalb einer Oktave bewegen. Mathematisch bedeutet das, dass das Verhältnis seiner Frequenz zur Frequenz des Grundtons zwischen 1 (=Grundton) und 2 (=Oktave) liegen muss. Die Quinte erfüllt das mit dem Frequenzverhältnis 3/2 = 1.5. Bei der Duodezime ist das Frequenzverhältnis 3, also grösser als 2 und somit ist die Duodezime kein Tonleiterton. Wir empfinden sie als Quinte, einfach eine Oktave höher, aber wie erwähnt, in der mentalen Welt empfinden wir die Oktave als den «gleichen» Ton.

Das Resonanzexperiment zur Quinte

Für den Bezug von Grundton, Quinte und Duodezime schlage ich Ihnen ein weiteres Resonanzexperiment auf dem Klavier vor:

Abb 3: Resonanzexperiment für die Quinte. Im Vergleich zu Abb. 2 ist nun die Quinte – das grosse G – und nicht das kleine g die Taste, auf der wir die Resonanz untersuchen.

Als erstes testen wir erneut die Duodezime und drücken wie beim Oktavexperiment mit der rechten Hand die Taste der Duodezime (das kleine g). Dabei soll die Saite nicht klingen, aber die Taste heruntergedrückt bleiben. Mit der linken Hand schlagen wir kurz und kräftig auf das C, also den Grundton. Wie beim Oktavexperiment sollte nun die heruntergedrückte Saite (g) klingen, obwohl sie nicht angeschlagen wurde. Es handelt sich um eine reine Resonanz, die Saite klingt, weil sie durch Schallwellen angeregt worden ist. Das funktioniert, weil das kleine g ein Oberton des grossen C ist.

Was aber ist mit dem grossen G, also der Quinte? Halten Sie zum Test das grosse G lautlos heruntergedrückt  und schlagen dabei kräftig den Grundton an, also das grosse C. Sie hören nun einen hohen Ton. Wenn Sie genau hinhören, werden Sie feststellen, dass es sich nicht um die Quinte, also das grosse G handelt, sondern um die Duodezime, nämlich das kleine g. Wie kommt das, das dieser Ton erklingt, wo Sie doch die Taste des kleinen g’s gar nicht heruntergedrückt halten?

Effektiv erklingt das kleine g auf der Saite des grossen G’s! Das heisst die Saite schwingt nicht in ihrer Grundschwingung, sondern in ihrer ersten Oberschwingung, der Oktave. Das geht gut, denn die Saite kann mit zwei Bäuchen fast so gut schwingen wie mit einem. Es handelt sich um einen sogenannten Flageolett-Ton.

Mit anderen Worten: Sie haben auf der Saite G eine Oberschwingung angeregt, deren Frequenz doppelt so schnell wie die Grundfrequenz der Saite ist. Woher aber wurde die Frequenz angeregt? – Es ist die gross C Saite, welche den Oberton initiiert hat. Auch bei der Schwingung dieser C-Saite ist ja das kleine g als Oberschwingung  enthalten, nämlich als 2 Oberton. Dieser 2. Oberton regt nun die (gross) G Saite zur Resonanz an, aber nicht in ihrer Grundschwingung, sondern in ihrem ersten Oberton, dem kleinen g. Denn nur dieses ist als Oberschwingung auf der (gross) G Saite anregbar. Diesen Ton (g) hören Sie auf der (G)-Saite, solange Sie die G-Taste gedrückt halten.

Tabelle 1: Die Resonanz in der Quinte

Die Resonanz erfolgt bei der Quinte somit über den Umweg der Obertöne.  Keine Saite ist in ihrer Grundschwingung beteiligt, sondern beide Saiten nur über ihre Oberschwingungen. Dass das funktioniert, haben Sie mit dem Quintenexperiment gezeigt.

Die Quinte, ein einfacher Bruch

In Tabelle 1 wird die Quinte als Bruch dargestellt: 3/2.

Wie wir gesehen haben, müssen alle Tonleitertöne im Bereich einer Oktave sein, das heisst ihre Frequenz muss zwischen dem Einfachen und dem Doppelten der Frequenz des Grundtons sein. Das haben wir mit dem Frequenzverhältnis 3/2 = 1.5 erreicht. Wir haben damit den ersten Ton innerhalb des Oktavbereichs  gefunden, der ein sehr einfaches Intervallverhältnis zum Grundton hat. Während die Oktave doppelt so schnell schwingt wie der Grundton, schwingt die Quinte 3/2 mal so schnell.

Die Obertöne kommen mit Ausnahme der Oktave für die Tonleitern nicht infrage. Sie können spielen aber trotzdem als Überträger der Resonanz eine Rolle. Wir haben die Quinte erhalten, indem wir die Duodezime (2. Oberton) einfach um eine Oktave herunter gebrochen haben. Dieses Herunterbrechen um eine Oktave zeigt sich als die 2 im Nenner. Die 3 im Zähler ist das «Erbe» des zweiten Obertons, der Duodezime, die dreimal so schnell schwingt wie der Grundton..

Ausblick

Mit dem Bruch 3/2, der die Quinte definiert, haben wir ein auffällig einfaches Zahlenverhältnis erhalten. Das ist kein Zufall. Wir werden sehen, wie diese einfachen Zahlenverhältnisse (ideale Welt) auch für die anderen Tonleitertöne eine Rolle spielen. Gleichzeitig werden wir sehen, dass das Kochbuch für diese Töne zuerst sehr mathematisch erscheint, dann aber durch die Constraints der physikalischen und mentalen Welt zunehmend gebrochen wird und schliesslich zu der scheinbar unendlichen Vielfalt an unterschiedlichen Tonleitern führt.

Schon die Tatsache, dass wir nicht mehr einfache ganzzahlige Verhältnisse wie bei den Obertönen für die Tonleitern verwenden können, sondern dass jetzt Brüche (mit ganzen Zahlen) verwendet werden, ist dem Constraint der Oktavbeschränkung geschuldet, die ein Constraint der physikalisch/mentalen Welt ist. Wir werden weitere Constraints finden – aber auch sehen und hören, wie die drei Welten immer wieder ganz nah zusammen kommen, fast so nah wie bei der Oktave.

---

Die Quinte ist nicht der einzige Bruch unter unseren Tonleiterintervallen. Ganzzahlige Brüche definieren die wichtigsten Tonintervalle. Mit einer einfachen Konstruktionsregel finden wir sie. Auf einem Fortsetzungbeitrag erkläre ich das Prinzip, das auf bemerkenswerte Weise Mathematik, Physik und menschliches Empfinden zusammenbringt.

---

Dies ist ein Beitrag zur Entstehung der Tonleitern

---

 

Dies ist ein Beitrag zur Entstehung der Tonleitern und setzt den Beitrag zur Wahrnehmung der Oktave fort.

Funktioniert das Zusammentreffen der drei Welten nur für die Oktave?

Die Oktave zeigt, wie mit der mathematisch organisierten Obertonreihe die Mathematik, also die ideale (Penrose: platonische) Welt in die physikalische Welt eintritt und wie dieses Zusammentreffen von Mathematik (ganze Zahlen) und Physik (schwingende Materie) ein ganz spezielles Phänomen ermöglicht, nämlich die Resonanz. Die Resonanz wiederum nehmen wir Menschen subjektiv (Penrose: mentale Welt) als etwas ganz besonderes wahr. Zwei Töne im Abstand von einer Oktave erkennen wir subjektiv als gleiche Töne. Jedem von uns erscheint – unabhängig von der kulturellen Prägung – ein Ton mit der doppelten Frequenz als der «gleiche» Ton (Happy-Birthday-Experiment).

Wenn das Frequenzverhältnis (Mathematik) nur ein bisschen abweicht, verschwindet die Resonanz (Physik) und die Töne erscheinen uns (mental) als verschieden, ihr gemeinsames Erklingen als ein Missklang.

Bei der Oktave als erstem Oberton verbinden sich also die drei Welten. Können wir die auf die Oktave folgenden weiteren Obertöne ebenfalls für unsere Tonleiter verwenden? Die Antwort auf diese Frage ist kein einfaches Ja, denn die mathematische Reihe der ganzen Zahlen muss sich in die Sachzwänge der physikalischen und der mentalen Welt einfügen.

Was sind das für Zwänge? Und ist die Obertonreihe überhaupt eine Tonleiter, die in der Praxis Sinn macht?

Sachzwänge (Constraints) in der physikalisch / mentalen Welt
Töne dienen der Kommunikation und Säugetiere und Menschen kommunizieren akustisch. Sie sind fähig, Laute zu produzieren und sie zu hören. Diese physikalisch/mentale Gegebenheiten der Kommunikation müssen wir berücksichtigen, wenn wir uns überlegen, wie die Tonleitern entstanden sind.

Wir können nämlich mit unserer Stimme nicht Tonhöhen beliebiger Frequenz produzieren. Und wenn zwei Töne von ihrer Frequenz sehr weit auseinander sind, können wir schlecht ihren gegenseitigen Abstand messen (mentale, subjektive Welt). Deshalb dürfen die Töne einer Tonleiter nicht zu weit voneinander entfernt sein. Dies ist der erste Sachzwang der physikalischen und mentalen Welt bei der Bildung von Tonleitern.

Diese physikalisch/mentale Einschränkung kann noch weiter begründet und präzisiert werden: Weil wir einen zweiten Ton eine Oktave höher als den «gleichen» Ton wahrnehmen (Happy-Birthday-Experiment), darf eine Tonleiter den Bereich einer Oktave nicht überschreiten. Es gäbe sonst eine Überschneidung der Tonleiter mit sich selber, weil Töne ausserhalb der Oktave innerhalb der Oktave sofort einen «gleichen» Ton finden.  Aus diesem Grund ist eine Tonleiter immer auf den Bereich einer Oktave beschränkt, genau so wie wir es in allen Musikkulturen auch feststellen können.

Die Töne dürfen andererseits auch nicht zu nah beisammen sein, denn dann können wir sie nicht mehr unterscheiden. Die Tonleitertöne dürfen aus diesem Grund nicht beliebig viele Töne haben – auch wenn dies mathematisch durchaus denkbar wäre. Doch nicht alles, was mathematisch möglich ist, macht in der Realität Sinn.

Die Folgen aus diesen Bedingungen für Tonleitern lassen sich in zwei Punkten zusammenfassen:

1. Die Töne der Leiter dürfen sich nur im Raum einer Oktave bewegen.
2. Es dürfen nicht zu viele Töne in der Tonleiter vorkommen.

Dies ist das physikalisch/mentale Constraint für Tonleitern.

---

Wie können nun unter diesen Constraints überzeugende Tonleitern entstehen? Können das weiterhin solche sein, die einfache mathematische Verhältnisse aufweisen?  → siehe Folgebeitrag.

---

Dies ist ein Beitrag zur  Entstehung der Tonleitern

---