Schlagwort-Archive: Drei-Welten-Theorie

Drei-Welten-Theorie

Tonleitern

Sind unsere Tonleitern erklärbar?

Obwohl es tausende von verschiedenen Tonleitern gibt, haben alle gewisse Gemeinsamkeiten. Woher kommen diese Gemeinsamkeiten und wie sind die Tonleitern überhaupt entstanden?

Drei-Welten-Theorie

Auf das Thema der Tonleitern bin ich über die Drei-Welten-Theorie nach Roger Penrose gestossen. Der Nobelpreisträger Penrose bewegt sich sowohl in der Mathematik wie der Physik. Doch  er denkt auch darüber nach, wie er nachdenkt.

Die drei Welten sind:

Selbstreferentialität und Logik

Das Nachdenken über das Nachdenken ist ein typsicher selbstreferentieller Prozess, der eine grosse Herausforderung für die Logik darstellt.

Das hat auch sehr viel mit unserem Selbstverständnis als Menschen zu tun und mit der Logik, mit der wir die Natur erklären. Auf dieser Website finden Sie weitere Beiträge genau zu diesen Themen.

Appendix
Drei-Welten-Theorie, Semantik

Mentale Welt

Hinterlassen Sie einen Kommentar

Was ist die mentale Welt?

Die mentale Welt ist die Welt in unserem Kopf. Es ist die Weise, wie wir die Welt wahrnehmen, sie umfasst unsere Empfindungen, Gefühle und Gedanken. Es ist eine ganz subjektive Welt.

In der Drei-Welten-Theorie ist die mentale Welt die dritte neben der physikalischen und die platonischen.

Unterschied zur physikalischen Welt

Während die physikalische Welt objektiv fassbar ist, bleibt die mentale subjektiv.

Mit anderen Worten: Während wir die Gegenstände der physikalischen Welt von aussen beobachten können, ist dies mit den Gegenständen der mentalen Welt nicht möglich.

Beispiel Farbe

Objektiv (physikalisch) sind die Farben messbar als Wellenlängen von Lichtwellen. So hat z.B. gelb oder blau eine bestimmte Wellenlänge, die in Nanometern objektiv messbar ist. Was wir wahrnehmen ist allerdings nicht die Wellenlänge. Wir haben einen subjektiven Eindruck von Gelb oder Blau, der zwar durch das physikalische Phänomen der Lichtwelle ausgelöst wird, doch was wir empfinden ist nicht die Wellenlänge, sondern ein ganz subjektiver Eindruck von gelber oder grüner Farbe. So nehmen wir z.B. grün als eine bestimmte Farbe wahr, die einem bestimmten Wellenlänge entspricht. Wie wir aus dem Zeichnungsunterricht wissen, kann das Grün aber aus blau und gelb gemischt werden. Das heisst, was auf unser Auge physikalisch eintrifft, ist eine Kombination von Photonen mit ‹blauer› und ‹gelber› Wellenlänge. Wir nehmen aber nicht diese beiden objektiv vorhandenen Wellenlängen wahr, sondern wir eimpfinden die Kombination als Grün, also als eine ganz andere Wellenlänge. Dieser subjektive Eindruck wird in der Literatur ‹Qualia‹ genannt.

Existiert die mentale Welt wirklich?

Oder ist sie einfach eine Auswirkung (Emanation) der physikalischen Welt? Viele Leute glauben dies. Der subjektive Eindruck, den wir empfinden, wird im Gehirn durch die elektrische Ströme erzeugt, die die Photonen auf unserer Netzhaut auslösen. In diesem Sinn existiert die mentale Welt nicht wirklich, sondern ist eine Emanation der physikalischen Welt, eine blosse Auswirkung der Physik, die uns die Farbempfindung vortäuscht.

Am anderen Ende des Spektrums stehen die Solipsisten und die radikalen Konstruktivisten wie Ernst von Glasersfeld. Für Solipsisten ist die mentale Welt – also ihre eigene Vorstellung – die einzige Welt, die sicher existiert. Alles andere kann eine Täuschung sein, ein Traum, nur die eigene Vorstellung ist sicher.

Wir haben also zwei Extreme

a) Physikalisten: Nur die physikalische Welt e xistiert, die mentale Welt wird völlig durch die physikalische konstruiert.

b) Solipsisten: Nur die mentale Welt existiert, sie täuscht uns die Existenz einer physikalischen Aussenwelt vor.

Interessanter als diese beiden Extreme sind die Meinungen dazwischen. Roger Penrose z.B. plädiert mit seiner Drei-Welten-Theorie dafür, keine der drei Welten als nicht-existierend auszuschliessen. Es geht ihm vielmehr darum, die Beziehungen der drei Welten zu klären.

Koexistenz

Dies ist auch meine Haltung: Obwohl es plausibel erscheint, die mentalen Empfindungen und Vorgänge als reine Auswirkungen der physikalsichen Welt zu sehen, erscheint es mir sinnvoll, die mentale Welt als eigene Welt anzusehen. Nicht weil sie nicht aus der physikalischen emaniert sein könnte, sondern weil sie auf diese Weise besser beschrieben werden kann. Um auf das Beispiel der Farben zurückzukommen: Es ist für das menschliche Verhalten irrelevant, ob grün mit seiner korrekten eigenen Wellenlänge oder mit einer Kombination von gelben und blauen Wellenlängen erzeugt wird, ich sehe immer die gleiche Farbe und verhalte mich auch entsprechend. Die Beschreibung des menschlichen Denkens, Empfindens und Verhaltens wird einfacher und gleichzeitig präziser, wenn wir die Vorgänge in der mentalen Welt direkt angehen. Dies ist möglich, aber nur von innen, wenn ich mir die Gedanken, Farben etc. der mentalen Welt selber vorstelle.

Auch eine Kommunikation über mentale Gegenstände (Gedanken, Farben etc.) ist möglich, setzt aber ebenfalls eine subjektiven Erfahrungsgrundlage voraus, diesmal eine, welche die Kommunikationsteilnehmer auf ähnliche Weise erlebt haben.

Wo spielt die mentale Welt eine Rolle?

Überall, wo es im innere Wahrnehmungen und Vorgänge geht, sind wir in der mentalen Welt.

Folgende Gebiete lassen sich kaum beschreiben, ohne die Existenz der mentalen Welt zu akzeptieren:

  • Psychologie
  • Kultur
  • Werte, Moral
  • Politik
  • Kunst

Die mentale Welt ist somit nicht ganz irrelevant.

Semantik

In meinem eigenen Gebiet, der Semantik, ist eine klare Trennlinie zwischen der objektiven und der subjektiven Welt erkennbar. Während Wörter und Sätze Teil der objektiven Welt sind, sind die Begriffe, also die Bedeutungen der Wörter, und die Gedanken, die mit den Sätzen ausgedrückt werden, Teil der subjektiven, d.h. der mentalen Welt.

Dies ist ein Beitrag zur Drei-Welten-Theorie.

Drei-Welten-Theorie

Was ist Resonanz?

Hinterlassen Sie einen Kommentar

Die physikalische Basis der Resonanz

Resonanz basiert auf den Eigenschwingungen von physikalischen Medien und ihrer gegenseitigen Koppelung.

Koppelung der Eigenschwingungen von physikalischen Objekten

Die Eigenschwingungen sind stehende Wellen, deren Frequenz von den Eigenschaften des physikalischen Mediums (Grösse, Form, Material, etc. ) bestimmt wird.

Zwei solche Medien können über ihre Eigenschwingung in eine  Resonanz treten. Die Resonanz entsteht durch eine Koppelung der beiden Eigenschwingungen, sodass die beiden physikalischen Medien in ihrem Schwingungsverhalten eine gekoppelte Einheit bilden.

Die Koppelung erfolgt über einen physikalischen Energieaustausch, sei es direkt oder indirekt, z.B. über die Luft. Bedingung für das Entstehen der Koppelung ist, dass die Frequenzen der Eigenschwingungen der beiden beteiligten physikalischen Medien in einem dafür geeigneten mathematischen Verhältnis stehen.

Stabilität der Resonanz über die Zeit

Sobald der Resonanzzustand eingetreten ist, bleibt er eine gewisse Zeitspanne stabil, d.h. der gekoppelte Schwingungszustand bleibt stationär, oft über eine längere Zeit. Dieses erstaunliche Verhalten hat mit den Energieverhältnissen zu tun, die bei der Koppelung besonders energiegünstig sind.

Resonante Eigenschwingungen

Auch die Eigenschwingung eines einzelnen physikalischen Objekts kann als Resonanz bezeichnet werden. So weist z.B. ein Elektron um den Atomkern eine Resonanz mit sich selber auf und kann dadurch nur ganz bestimmte Umlauffrequenzen annehmen, die es ihm erlauben, auf seiner Umlaufbahn mit sich selber resonant zu sein. Das Gleiche gilt für das Schwingungsverhalten einer Saite.

Resonanz als Abstraktion

Das physikalische Material bestimmt zwar die Eigenfrequenz der beteiligten schwingenden Medien, doch der Rest, d.h. das Entstehen der gekoppelten Resonanz, ergibt sich aus dem geeigneten Verhältnis der beiden Frequenzen. Dieses Frequenzverhältnis folgt mathematischen Regeln. Eine verblüffend einfache Mathematik reicht aus, zu erkennen, wie stark die Resonanz zwischen den beiden schwingenden physikalischen Medien sein wird.

Drei Welten, nach Roger Penrose

Die Entstehung der Resonanz zeigt eindrücklich das Zusammenspiel von zwei der drei Welten, die gemäss Nobelpreisträger Roger Penrose unsere Realität bilden, nämlich der physikalischen und der platonischen. Letzerer Begriff bezeichnet die abstrakte Welt der Ideen, zu der die Mathematik gehört. Mit der Verwendung des Begriffs ‹platonisch› für die Welt der Mathematik verweist Sir Roger auf die europäische Kulturgeschichte, hier gehört die Diskussion um die Wirklichkeit und Wirksamkeit von Ideen nicht nur zur Philosophie von Platon, sondern bestimmte auch im Mittelalter als Universaliendisput grosse Teile des philosophischen Diskurses. Die Frage hat seither nichts an Relevanz verloren: Wie real sind Ideen? Warum setzt sich Abstraktes in der materiellen Welt durch? Wie ist das Verhältnis von abstrakter Idee und konkreter, d.h. physikalischer Welt?

Ich dachte vor gut einem Jahr, dass das Entstehen der Resonanz in der Musik ein gutes Beispiel wäre, um das Verhältnis von Physik, Mathematik und der dritten Welt, unserem subjektiven Empfinden zu erkunden. Ich war überrascht, wie verblüffend klar der Bezug der drei Welten hier dargestellt werden kann und wie verblüffend einfach, logisch und weitreichend die Mathematik in den Harmonien unserer Musik ist.

Resonanz in der Musik

In einem Musikstück ändern die entstehenden Resonanzen zwischen den Tönen immer wieder und bieten so einen faszinierenden Farbwechsel. Wir können ihn intuitiv erleben, aber auch rational erklären, eben als ein Spiel der Resonanzen unter den Tönen.

Nur die Obertonreihe?

In der Schule habe ich gelernt, dass die Obertonreihe unsere Tonleitern bestimmt. Doch das ist eine grobe Vereinfachung. Das Phänomen der Resonanz kann unsere Tonleitern viel einfacher und direkter erklären als es die Obertonreihe kann. Die Obertonreihe beschreibt das Schwingungsverhalten nämlich nur innerhalb eines physikalischen Medium – die in der Musik interessierende Resonanz entsteht jedoch immer zwischen mindestens zwei verschiedenen Medien (Tönen). Für die Resonanzüberlegungen von zwei Tönen müssen wir konsequenterweise auch zwei Obertonreihen vergleichen. Erst das Nebeneinanderlegen der beiden Reihen erklärt das Geschehen – ein Fakt, der in den Lehrbüchern meist übergangen wird.

Akkorde bestehen aus drei oder mehr Tönen. Auch hier kann die Resonanzanalyse der drei oder mehr beteiligten Töne die Akkordwirkung verblüffend einfach erklären. Nur müssen diesmal nicht die Frequenzen von zwei, sondern von mehreren Tönen gleichzeitig berücksichtigt werden.

Reine und temperierte Stimmung

In Europa hat sich im Barock die gleichmässig temperierte Stimmung durchgesetzt, welche die kompositorischen Möglichkeiten vielfältig erweitert. Das erste, was der Laie zur Theorie der Tonleitern findet, ist deshalb eine genaue Beschreibung der Abweichungen der temperierten von der reinen Stimmung – doch diese Abweichungen sind für die Entstehung von Resonanzen nur von marginaler Bedeutung. Die reine Stimmung ist keine Bedingung für Resonanz, die hier vorgestellte Mathematik der Resonanz erklärt das Phänomen präzis auch bei temperierter Stimmung.

Dies ist ein Beitrag zur Drei-Welten-Theorie nach Penrose und der Herkunft der Tonleitern.

Drei-Welten-Theorie

Was bringt die gleichstufige Temperierung?

Hinterlassen Sie einen Kommentar

Die temperierte Stimmung hat sich in der unserer abendländischen Musikkultur durchgesetzt – trotz des offensichtlichen Nachteils, dass ihre Intervalle nicht mehr rein sind. Das war nur möglich, weil gewichtige Vorteile den Makel der Unreinheit wettgemacht haben:

1. Eine einzige Stimmung reicht für alle Tonarten: der Grundton ist frei wählbar.

Im Prinzip muss bei der reinen Stimmung für jede Tonart und jeden Grundton neu gestimmt werden. Bei einem Cembalo sind das einige Saiten und bei einer Orgel ist das wirklich eine grosse Aufgabe in Anbetracht der vielen Register und Pfeifen. Je weiter die Tonarten voneinander entfernt sind – d.h. je mehr Kreuze und B’s Sie haben – umso schlimmer wird die Verstimmung. Das ändert sich bei der gleichstufig temperierten Stimmung. Sie ist zwar nie ganz rein, doch auch nie so verstimmt wie eine entfernte Tonart. Mit der gleichstufigen Temperierung kann ohne Neustimmen sofort in jeder Tonart gespielt werden. Orgeln, Streicher und Bläser, alle Instrumente können jetzt in allen Tonarten miteinander zusammenspielen.

2. Freies Modulieren

Dieser Vorteil ist besonders offensichtlich und wirkungsvoll. Im gleichen Musikstück können wir nun – ganz ohne Pause und Neustimmen – von einer Tonart beliebig in eine beliebige andere wechseln (modulieren). Mit der reinen Stimmung ist das nur ganz begrenzt für eng verwandte Tonarten möglich. Mit der gleichstufigen Temperierung gibt es für das Modulieren jedoch keine Grenzen mehr.

3. «Geschenkte» Tonarten: 

Mit den sieben Töne der Dur-Tonleiter kann nicht nur Dur gespielt werden. Auf den weissen Tasten des Klaviers können Sie alle Kirchentonarten spielen werden, je nachdem welchern der sieben Töne Sie als Grundton wählen:

C: Ionisch = Dur
D: Dorisch
E: Phrygisch
F: Lydisch
G: Mixolydisch
A: Äolisch
H: Lokrisch

Die C-Dur Tonleiter besteht aus einem bestimmten Wechsel von Ganztönen und Halbtönen. Wenn Sie auf einem anderen Ton als C beginnen, erhalten Sie ein anderes Muster der Ganz- und Halbtöne. Mit den gleichen sieben Tönen können Sie somit je nach Ausgangspunkt sieben in ihrem Muster von Ganz- und Halbtönen verschiedene und damit auch in ihrem Charakter sehr unterschiedliche Tonleitern spielen. Das geht aber nur wenn jeder Ganzton und jeder Halbton jeweils immer gleich gross ist – bei der reinen Stimmung ist das wie gezeigt genau nicht der Fall, bei der gleichstufigen Temperierung aber per definitionem so. Deshalb entstehen aus jeder Heptatonik in der gleichstufigen Temperierung automatisch sieben in ihrem Charakter sehr unterschiedliche Heptatoniken.

Das gleiche gilt für die Pentatoniken: Wenn Sie z.B. auf dem Klavier nur die schwarzen Tasten drücken, spielen Sie automatisch pentatonisch (Penta = Fünf → fünf schwarze Tasten). Je nachdem, welchen Ton Sie als Grundton wählen, spielen Sie eine andere Pentatonik, z.B. die Durpentatonik (mit Fis als Grundton) oder die Mollpentatonik (mit Es als Grundton).

Dieses Prinzip gilt nicht nur für die weissen und schwarzen Tasten, sondern auch für weitere Tonleitern, z.B. das «melodisch Moll» im Jazz. Es handelt sich wie bei Dur und den Kirchentonarten um eine Selektion von sieben Tönen, also eine Heptatonik, allerdings in Abständen, die nicht allein mit den weissen Tasten gespielt werden können. Aber auch bei den «melodisch-Moll» Tonleitern können wir mit einer Auswahl von sieben Tönen sieben charakterlich und funktional sehr unterschiedliche Tonleitern spielen, je nachdem, welchen der sieben Töne wir als Grundton wählen.

4. Polytonalität

Dieses Stilmittel entstand im 20. Jahrhundert mit Strawinsky und anderen Komponisten und ist auch im modernen Jazz gebräuchlich. Dabei werden mehrere Tonarten gemischt, in der Praxis sind es meist zwei (=Bitonalität). Das erscheint auf den ersten Blick etwas gewagt, klingt aber unter entsprechender Beachtung der Resonanzen (!) – durchaus eingängig.

Fazit aus Sicht der Drei-Welten-Theorie

Die mathematische Reinheit (platonische Welt) der Intervallresonanzen wird durch die Temperierung verletzt, aber so minimal, dass die resultierenden Schwingungsphänomene (physikalische Welt) sich trotzdem einstellen und das Hörerlebnis (mentale Welt) kaum geschmälert wird.

Andererseits werden aber durch das freie Modulieren die Kombinationsmöglichkeiten der insgesamt immer noch nur zwölf Töne gewaltig erweitert. Diese mathematische Erweiterung (platonische Welt) ist hörbar und spannend (mentale Welt). Durch die minimale Unreinheit gewinnt die Musik an Varianten und Reichtum.

Die ist ein Beitrag zur Entstehung der Tonleitern.

 

Drei-Welten-Theorie

Weshalb Resonanz auch bei Unschärfe funktioniert

Hinterlassen Sie einen Kommentar

Wann entsteht Resonanz?

Resonanz zwischen zwei physikalischen Medien hängt vom Frequenzverhältnis ihrer Eigenschwingungen ab. Wenn die beiden Frequenzen einen einfachen Bruch bilden, z.B. 2/1 oder 3/2, kann Resonanz entstehen. In einem früheren Beitrag  habe ich dargestellt, wie die zehn einfachste Frequenzverhältnisse mathematisch zwingend genau zu den zehn Tönen führen, die in unseren Tonleitern vorkommen, seien es Dur, die verschiedene Molltonleitern, Kirchentonarten, Durpentatonik, Mollpentatonik, Bluestonleiter etc..

Reine und temperierte Stimmung

Funktioniert die Resonanz aber auch in der gleichstufig temperierten Stimmung? Im Beitrag zur gleichstufigen Stimmung haben wir gesehen, wie sich die beiden Stimmungen unterscheiden. Abb. 1 zeigt die die reine Stimmung in blau – d.h. die zehn resonantesten Intervalle, plus die beiden Füller Cis und Fis – und darunter die zwölf Intervalle der gleichstufig temperierten Stimmung in rot.

Abb 1: reine (blau) und gleichmässig temperierte Stimmung (rot), bei Grundton C (logarithmischer Darstellung)

Offensichtlich weichen die Frequenzverhältnisse der temperierten Stimmung von derjenigen der reinen Stimmung ab und entsprechen somit nicht mehr den einfachen Frequenzverhältnissen, welche ursprünglich zu unseren reinen Tonleitern geführt haben. Trotzdem funktioniert die unreine Stimmung und wir hören und unterscheiden kleine und grosse Terzen, Quinten und Sexten, obwohl sie gar nicht mehr rein sind. Sind die temperierten, also unreinen Intervalle dabei weiterhin resonant?

Die Antwort ist ein eindeutiges Ja.

Weshalb die unreine Stimmung trotzdem resonant ist

Abb 2. zeigt die Resonanz, abhängig, von der Frequenzrelation und der Dämpfung. Je grösser die Dämpfung ist, umso kleiner ist die Resonanz, ganz unabhängig von den Frequenzverhältnissen.

Interessant aber ist, wie die Frequenzverhältnisse – in Abb. 2 auf der Horizontalen von 0.0 bis 3.0 eingezeichnet – auf die Resonanzentstehung wirken. Am stärksten ist die Resonanz bei 1.0, also dann, wenn die beiden Medien, das anregende und das angeregte, die identische Frequenz haben. Doch auch wenn das Frequenzverhältnis nicht genau 1 ist, entsteht Resonanz. Dies ist der Grund, weshalb wir auch die temperierte Stimmung als resonant erleben.

Abb. 2: Resonanz in Abhängigkeit von der Präzision der Frequenzverhältnisse [Quelle: https://de.wikipedia.org/wiki/Resonanz (1.8.2021)] Graphikautor:  https://commons.wikimedia.org/wiki/User:Geek3]

Die temperierte Stimmung mit ihren nicht ganz genauen Brüchen führt, wie in Abb. 2 ersichtlich ist, trotzdem zu Resonanzen zwischen den Intervallen, wenn auch zu etwas schwächeren. Weil wir praktisch nur Musik hören, die auf der temperierten Stimmung basiert, haben wir uns zudem daran gewöhnt. Reine Stimmung kann nur von Stimmen und Instrumenten erklingen, welche die Tonhöhen beliebig ändern können. Auf Tasteninstrumenten geht das nicht. Reine Streicherensembles oder unbegleitete Sänger aber können rein musizieren, und gute Ensembles tun das auch.

Zusätzliche Effekte der temperierten Stimmung

Der Hauptnutzen der Temperierung liegt in einer gewaltigen Erweiterung der kompositorischen Möglichkeiten.

Es gibt aber weitere zusätzliche Effekte: Die leichte «Verstimmung» der Intervalle führt zu Interferenzen (Schwebungen). Die Resonanz kann dabei ab- und anschwellen. Die Reibung von zwei unreinen gestimmten Töne kann einen dritten entstehen lassen, der sich den beiden anderen überlagert. Solche Effekte können auch bewusst bei der reinen Stimmung gesucht werden, indem der Sänger oder Instrumentalist die Tonhöhe leicht verschiebt und damit einen bewussten musikalischen Effekt erreicht, mit dem er spielen kann.

Auf diese Effekte möchte ich aber nicht weiter eingehen. Auch nicht auf die sehr interessanten Effekte, welche Klavierstimmer beachten müssen, wie z.B. das sogenannte Strecken über den Gesamttonverlauf. Das Stimmen z.B. eines Klaviers ist muss nämlich mehrere Ziele gleichzeitig beachten. Auch dabei wirken die die drei Welten gleichzeitig: Die Mathematik der reinen Zahlen, die Physik der realen Klaviersaiten und unser subjektiver Eindruck.

Aus zwei Gründen führe ich diese Überlegungen hier aber nicht weiter. Erstens sind die genannten akustischen Phänomene sehr gut beschreiben und zweitens von Fachleuten, die sich darauf spezialisiert haben und wesentlich mehr darüber wissen als ein Informatiker und Amateurmusiker wie ich. Für mich ist die gleichstufige Temperierung einfach eine geniale und praktische Erfindung, die ich sehr gerne akzeptiere, weil sie die harmonischen Möglichkeiten der Musik deutlich erweitert.

Ich setze deshalb diese Serie mit den Erweiterungen der kompositorischen Möglichkeiten fort, die sich durch die gleichstufige Temperierung ergeben

Die ist ein Beitrag zur Entstehung der Tonleitern.

 

Drei-Welten-Theorie

Wie die temperierte Stimmung entstand

Hinterlassen Sie einen Kommentar

Tonleitern vor der Temperierung

Natürliche Tonleitern

Die Tonleitern der menschlichen Kulturen haben sich über die Jahrtausende auf natürliche Weise, d.h. ganz ohne bewusste mathematische Überlegungen entwickelt. Dass trotzdem sehr viel Mathematik dahinter steckt, hat mit den Resonanzen der Tonleitertöne zum Grundton zu tun. Diese Resonanzen sind für uns attraktiv und Musik, die auf solchen Resonanzen beruht, hat die Fähigkeit, menschliche Gemeinschaften zusammen zu bringen.

Mathematisch kann die Resonanz auf Brüche mit möglichst kleinen ganzen Zahlen zurückgeführt werden und wir konnten rechnerisch ableiten, welche neun Intervalle die deutlichsten Resonanzen aufweisen müssen. Nicht zufällig bestehen alle global verbreiteten Tonleitern – d.h. die Standardpentatoniken, unser Dur und unser Moll, die Kirchentonarten und viele mehr – ausschliesslich aus einer Auswahl von fünf, bzw. sieben aus diesen neun Tönen.

Der Grundton und die Spannung

Ebenfalls in allen Kulturen beobachtbar und für uns gar nicht anders vorstellbar ist die Tatsache, dass alle Tonleitern eine klar definierte Basis, d.h. einen Grundton haben, auf den sich die anderen Töne immer beziehen. Dies ist der Grundton, zu dem jeder Tonleiterton seine Resonanz aufbaut, je stärker sie ist, umso ruhiger wirkt der Ton neben dem Grundton, aber auch innerhalb der Melodie. Andererseits, je höher die Zahlen in den Brüchen, d.h. je schlechter die Resonanz zum Grundton ist, umso schärfer und gespannter erscheint uns der Melodieton. Der schärfste Ton in der Dur-Tonleiter ist die grosse Sept (z.B. H in C-Dur), die einen Halbton unter Oktave liegt. Dieser Ton trägt die stärkste Spannung von allen Tönen in der Durtonleiter, er verlangt nach seiner Auflösung auf die Oktave und führt so die Melodie von Spannung zu Entspannung. Diese Spannung ist nur möglich, weil der Grundton hör- oder unhörbar mitschwingt und die Resonanz zu ihm gespannt ist.

Dies alles aber hat noch nichts mit der Temperierung zu tun und funktioniert in reinem Dur.

Weshalb wurden die Tonleitern temperiert?

Zwei Masstäbe: linear und exponentiell

Temperierung bedeutet, dass die Frequenz der Tonleitertöne leicht verändert, vermindert oder erhöht – d.h. temperiert – wird. Dabei werden die Resonanzen auf den ersten Blick leicht abgeschwächt, trotzdem hat sich in der europäischen Musikkultur die Temperierung als selbstverständlich durchgesetzt.

Um die Temperierung zu verstehen, ist es hilfreich zu erkennen, dass wir Intervalle mit zwei verschiedenen Masstäben messen: ein Masstab ist linear, der andere verhält sich exponentiell. Eine genaue Erklärung der Gründe und Konsequenzen der zwei Masstäbe finden sie hier. Vereinfacht gesagt geht es darum, dass alle Intervalle relativ sind. Wenn ich also eine Tonleiter von C aus aufbaue, sind die Tonleitertöne auf dieses C ausgerichtet, wenn ich einen anderen Grundton wähle, z.B. das D, dann ist das E von C ein anderes als das E von D.

Beispiel für diese Relativität der Masstäbe

In C-Dur ist der Ton E eine grosse Terz über dem Grundton C, die Frequenz des E beträgt 5/4 des Grundtons C. Ein Ton D ist eine grosse Sekunde über dem C und hat somit 9/8 der Frequenz des C. Wenn wir nun dieses D (=9/8) zum Grundton wählen, dann kommt in D-Dur ebenfalls E vor, aber diesmal als grosse Sekunde. Der entscheidende Punkt ist, dass dieses E nicht genau gleich hoch ist wie das E vorher von C-Dur:

Tonalität / Tonart Frequenz bezüglich Tonleitergrundton Frequenz bezüglich
C-Dur		 Funktion des Tons in C-Dur, bzw. D-Dur
C-Dur C = 1 1 Grundton
D = 9/8 9/8 grosse Sekunde
E = 5/4 5/4 grosse Terz
D-Dur D = 1 9/8 Grundton
E = 9/8 9/8 x 9/8 = 81/64 grosse Sekunde

Tabelle 1: Relativität der Frequenzen bezüglich Grundton

In Tabelle 1 sehen Sie, dass das scheinbar gleiche E in den beiden Tonleitern verschiedene Tonhöhen hat:

E in C-Dur = 5/4        = 1.25
E in D-Dur = 81/64 = 1.266

Wenn ich eine Saite auf das E für C-Dur stimme, dann stimmt die Saite nicht ganz mit dem erwarteten E in D-Dur überein. Der Unterschied ist nicht gross, doch messbar und für feine Ohren durchaus hörbar.

Die reine Stimmung funktioniert nur für einen definierten Grundton. 

Sobald der Grundton wechselt, sind alle Tonleitertöne relativ zum neuen Grundton in Resonanz und die Tonhöhen der früheren Tonart stimmen nicht mehr alle ganz. Grund dafür sind wie dargestellt die doppelten Masstäbe für Intervalle, einmal linear (Hörempfindung) und einmal exponentiell (physikalische Frequenzen).

Die drei Welten

Wieder geht es um die drei Welten nach Penrose: Die Hörempfindung findet in der mentalen Welt statt, die Frequenzen sind Teil der physikalischen Welt und die ideale Welt ist diejenige der Mathematik der ganzzahligen Brüche. Alle drei Welten spielen bei der Musik auf höchst interessante Weise zusammen.

Ziel der Temperierung

Bei der Temperierung geht es nun darum, dass der Grundton frei gewechselt werden kann, ohne dass die von früher bekannten resonanten Tonleitern aufgegeben werden müssen. Es handelt sich um einen genial gewählten Kompromiss, der wirklich beide Ziele vereinen kann.

Historische Entwicklung

Die Faszination für resonante Akustik ist typisch für alle menschliche Kulturen. So entstanden die hochresonanten Tonleitern, die Standardpentatoniken und die Durtonleiter, verschiedene Molltonleitern und die in den gregorianischen Chorälen häufig verwendete dorische Tonleiter. Die Musik, die früher mit diesen Tonleitern gespielt wurde, hatte immer eine konstante Tonalität, d.h. einen Grundton, der nicht geändert wird, solange die Melodie erklingt.  Alle Töne der Melodie vergleichen sich mit dem Grundton und die Tatsache, wie stark der Melodie mit dem Grundton in Resonanz steht, zeigt die Spannung an, welche die Melodie beim jeweiligen Ton hat.

Mehrstimmige Instrumente aus früheren Kulturepochen haben zur Unterstützung der Grundtöne oft zusätzliche Saiten (Bordunsaiten) oder Pfeifen (Dudelsack), deren Tonhöhe nicht verändert werden kann, damit genau diese Spannung des Melodietons zum Grundton hervorgehoben wird. Während die Töne der Melodie variieren, erklingt der Grundton (Bordunton) durch das ganze Stück durch und gibt einen soliden Boden.

In Europa jedoch setzten sich in der Renaissance gewisse Neuerungen durch. So begann man den Grundton während des Stücks zu wechseln. Das erlaubt eine grössere Vielfalt in der Musik. Solange die Tonarten miteinander verwandt waren, entstanden nur geringe Frequenzabweichungen, bei wirklich eng verwandten Tonarten betrafen sie auch nur einen Ton. Je weiter die Tonarten aber voneinander entfernt waren, umso schwieriger wurde es. So klang es z.B. sehr unschön, wenn versucht wurde auf einer Orgel, die in C gestimmt war, in Fis-Dur zu spielen. Nun begann in Europa eine Periode der verschiedensten Versuche mit leicht veränderten (=temperierten) Stimmungen, welche die Unvereinbarkeit der Grundtonverschiebung mit der Reinheit der Intervalle in verschiedenen Kompromissen zu überbrücken versuchten. Letztlich durchgesetzt hat sich im Spätbarock die gleichstufige (gleichschwebende) Temperierung, die einen wirklich überzeugenden Kompromiss darstellt und die reiche Entwicklung der Harmonik in Klassik und modernen Jazz erst möglich gemacht hat.

Mehr dazu im nächsten Beitrag

Die ist ein Beitrag zur Entstehung der Tonleitern.

 

Drei-Welten-Theorie

Zwei schlechter resonante Intervalle für die Lücken

Ausgangslage: Zwei Lücken

Im Vorbeitrag haben wir erkannt, dass in der Reihe der bisher gefundenen zehn Tonleitertönen zwei Lücken bestehen. Können wir dort auch resonante Töne finden? Folgendes wissen wir bereits:

  • Wir kennen bereits die zehn «resonantesten» Intervalle in der Oktave.
  • Mit diesen zehn Intervallen können die fünf Standard-Pentatoniken, und unser Dur und Moll gebildet werden. Dort stören die Lücken also nicht, nur in der Anordnung aller zehn potentiellen Tonleitertöne fallen sie auf.
  • Intervalle kommen nicht allein, weder in einem Akkord, noch in einer Melodie. Wenn wir also ein resonantes Intervall haben, können wir darauf ein zweites ansetzen (addieren) und das resultierende Summenintervall berechnen. Oder wir betrachten den Abstand zwischen zwei Intervallen, und rechnen dazu den Abstand zwischen den beiden Intervallen aus, zählen also das eine vom anderen ab (=Subtraktion).
  • Wegen des exponentiellen Verlaufs der Frequenzen und gegen unsere intuitive Erwartung müssen wir für das Aneinanderfügen der Intervallen ihre Frequenzverhältnisse aber nicht addieren, sondern multiplizieren, und für den Abstand dürfen wir nicht abzählen, sondern müssen dividieren.

Weil wir schon alle resonanten Intervalle innerhalb der Oktave gefunden haben, können wir für die beiden Lücken keine hochresonanten Intervalle mehr erwarten. Doch obwohl die Intervalle im Erfolgsfall zwar nicht mehr so resonant sind, was ihre Resonanz zum Grundton betrifft, sie können sie doch direkte und dadurch sehr resonante Bezüge zu anderen Tonleitertönen haben. Das macht sie im musikalischen Verbund je nach Situation ebenfalls resonanzmässig interessant.

Hier meine Versuche, Töne für die Lücken zu füllen. Zur Illustration zeige ich zu Beginn nochmals die Anordnung der zehn bestresonanten Intervalle aus dem Vorbeitrag:

Abb. 1: Anordnung der zehn resonanten Tonleitertöne in einer Oktave (logarithmische Darstellung)

Die kleinen Sekunden

Für die erste Lücke finden wir keine gute Resonanz zum Grundton, rein rechnerisch haben die Brüche dort viel zu hohe Zähler und Nenner. Der gesuchte Ton darf nur ganz wenig höher sein als der Grundton, das Intervall muss also sehr klein sein. Dazu untersuchen wir als Kandidaten die Abstände zwischen zwei Intervallen, die nahe beieinander liegen. Wir finden so:

Oktave – grosse Sept  = 2 : 15/8 = 16/15 = 1.067
Quart – grosse Terz = 4/3 : 5/4 = 16/15 = 1.067
Kleine Sext – Quint = 8/5 : 3/2 = 16/15 = 1.067
Kleine Terz – grosse Sekunde = 6/5 : 9/8 = 48/45 = 16/15 = 1.067
Grosse Terz – kleine Terz = 5/4 : 6/5 = 25/24 = 1.042
Grosse Sept – kleine Sept = 15/8 : 9/5 = 75/72 = 25/24 = 1.042
Grosse Sext – kleine Sext = 5/3 : 8/5 = 25/24 = 1.042
Kleine Sept – grosse Sext = 9/5 : 5/3 = 27/25 = 1.08

Wir finden so mehrere Intervalle, welche die Bedingungen erfüllen und in die erste Lücke passen. Wie Sie sehen, sind die Intervalle sehr klein, d.h. nur wenig grösser als 1. Mit unserer Methode tauchen immer wieder die gleichen Intervalle auf, insgesamt sind es drei, die sich aus je zwei bekannten und resonanten Intervallen herleiten lassen:

  • 16/15 = 1.042
    – grosse Terz – kleine Terz
    – grosse Sext – kleine Sext
    – grosse Sept – kleine Sept
  • 25/24 = 1.067
    – kleine Terz – grosse Sekunde
    – kleine Sext – Quint
    – Quart – grosse Terz
    – Oktave – grosse Sept
  • 27/25 = 1.08
    – kleine Sept – grosse Sext.

Diese drei Intervalle klingen alle recht scharf. Wir nennen sie kleine Sekunden. In reiner Stimmung gibt es mindestens drei davon.

Die Tritoni

Die zweite Lücke findet sich genau in der Mitte der Tonleiter. Wir versuchen nun, mit Kombination von zwei bekannten resonanten Intervallen diese Lücke zu treffen:

Grosse Sept – Quart = 15/8 : 4/3 = 45/32 = 1.406
Kleine Sept – grosse Terz = 9/5 : 5/4 = 36/25 = 1.44
Grosse Sext – kleine Terz = 5/3 : 6/5 = 25/18 = 1.389
Oktave + kleine Terz – grosse Sext = 2 x 6/5 : 5/3 = 12/5 : 5/3 = 36/25 = 1.44

Wieder erhalten wir drei Intervalle, die nahe beieinander sind:

  • 25/18 = 1.389
  • 45/32 = 1.406
  • 36/25 = 1.440

Einfügung der kleinen Sekunden und Tritoni in die Reihe der Tonleitertöne

Unsere bisherigen Berechnungen betreffen die Frequenzverhältnisse. Diese müssen wir, wie im Vorbeitrag erklärt, logarithmisch umwandeln, damit ihre Abstände dem entsprechen, was wir in unserer mentalen Welt wahrnehmen. In logarithmischer Darstellung (auf Basis 2) erhalten wir folgende Verteilung:

Abb. 2: Drei kleine Sekunden («Halbtöne») und drei Tritoni füllen die Lücken von Abb. 1

Wir sehen zwar, dass die Vorschläge die Lücken jeweils gut füllen, doch für jede Lücke haben wir drei Vorschläge! Welcher ist jetzt der beste? Wir könnten für den mit den kleinsten Zahlen in Zähler und Nenner argumentieren oder für den mit der grössten Häufigkeit unter den Varianten oder den mit dem engsten Bezug zu einer bereits bekannten Tonleiter.  Doch wir schieben die Frage mit gutem Grund bis zur Behandlung der temperierten Stimmung auf

Die ist ein Beitrag zur Entstehung der Tonleitern.

 

Drei-Welten-Theorie

Anordnung der Töne innerhalb der Oktave

Die zehn resonantesten Töne innerhalb der Oktave

Wir untersuchen in dieser Textserie die Tonleitern unter dem Aspekt der drei Welten. Alle drei Welten sind mitbeteiligt, wie wir das z.B. gesehen haben bei der Beantwortung der Frage, weshalb die Tonleitern aller Musikkulturen immer genau eine Oktave abdecken. Nur mathematisch oder physikalisch lässt sich das nicht erklären. Unter Hinzunahme der dritten Welt, nämlich unserer mentalen Welt, wird die Bedeutung der Oktave einleuchtend.

Auch die Auswahl der in der Tonleiter verwendeten Töne  wird über das Phänomen der Resonanz von allen drei Welten bestimmt, wie wir in den Vorbeiträgen gesehen haben. Schauen wir jetzt an, wie die zehn resonantesten Töne im Verlauf der Tonleiter-Oktave angeordnet sind. Wir werden dabei sehen, dass es in der Anordnung Lücken gibt, und uns dann überlegen, welche Konsequenzen wir daraus ziehen können.

Hier also nochmals die 10 Töne. (In Tabelle 1 sind zwar 11 aufgeführt, aber der Grundton und die Oktave zählen als ein Ton, da die Oktave sowohl der höchste Ton der aktuellen, als auch gleichzeitig der Grundton der nächsthöheren Oktave ist, in der sich die Tonleiter ja wiederholt).

Tab. 1: Der Grundton und die zehn resonantesten Intervalle in einer Oktave 

In Tabelle 1 finden sich in der mittleren Spalte die Brüche, welche das Verhältnis des Tonleitertons zum Grundton angeben, bei der Quinte z.B. beträgt die Frequenz das 3/2-fache der Grundfrequenz. Ganz rechts habe ich diese Brüche als Dezimalzahlen angegeben, damit man sie besser vergleichen kann. Die Zahlen bewegen sich selbstverständlich zwischen 1 (Grundton) und 2 (Oktave).

Anordnung der zehn Töne

Um zu sehen, wie sich die zehn Töne innerhalb der Oktave verteilen, nehmen wir die Frequenzen der Töne und vergleichen sie mit der Frequenz des Grundtons. Dies Frequenzverhältnisse finden sich in Tabelle 1 in der rechten Spalte. Diese Zahlen habe ich in die Abbildung 1 übertragen und Sie sehen, wie sich die Frequenzverhältnisse linear anordnen.

So sieht die Anordnung der Intervalle von Tabelle 1 aus:

Abb. 1: Frequenzverhältnisse der potentiellen Tonleitertöne (Tab. 1) in linearer Darstellung. Die Intervalle sind hier von C aus gedacht, d.h. C = Grundton.

In Abb. 1 fällt sofort auf, wie unregelmässig die Anordnung ist. Die Verteilung weist vier grössere Lücken auf, nämlich zwischen C-D, F-G, A-B und H-C. Subjektiv wirkt die Verteilung auch nicht masstabsgetreu, z.B. ist der Abstand zwischen dem Grundton und der Quart (C-F) viel kleiner als der zwischen der Quint und der Oktave (G-C). Wir empfinden aber beide Intervalle als die gleichen, nämlich als zwei Quarten, denn auch zwischen G und C ist der Abstand eine Quarte, genau wie zwischen C und F. Trotzdem ist es von G zu C in Abbildung 1 viel weiter als von C zu F. Weshalb entspricht der wahrgenommene Abstand nicht dem wirklichen Frequenzverhältnis? – Die Antwort liegt wieder im exponentiellen Verlauf der Frequenzen (physikalische Welt), der nicht unserer linearen Empfindung (mentale Welt) entspricht. Wir müssen deshalb die Frequenzen logarithmisch notieren und kommen so zu einer Darstellung, die unserer subjektiven Wahrnehmung entspricht:

Abb. 2: Frequenzverhältnisse der Abb. 1 in einer logarithmischen Darstellung.

Wir sehen, dass in Abb. 2 die Abstände unserer subjektiven Empfindung masstabsgetreuer entsprechen. So ist im Gegensatz zu Abb. 1 z.B. zwischen C und F der gleiche Abstand wie zwischen G und C, was wir als zutreffend empfinden, nämlich beidesmal als eine Quarte. Auch die anderen Abstände entsprechen unserer Empfindung.

Weiterhin sieht die Anordnung jedoch unregelmässig aus und es bestehen Lücken. Diese haben sich nun aber ebenfalls verschoben. Die Lücke C-D ist grösser geworden, während H-C kleiner geworden ist. Wirklich auffällig sind die beiden Lücken C-D und F-G. Können wir da etwas tun? Es geht wieder um die mentale Welt. Wir empfinden die Lücken wirklich. Können wir wieder unsere Resonanzüberlegungen zu Hilfe ziehen, um die Lücken zu füllen? Im nächsten Beitrag erkläre ich wie das geht.

Wir können nämlich Intervalle auch kombinieren. Das kombinierte Intervall weist dann auch noch eine gewisse Resonanz auf, diese ist jedoch meist schwächer als bei den beiden Ausgangsintervallen. Deshalb sind diese Intervalle in den Tonleitern etwas weniger beliebt. Mehr in der Fortsetzung.

Die ist ein Beitrag zur Entstehung der Tonleitern.

 

 

Drei-Welten-Theorie

Reine und unreine Stimmung

4 Kommentare

Die zwei auseinanderstrebenden Ideale einer Theorie

Musiktheorie bewegt sich wie jede Theorie zwischen zwei Extremen. Einerseits erlaubt es eine Theorie, ganz verschiedene Beobachtungen zusammenzufassen und auf einfache Art zu erklären – je einfacher umso besser. Andererseits wollen wir die Erklärung aber auch anwenden, und zwar auf möglichst alles, was wir beobachten. Eine Theorie ist also dann gut, wenn sie möglichst einfach ist, andererseits aber auch möglichst alles erklärt.

Diese beiden Extremziele jeder guten Theorie gleichzeitig zu erfüllen ist die Herausforderung.

Typisch ist der Moment, wo bei der Anwendung der Theorie plötzlich eine Beobachtung auftaucht, die mit der Theorie nicht vereinbar ist. Solche Beobachtungen stürzen die Theorie in eine Krise, z.B. als Max Planck unerklärliche Unregelmässigkeiten in der Schwarzkörperstrahlung feststellte und so die Quantentheorie einleitete oder als Kurt Gödel  mit der Beobachtung einer Lücke in der Logik der Mengen (Unvollständigkeitssatz 1931) sowohl die Mengenlehre als auch die klassische Logik in eine schwere Krise stürzte.

Jede Theorie funktioniert solange gut, bis sie an ihre Grenzen kommt. Dann tauchen plötzlich Lücken auf.

Stimmt die reine Stimmung überhaupt?

Nun, die Krise, von der ich hier spreche, ist etwas älter als die von Max Planck und Kurt Gödel ausgelösten. Sie hat auch schon lange eine sehr praktische Lösung gefunden. Es handelte sich um eine Krise in der Musiktheorie, und die gefundene Lösung ist die gleichstufig temperierte Stimmung. Dies ist die Art, wie wir heute Musikinstrumente stimmen, aber es ist keine Selbstverständlichkeit.

Wie kam es dazu? Schon lange war bekannt, dass mathematische Gesetzmässigkeiten hinter den Intervallen stecken, die wir als wohlklingend empfinden. Tonleitern mit diesen durch einfache Brüche definierten Intervallen gelten als rein, auch unser Dur (ionisch) und alle anderen Kirchentonarten sind perfekt rein, sofern die Intervalle entsprechend den einfachen Brüchen gestimmt werden. Dann sind sie «rein».

Das funktioniert aber nur, wenn man in der gleichen Tonalität bleibt, d.h. wenn die Musik nicht den Grundton wechselt, d.h. nicht moduliert. In der Renaissance aber kamen die Komponisten zunehmend in Aufbruchstimmung und begannen zu modulieren, indem sie den Grundton (die Tonalität),  innerhalb des gleichen Musikstücks wechselten. Dabei wurden die Grenzen der reinen (=pythagoräischen) Stimmung evident.

Die Lücke im pythagoreischen Tonsystem

Als ich das erste Mal vom pythagoreischen Komma hörte, war ich sehr überrascht. Unser perfektes Tonsystem sollte eine – wenn auch klitzekleine – Lücke in der mathematisch perfekten Anordnung haben? Das Tonsystem besteht – wie jeder Blick auf eine Klaviertastatur zeigt – aus zwölf Halbtönen. Wenn ich die Halbtöne einen nach dem anderen nach oben gehe, kommt nach sieben Halbtönen die Quint und nach zwölf die Oktave. Wenn ich also zwölf Quinten (=12×7 Halbtöne) hochgehe, bin ich mathematisch gesehen am gleichen Ort, wie wenn ich sieben Oktaven (=7×12) hochgehe, nicht wahr?

Soweit die Mathematik, die mir als Kind sehr eingeleuchtet hat und ich war erstaunt, dass es nicht so sein sollte. In Wirklichkeit kommt man nach zwölf Quinten nämlich zu einem etwas höheren Ton als nach sieben Oktaven. 12×7 ist in diesem Fall nicht 7×12. Dieser Unterschied ist das pythagoreische Komma.

Woher kommt es? Die Ursache liegt – wie so oft – in einem unerwarteten exponentiellen Wachstum. Im Beitrag zum pythagoreischen Komma erkläre ich, wie und weshalb diese Lücke im pythagoreischen Tonsystem entsteht

 

Die ist ein Beitrag zur Entstehung der Tonleitern.

Drei-Welten-Theorie

Wie entsteht das pythagoreische Komma?

Das pythagoreische Komma

Das pythagoreische Komma zeigt, dass unser Tonsystem nicht perfekt stimmt, sondern eine Lücke hat, deren Form und Ursache ich in diesem Beitrag beschreibe.   Das Komma ist sowohl für unsere Musikpraxis relevant, auf die es ganz konkrete Auswirkungen hat, als auch erkenntnistheoretisch, da es typisch ist für die Probleme, die wir beim Zusammenspiel unserer drei Welten (nach Penrose) beobachten. Es ist in diesem Sinn nicht nur für Musiker ein relevantes Thema, sondern auch für philosophisch interessierte Menschen, die sich fragen, wie Mathematik (ideale Welt), Physik (physikalische Welt) und unser Erleben (mentale Welt) zusammenhängen.

Als erstes erkläre ich hier, weshalb es zu diesem Komma kommt.

Intervalle addieren

Was geschieht, wenn wir zwei Intervalle, z.B. eine Quint und eine Quart addieren? Wir werden sehen, dass eine solche Addition in den einen Fällen perfekt funktioniert, in anderen aber zu Problemen führt. Hier liegt der Ursprung des Kommas, aber auch der temperierten Stimmung. Weshalb entstehen hier überhaupt Probleme? Darauf möchte ich jetzt eingehen, auf die Ursachen, später aber auch auf die Lösung des Problems.

Addieren heisst für Intervalle Multiplizieren

Können wir Intervalle einfach so addieren? Das Problem dabei ist, dass wir die Intervalle linear empfinden, die Frequenzen aber nicht linear ansteigen, sondern exponentiell.

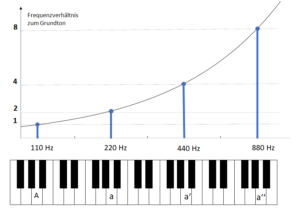
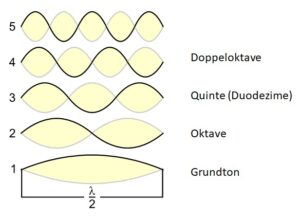
Abb. 1: Exponentieller Anstieg der Frequenzen

Zwischen dem Ton A (110Hz) und dem Ton a (220 Hz) besteht ein Abstand von 110 Hz. Dieser Abstand entspricht einer Oktave – aber nur dort! Wenn wir nun den Abstand von Ton a zu Ton a' messen, was wieder einer Oktave entspricht, bekommen wir aber nicht 110 Hz sondern 220 Hz. Und von a' zu a" sind es bereits 880 Hz. Die Frequenzen verhalten sich eben nicht linear, sondern exponentiell, wie in Abb. 1 dargestellt.

Hier liegt nun die Ursache des Problems, das europäische Musiker dazu geführt hat, verschiedene temperierte Stimmungen auszutesten, wobei sich letztlich die gleichmässig temperierte Stimmung durchgesetzt hat.

Wenn wir Intervalle addieren, müssen wir also ihre Frequenzverhältnisse multiplizieren, wenn wir sie abzählen, müssen wir sie dividieren. Die Operationen verschieben sich von Addition/Subtraktion zu Multiplikation/Division. Diese Art Verschiebung ist den Mathematikern bestens bekannt. Vor den Taschenrechnern und Computern benutzten Techniker sogenannte Logarithmentabellen und Rechenschieber, die auf genau dieser Verschiebung basieren. Ebenso kommt der Effekt bei der kombinatorischen Explosion zu tragen oder beim Verlauf von Epidemien.

Beispiele für Intervall-Additionen

Was uns bei Intervallbetrachtungen immer interessiert, ist das Zahlenverhältnis der Frequenzen der beiden Töne des Intervalls: also der Bruch zwischen der Frequenz des höheren geteilt durch die Frequenz des tieferen Tons: X = f2/f1. Dieser Bruch bestimmt das Intervall, das wir wahrnehmen.

Oktave und Oktave

Siehe Abb. 1: Wir addieren zwei Oktaven, z.B. A-a und a-a'.

Die erste Oktave (A-a) misst 220/110 = 2
Die zweite Oktave (a-a') misst 440/220 = 2
Die beiden Oktaven zusammen ergeben 2×2 = 4

Die Multiplikation ist hier korrekt, denn a' ist 4 mal so schnell wie A (440Hz / 110Hz). Zwei Oktaven führen also zu einer Vervierfachung der Grundfrequenz.

Quinte und Quarte

Die Quinte entspricht einer Frequenzbeschleunigung auf 3/2
Die Quarte einer Beschleunigung auf 4/3

Quinte und Quarte zusammen ergeben 3/2 * 4/3 = 12/6 = 2

2 entspricht einer Oktave. Somit ergeben eine Quinte und Quarte zusammen rechnerisch genau eine Oktave. Auch hier entspricht die Mathematik unseren Hör-Erwartungen.

Weitere Additionen zu einer Oktave

Kleine Terz plus grosse Sext = 6/5 * 5/3 = 30 /15 = 2
Grosse Terz plus kleine Sext = 5/4 * 8/5 = 40 /20 = 2

Über die Oktave hinaus

Zwei Quinten: 3/2 * 3/2 = 9/4 = 2.25

2.25 ist grösser als 2, wir haben also den Bereich der Oktave verlassen. Wo sind wir gelandet? Bei einer None. Eine None ist eine Oktave plus eine grosse Sekunde. Geht das auf? Wir rechnen:

Oktave plus grosse Sekunde = 2 * 9/8 = 18/8 = 9/4 = 2.25
Ja! Es funktioniert. Wenn wir zwei Intervalle addieren, müssen wir ihre Brüche multiplizieren.

Subtraktion wird Division

Es geht natürlich auch umgekehrt, wir können ein Intervall von einem anderen abziehen. Dann müssen wir dividieren:

Eine Oktave weniger eine Quinte = 2 : 3/2 = 4/3 = eine Quart
Eine Quinte weniger eine Quart = 3/2 : 4/3 = 9/8 = eine grosse Sekunde.

Warum funktionieren diese Rechnungen?

Ich war überrascht, zu sehen, dass trotz der Verschiebung der Rechenoperationen die Rechnungen genau die Resultate liefern, die ein Musiker erwartet. Wie kann das sein? Eine Multiplikation ist doch etwas ganz anderes als eine Addition. Weshalb können wir trotzdem so rechnen?

Der Grund liegt darin, dass unzählige musikalische Menschen über viele Jahrtausende ein Tonsystem entwickelt haben, das genau das erlaubt. Dass die Rechnungen so perfekt aufgehen, ist nämlich keine Selbstverständlichkeit und es ist auch nicht immer so, wie wir gleich sehen werden. In den obigen Beispielen aber gehen sie auf und das rührt nur daher, dass wir die Intervalle klug gewählt haben. Sie sind wie in früheren Beiträgen dargestellt, alles andere als zufällig gewählt, sondern nach den Kriterien für resonante Tonleitern. Und dabei haben wir gesehen, dass Intervalle dann resonant sind, wenn sie Brüche mit ganzzahligen Zählern und Nennern darstellen, und dass es für eine gleichzeitige Resonanz von mehreren Intervallen notwendig ist, dass die beiden Zahlen möglichst klein sind und insbesondere bei der Primzahlzerlegung keine Primzahl grösser als 5 enthalten.

Diese restriktiven Bedingungen erlauben es nämlich, dass wir kürzen können, wenn wir die Intervalle miteinander vergleichen. Hohe Zahlen und insbesondere hohe Primzahlen sind fürs Kürzen ungeeignet. Das Kürzen aber kommt uns, wie wir in den oben stehenden Beispielen gesehen haben, enorm entgegen. Nur wenn wir kürzen erhalten wir aus der Kombination von zwei resonanten Intervallen wieder ein resonantes. Und nur so bleiben wir innerhalb unserer resonanten Tonleiter.

Das ist bei der Tonleiter so, aber auch beim «Addieren» von mehreren Intervallen. Nur leider funktioniert es nicht immer.

Es wäre zu schön …

Der Übergang vom linearen zum exponentiellen Wachstum führt nämlich schneller zu Problemen als wir erwarten. Schon einfachste Rechnungen funktionieren nicht:

Grosse Sekunde plus kleine Sept = 9/8 * 9/5 = 81 / 40 = 2.025
Wir erwarten eigentlich nicht 2.025, sondern 2, d.h. eine reine Oktave,

Grosse Terz minus grosse Sekunde = 5/4 : 9/8 = 40/36 = 10/9 = 1.111
Wir erwarten eigentlich eine grosse Sekunde, also 9/8 = 1.125

Eine Quart und eine Quart = 4/3 * 4/3 = 16/9 = 1.777
Wir erwarten eigentlich eine kleine Sept = 9/5 = 1.800

Sie sehen, unsere Erwartung, dass das Rechnen mit den Intervallen aufgeht, wird enttäuscht. Nur ganz wenige Intervallkombinationen erlauben ein «reines» Rechnen, und das auch nur darum, weil wir unser Tonleitersystem so gut gewählt haben. Alle anderen Intervallekombinationen gehen nicht auf. Meist sind die Abweichungen nicht sehr gross, aber trotzdem sind sie deutlich vorhanden. Das Phänomen, dass die Intervallkombinationen nicht aufgehen, ist unter dem Namen pythagoräisches Komma berühmt geworden.

Das pythagoreische Komma

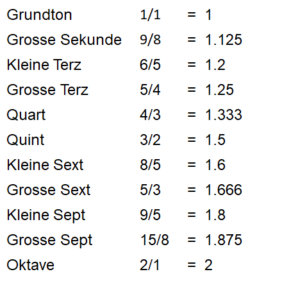
Pythagoras hat bereits gewusst, dass natürliche, d.h. gut klingende Intervalle auf einfache Brüche mit kleinen Zahlen zurückzuführen sind. Die einfachsten Intervalle mit den kleinsten Zahlen in den Brüchen sind bekanntlich die Oktave (2/1), die Quinte (3/2) und die Quart (4/3).

Wie wir oben gesehen haben geben zwei Quinten zusammen eine None. Wie viele Quinten braucht es nun, bis wir wieder beim Grundton sind? Schauen wir das von C aus an und untersuchen wir, wie viele Quinten es braucht, bis wir wieder bei einem C sind:

C – G:  erste Quinte
G – D:  zweite Quinte

Die ganze Reihe ist folgende:
C – G –  D – A – E – H – F# – C# – Ab – Eb – B – F – C

Wir haben somit zwölf Quinten. Das tiefe und das hohe C sind sieben Oktaven voneinander entfernt. Somit ist das obere C über die Quinten gerechnet = 3/212 = 129.746 und über die Oktaven gerechnet = 27 = 128. Die Abweichung zwischen den beiden Berechnungen beträgt: 129.746 : 128 =  1.0136.

Diese kleine Abweichung ist das pythagoreische Komma.

Einordnung des Kommas in den grösseren Zusammenhang

Das pythagoreische Komma ist unausweichlich und rührt letztlich daher, dass wir hier mathematisch unter zwei verschiedenen Flaggen segeln, nämlich derjenigen, die addiert und derjenigen, die multipliziert. Unser Denken, das sich vor allem materiell-räumlich orientiert, ist das lineare Rechnen gewohnt, mit dem Längen gemessen werden. So sehen wir auch die Intervalle. Diese aber funktionieren über die Frequenzen und ihre gegenseitigen Verhältnisse, und diese sind eben nicht linear, sondern exponentiell.

Das ist übrigens nicht der einzige Ort, an dem uns unsere Gewohnheit, linear zu denken, zur Falle wird. Viele Prozesse verlaufen exponentiell, genannt seien hier die kombinatorische Explosion, sobald ein Kollektiv von mehreren Objekten angeschaut wird oder der Verlauf von Epidemien, Gesellschaftstrends etc. Sobald das Geschehen komplex wird, dürfen uns exponentielle Verhältnisse nicht überraschen.

Dies führt uns zum Grundthema dieser Serie zurück, nämlich zum Verhältnis der drei Welten. Was ist die Rolle der Mathematik für die Physik und unseren Geist? Ich lasse diese Frage hier offen und bleibe vorerst auf dem Gebiet der Musik.  Im nächsten Beitrag werde ich erläutern, welche Vorteile unsere Lösung des Komma-Problems, nämlich die gleichmässig temperierte Stimmung bietet.

Fazit

  1. Intervalle werden verrechnet, indem man die Brüche ihrer Frequenzen multipliziert und dividiert.
  2. Dies widerspricht unserer intuitiven Vorstellung, dass dabei addiert und subtrahiert wird.
  3. Aus diesem Grund führen die meisten «Additionen» und «Subtraktionen» von zwei Intervallen nicht zu den erwarteten reinen Intervallen.
  4. Nur ganz wenige Additionen/Subtraktionen von Intervallen führen wieder zu reinen Intervallen. Dies ist nur dann möglich, wenn die Brüche der beteiligten Intervalle ein Kürzen ermöglichen.
  5. Dabei gelten die gleichen Regeln wie für die Bestimmung resonanter Tonleitertöne: Zähler und Nenner müssen kleine Zahlen sein, insbesondere höhere Primzahlen stören Resonanz und Verrechenbarkeit.
  6. Das pythagoreische Komma ist Ausdruck dieser grundlegenden mathematischen Inkompatibilität von Linearität (Addition) und Exponentialität (Multiplikation).
  7. Das pythagoreische Komma setzt somit der reinen Stimmung eine natürliche Schranke.

Wir werden bald sehen, wie das Problems der pythagoräischen Kommas mit der temperierten Stimmung gelöst wird. Doch vorher schauen wir die Anordnung der Töne innerhalb der Oktave in der reinen Stimmung an.

 

Die ist ein Beitrag zur Entstehung der Tonleitern.

Drei-Welten-Theorie, Information

Die Wahrnehmung der Oktave mental

Hinterlassen Sie einen Kommentar

Dies ist ein Beitrag zur Entstehung der Tonleitern und setzt den Beitrag zur Resonanz der Oktave fort.

Die subjektive Seite

Die mathematische oder nach Penrose platonische Welt mit ihren einfachen Zahlenverhältnissen und die physikalische Welt mit ihren Resonanzphänomenen bringt uns die Oktave näher, erklärt aber noch nicht, weshalb dieses Intervall in allen Kulturen die Basis von allen Tonleitern ist. Dazu müssen wir auch die mentale Welt betrachten, das heisst die Welt unserer subjektiven Wahrnehmung.

Diese ist zwar allen zugänglich, doch es bleibt ihre eigene und subjektive Wahrnehmung. Ich kann nicht in Ihren Kopf sehen. Zwar können bildgebende Verfahren (MRI, PET) objektiv feststellen, welche Hirnareale wann aktiv sind, doch was auf diese Weise wahrnehmbar wird, ist der Blutfluss an einer bestimmten Stelle und nicht der Gedanke, wie Sie ihn erleben.

Happy Birthday

Die mentale Welt ist Ihre höchst persönliche Welt, doch für das Primat der Oktave trägt sie einiges bei. Wieder schlage ich ein kleines Experiment vor, zwar kein objektives wie im Vorbeitrag, doch ein durchaus nachvollziehbares. Der Vorteil ist: Mit grosser Wahrscheinlichkeit haben Sie es bereits schon mehrmals durchgeführt.

Es kann auch das Weihnachtslied im Familienkreis sein. Mehrere Menschen singen zusammen und wenn wir Glück haben, singen wir einstimmig. Das ist jedenfalls meistens unsere Absicht. Es funktioniert besser, wenn alle Sänger etwa die gleiche Stimmlage haben. Was aber, wenn Frauen und Männer und Kinder zusammen singen? Auch dann erkennen wir, wenn alle einstimmig zusammen sind. Wir singen zwar nicht die gleichen Frequenzen, sondern Frequenzen mit einer Oktave Abstand, merken das aber praktisch nicht. Der Abstand von einer Oktave klingt für uns als der gleiche Ton. Wenn ich als Bass neben dem Alt die tiefere Oktave nicht treffe, singe ich falsch, wenn ich sie treffe, singe ich richtig. Das ist die subjektive Wirkung der Oktave: Es ist der gleiche Ton.

Die Resonanz in der physikalischen Welt erleichtert dieses subjektive Zusammenfallen der Töne im Oktavabstand, und vermutlich unterstützen uns die Resonanzverhältnisse auf der Basilarmembran des Innenohrs darin, die beiden Frequenzen auch subjektiv in unserer mentalen Welt zusammenzubringen.

Erster und zweiter Oberton

Die Oktave als erster mathematisch-physikalisch möglicher Oberton unterscheidet sich in dieser Beziehung vom zweiten Oberton, der in der Tonleiter auf eine Quint fällt. Zur Verdeutlichung des mathematischen Bezugs zeige ich nochmals die Schwingungsverhältnisse von Grundton und den ersten Obertönen:

Abb. 1: Oktave und Quinte als Obertöne

Weshalb ist nun die Oktave das Merkmal der Einstimmigkeit und nicht die Quinte, obwohl beide mathematisch und physikalisch die engste Beziehung zum Grundton haben? Die Quinte ist zwar mathematisch gesehen etwas weiter weg vom Grundton als die Oktave, aber die Doppeloktave ist es noch weiter und trotzdem empfinden wir die Doppeloktave genau wie die Oktave mental als den «gleichen» Ton wie den Grundton.

In der mentalen Welt, also in unserem Erleben, unterscheiden sich Oktave und Quinte deutlich. In dieser Welt sind die Oktave (und alle Mehrfach-Oktaven) der «gleiche» Ton – die Quinte aber ist ein anderer Ton. Das ist überall auf der Welt so, in allen Kulturen. Weil ein Ton eine Oktave höher als der gleiche Ton empfunden wird, wiederholen sich die Tonleitern eine Oktave höher, und nicht etwa eine Quinte.

Ein Experiment zur Unterscheidung von Oktave und Quinte in der mentalen Welt

Das oben beschriebene Happy-Birthday Experiment kann erweitert werden und so auch den Unterschied zwischen Quinte und Oktave und die besondere Rolle der Oktave zeigen. Sänger können z.B. versuchen, bei der nächsten Geburtstags-Party den Song nicht eine Oktave tiefer (oder höher) zu singen, sondern eine Quinte. Das dürfte ziemlich schwierig für Sie sein, weil Sie eben nicht den «gleichen» Ton singen wie die anderen. Und falls Sie es schaffen, werden die anderen Sie verwundert ansehen, weil Sie eben die Quinte und «nicht den gleichen Ton» singen. Die Oktave ist der «gleiche» Ton, die Quinte ist es nicht.

Über den Zugang zur mentalen Welt

Die mentale Welt lässt sich bekanntlich schwierig beweisen, da sie völlig subjektiv ist. Obwohl jeder mit seinen Gedanken und Empfindungen dauernd in dieser Welt lebt, ist sie objektiver naturwissenschaftlicher Untersuchung nur indirekt zugänglich. Die Inhalte Ihres mentalen Erlebens können Sie anderen Menschen mitteilen, aber ganz sicher können Sie nie sein, dass die anderen sie auch gleich empfinden. Sie können nur hoffen, dass die anderen Ihr Erleben nachvollziehen können. Doch genau dieses subjektive Erleben und Nachvollziehen macht ja die Musik so interessant. Auf eine ganz besondere Weise teilen wir so unsere Subjektivität.

Fazit

Wir sehen, wie sich genau bei der Oktave die mathematische, die physikalische und die mentale Welt treffen. Die einheitliche Bedeutung der Oktave in allen Musikkulturen der Erde ist nur unter Einbezug aller drei Welten verstehbar.

In der Fortsetzung geht es um die weiteren Töne der Tonleitern. Können diese auch so einfach wie die Oktave erklärt werden?

Dies ist ein Beitrag zur Entstehung der Tonleitern

 

Drei-Welten-Theorie, Information

Resonanz und Oktave

2 Kommentare

Dies ist ein Beitrag zur Entstehung der Tonleitern und setzt den Beitrag zur Oktave fort.

Wir erzeugen eine Resonanz

Falls Resonanz für Sie ein abstraktes – oder noch kein erlebtes musikalisches – Phänomen ist, empfehle ich Ihnen folgendes einfaches Experiment: Suchen sie ein Klavier (kein digitales) und auf dem Klavier einen Ton, den Sie gut singen können. Drücken Sie die Taste mit diesem Ton und singen Sie ihn. Das setzt natürlich schon die Resonanz in ihrem Innenohr voraus, sonst würden Sie den Ton nicht treffen. Als nächstes drücken Sie die Klaviertaste, aber so, dass kein Ton erklingt und halten Sie die stumme Taste nach unten gedrückt. So kann die Saite frei schwingen. Jetzt singen Sie den Ton wieder. Wenn Sie die Tonhöhe der Taste erwischt haben, dann erklingt jetzt der Ton im Klavier, ohne dass Sie die Taste erneut anschlagen. Am besten funktioniert das, wenn das Klavier offen ist, und Sie die Saiten sehen können. Aber auch bei geschlossenem Klavierdeckel funktioniert es, Sie müssen eventuell nur ein bisschen lauter singen. Sie können nun verschiedene Töne singen, z.B. eine kleine Melodie und erkennen, dass der Ton im Klavier genau dann erklingt, wenn Ihre Stimme die gleiche Tonhöhe hat wie die Taste.

Falls Sie Mühe haben, den Ton zu treffen, geht es noch einfacher. Drücken Sie auf dem Klavier das Pedal ganz rechts. Jetzt können alle Saiten frei schwingen. Rufen Sie jetzt laut auf das Klavier ein, am besten bei offenem Deckel. Wieder hören Sie, wie die Saiten schwingen, als Echo auf ihre Stimme.

Einfache Resonanz

Die «Fernwirkung» im obigen Experiment ist keine Hexerei, sondern durch Schallwellen vermittelt. Diese treten mit der Saite in Resonanz. Das typische daran ist, dass die Resonanz nicht bei jeder Frequenz auftritt, sondern genau dann, wenn die Schallwelle die Eigenfrequenz der Saite trifft. Eigenfrequenzen sind Eigenschaften von vielen physikalischen Systemen, z.B. kann auch eine Brücke eine Eigenfrequenz haben oder ein Glas, ein Stück Holz oder ein Topf. Saiten- und Blasinstrumente sind dahingehend perfektioniert, dass sie besonders gut klingen, d.h. dass ihre Eigenfrequenzen besonders kräftig und klangvoll sind.

Resonanzen höheren Grades

Wieder schlage ich ein kleines Experiment vor und wieder benötigen Sie ein Klavier, diesmal sollte es gestimmt sein.

Abb 1: Zwei C’s auf dem Klavier im Abstand einer Oktave

Drücken Sie nun die Taste C auf dem Klavier, und zwar die obere (rechte) Taste C. Auf dem Klavier hat es natürlich viele von diesen C’s, nehmen Sie am besten zwei benachbarte C’s in der Mitte der Tastatur, dort ist das Experiment am deutlichsten zu hören. Sie können auch andere Töne als C’s nehmen, das Experiment funktioniert mit allen Tönen, Voraussetzung ist allerdings, dass der Abstand zwischen den beiden Tönen genau eine Oktave ist. Sie erkennen jetzt auch, woher die Oktave ihren Namen hat, das obere C ist acht (lateinisch: octo) Töne vom unteren entfernt (bei der Zählung wird für die musikalischen Intervalle der Ausgangston immer mitgezählt).

Sie haben jetzt die obere (rechte) C-Taste stumm nach unten gedrückt. Schlagen sie jetzt die untere C-Taste kurz und kräftig an. Sie hören jetzt wieder eine «Fernwirkung». Offensichtlich ist die Saite des oberen C’s durch den Anschlag des unteren in Schwingung geraten. Schlagen Sie nun eine Taste gleich links oder rechts neben dem unteren C an. Bei diesen Tasten können Sie das obere C nicht zum Klingen bringen, es entsteht keine Resonanz.

Weshalb genau bei einer Oktave eine Resonanz entsteht

Grundton und Obertöne

Abb. 2:  Mögliche Schwingungen einer Saite
In Abb. 2 sehen Sie fünf mögliche Schwingungsmuster für eine gespannte Seite. Unten (bei 1) schwingt die Saite mit genau einem Bauch in der Mitte. Bei 2 hat es zwei Bäuche, bei 5 fünf. Gelb ist die schwingende Saite gezeichnet, der schwarze Strich zeigt die korrespondierende Schallwelle, d.h. die Schallwelle (Wanderwelle), welche die gleiche Frequenz hat wie die stehende Welle, welche die klingende Saite darstellt. Diese Frequenz hat die Wellenlänge λ, ist also doppelt so lang wie die Saite.

Der Zustand 1 ist nun der Grundzustand, d.h. der Ton, der im oben vorgeschlagenen Experiment erklingt, wenn Sie eine Klaviertaste drücken. Der Zustand 2 ist der nächste erlaubte Zustand der Schwingung. Hier schwingt die Saite mit zwei Bäuchen, bei 3 sind es drei, etc. Alle Zustände also, bei denen die Saite an den Enden, an denen sie befestigt ist, nicht ausschwingt, sind Zustände, die ein ungehindertes Schwingen der Saite erlauben. Somit ist nicht nur der Zustand der einfachen Saitenschwingung möglich, sondern im Prinzip jeder, der einer Wellenlänge entspricht, die ganzzahlig in die Saitenlänge passt. Bei Zustand 2 ist die Wellenlänge halb so lang wie im Grundzustand und die Frequenz somit doppelt so gross (schnell,hoch). Zustand 2 entspricht mit seiner doppelt so grossen Frequenz dem Ton, der eine Oktave höher klingt, Zustand 4 dem Ton, der zwei Oktaven höher klingt.

Weshalb nun klingt das höhere C nun mit, wenn Sie, wie im Experiment oben vorgeschlagen, das tiefere C anschlagen? – Der Grund liegt darin, dass die Saite des tiefen C’s – wie jede Saite – nicht nur in der Grundschwingung (Zustand 1 in Abb. 2) erklingt, sondern mehr oder weniger in allen erlaubten Schwingungen. Diese Schwingungen überlagern sich also. Wenn nun die von der tieferen Saite ausgehenden Schallwellen die Saite des höheren C’s erreichen, dann enthalten sie neben der Grundschwingung immer etwas leiser auch die höheren Schwingungen und somit genau auch die Schwingung der Saite des höheren C’s. Einer Resonanz steht dadurch nichts mehr im Weg.

Sinusschwingung und Obertöne

Die schwarzen Kurve in Abb. 2 sind mathematisch gesehen Sinuskurven. Mit einem technischen Gerät ist es möglich, solche Kurven akustisch zu erzeugen, man spricht dann von einem Sinusschwingung. Mit natürlichen Klangkörpern, also der Klaviersaite, Ihrer Stimme oder überall sonst in der Natur kommen solche reinen Sinusschwingungen nicht vor, sondern die so erzeugten Schallwellen enthalten immer auch die höheren Schwingungen (Stufen 2 ff. in Abb. 2) in komplexen Überlagerungen mit. Man spricht von Obertönen. Die Anteile der einzelnen Obertöne, d.h. wie viel von den Schwingungen der Stufen 2 und folgende jeweils neben dem Grundton in der Mischung des Klangs mitschwingt, ist sehr variabel und wird von den physikalischen Eigenschaften des klangerzeugenden Mediums bestimmt. Diese Mischungen machen den Charakter des Klangs des jeweiligen Instruments aus.

Interpretation der Saitenschwingungen in den drei Welten

Platonisch → Physikalisch (Von einfach zu komplex)

Wir sehen am Beispiel der schwingenden Saite, wie mathematische Gesetzmässigkeiten aus der  platonischen Welt die physikalische Welt bestimmen. In der physikalischen Welt kommen sie aber sehr verschieden an und es entsteht eine grosse Vielfalt: Auf der Saite entstehen gleichzeitig mehrere Schwingungen, neben dem Grundton entstehen immer gleichzeitig viele Obertöne. Jede einzelne dieser Schwingungen kann mathematisch sehr einfach beschrieben werden. Die Mischung jedoch ist äusserst komplex.

Was mathematisch, d.h. in der abstrakten platonischen Welt sehr einfach ist, wird schnell komplex, sobald es in der physikalischen Welt wirkt.

Die unendliche Treppe in Penrose und «Anti-Penrose»-Richtung

Die Trichter in der Skizze von Penrose stellen m.E. nur eine Richtung der Verhältnisse dar. Penrose betont in seiner Darstellung, dass nicht die ganze Mathematik gebraucht wird, um die Physik zu beschreiben und kommt so zu Mengenverhältnissen, wie sie in der Skizze mit den Trichtern dargestellt sind und die wie die ewige Treppe der Logik zu widersprechen scheinen.

Doch meines Erachtens können die Trichter auch in der Gegenrichtung gesehen werden, dann wenn man die Informationsmenge betrachtet. Diese ist in der physikalischen Welt grösser als in der platonischen. Beim Eintreten der Mathematik in die Physik entsteht Neues, nämlich die komplexe Vielfalt der Mischungsverhältnisse. Diese konkrete Vielfalt in der physikalischen Welt stellt eine Information dar, die weit über die Information der ursprünglichen mathematischen Welt hinausgeht. Die Informationsmenge nimmt in Richtung von platonisch zu physikalisch zu. Das stellt mengenmässig eine Gegenbewegung zum Trichter von Penrose dar. Die unendliche Treppe der drei Welten verliert so bei näherem Hinsehen etwas von ihrem Paradoxie-Schrecken.

Platonisch → Mental

Vermutlich haben Sie schon technisch erzeugte Sinusschwingungen gehört. Sie standen am Anfang der elektronischen Musik und hatten damals den Reiz des Neuen und Technischen. Gerade ihre nackte Reinheit war beeindruckend. Allerdings sind diese Töne sind sehr schnell auch sehr langweilig. Die Reinheit und die sterile Banalität dieser technischen Klänge ist verursacht durch das fehlende Mitschwingen der Obertöne. Die reichhaltigen Informationen dieser Zusatzschwingungen nehmen wir als Hörer wahr und sie machen den Reichtum der natürlichen Klänge aus. Ich möchte nicht auf sie verzichten.

In einem Fortsetzungsbeitrag möchte ich erklären, weshalb die Oktave in der mentalen Welt so wichtig ist und was das dazu beiträgt, dass die Tonleitern in allen Kulturen stets die Oktave als Basis haben.

Dies ist ein Beitrag zur Entstehung der Tonleitern

 

Drei-Welten-Theorie, Information

Die Oktave

Hinterlassen Sie einen Kommentar

Eine bemerkenswerte Gemeinsamkeit

Alle Tonleitern, die ich kenne, bewegen sich im Bereich einer Oktave. Auch Tonleitern, die für uns Europäer ungewöhnlich klingen, arabische, indische, japanische und afrikanische bewegen sich innerhalb genau einer Oktave, d.h. ihr tiefster und ihr höchster Ton haben den Abstand von genau einer Oktave, was für eine Tonart das auch ist.

Ich finde das äusserst bemerkenswert. Das ist so, als ob alle Sprachen der Welt, die ja sehr unterschiedliche Wörter haben, für einen bestimmten Begriff das gleiche Wort verwenden würden, und zwar schon immer und ganz unabhängig voneinander. Woher kommt das?

Die Drei-Welten-Theorie kann nun diese ungewöhnliche Gemeinsamkeit der Tonarten aller menschlichen Kulturen plausibel erklären.

Die Oktave platonisch

Wenn Sie eine Saite auf einer Geige zupfen, erhalten Sie einen Ton. Wenn Sie nun den Finger genau in der Mitte der Saite auf das Griffbrett drücken und dann zupfen, erklingt die Saite eine Oktave höher. Das gleiche gilt für Pfeifen. Eine Pfeife, die halb so lang ist wie eine andere, klingt eine Oktave höher. Offensichtlich liegt der Oktave ein Verhältnis 1:2 zugrunde. Das ist die platonische, d.h. mathematische Seite der Oktave. Einfache mathematischen Verhältnisse (= Brüche) spielen auch bei anderen Intervallen eine Rolle, worauf wir noch kommen werden.

Diese mathematischen Verhältnisse der Verhältnisse zwischen den Tönen – das heisst der Intervalle – sind schon lange bekannt und wurden vom Griechen Pythagoras gelehrt, der vor Sokrates und Platon eine einflussreiche Schule in Süditalien begründete.

Abb. 1: Eine schwingende Saite. Oben ist die Saite links und rechts (0 und 1) befestigt, kann dort also nicht schwingen. Je weiter weg von der Befestigung, umso stärker schwingt sie aus, am meisten in der Mitte. Unten ist in der Mitte ein Finger auf die Seite gedrückt, und sie schwingt nun in der halben Länge und eine Oktave höher. (Mit diesen Beschreibungen sind wir aber von der platonischen bereits in die physikalischen Welt eingetreten).

Das einfaches Zahlenverhältnis erklärt die Einzigartigkeit des gemeinsamen Merkmals Oktave über alle menschlichen Kulturen noch nicht. Weshalb spielt das Zahlenverhältnis für die Tonleitern überhaupt eine Rolle?

Zur Erklärung müssen wir die beiden anderen Welten ansehen, nämlich die physikalische, in der Töne erklingen, und die mentale, in der wir sie wahrnehmen.

Die Oktave physikalisch

Töne

Töne sind materielle Schwingungen in einem Trägermedium, z.B. Luft. Ein Ton enthält ist in der Regel eine Überlagerung von mehreren Schwingungen (Grundton plus Obertöne). An dieser Stelle schauen wir aber nur die Grundschwingung an, die die erkennbare Tonhöhe bestimmt.

Diese Grundschwingung ist eine Sinuskurve und die Tonhöhe wird als Frequenz angegeben, z.B. 440 Hz. Diese Frequenz bedeutet, dass die Sinuskurve 440 mal pro Sekunde hin und her schwingt. Das gleiche tut auch die Saite.

Die Saite schwingt an Ort, man spricht von einer stehenden Welle (siehe Abb. 1 oben). Die Schwingung in der Luft hingegen bewegt sich vom Ort fort (Wanderwelle). Durch ihre stationären Schwingung kann die Saite die Luft bewegen und führt so zu einer Schwingung in der Luft, einer Schallwelle. Dabei überträgt die Saite die Eigenschaften ihrer Schwingung, insbesondere deren Frequenz, auf die Schallwelle.

Die Wellenlänge in einer Wanderwelle, also einer Schallwelle, aber auch z.B. einer Welle auf der Wasseroberfläche ist der Abstand der Wellenbäuche (oder Wellenkämme)  voneinander. Bei einer stehenden Welle, also der Saite in Abb. 1 ist die Wellenlänge gleich der (doppelten) Länge der schwingenden Saite.

Wenn nun die Geschwindigkeit der Wanderwelle konstant ist, dann müssen mehr Wellenbäuche hintereinander kommen, je kürzer die Abstände zwischen ihnen sind. Die Abstände zwischen den Wellenkämmen entsprechen der Wellenlänge, die Zahl der Kämme pro Zeit der Frequenz der Welle. Je mehr Kämme an einem Ort durchlaufen, umso kleiner sind ihre Abstände.

Zwischen der Wellenlänge und ihrer Frequenz besteht somit ein umgekehrt proportionales Verhältnis, d.h. je kürzer die Wellenlänge umso höher muss die Frequenz sein. Deshalb schwingt die halb so lange Saite doppelt so schnell. Das ist der physikalische Ursprung der Oktave.

Tonentstehung

Wie kommt nun die Schwingung in die Saite? Dies rührt daher, dass eine gespannte Saite eine Tendenz zu einer Eigenschwingung hat, Die Spannung der Saite führt dazu, dass ein Anstoss, z.B. ein Zupfen der Saite, in ihr eine Bewegung auslöst, die an den beiden Enden der Saite nicht aufhört, sondern wieder zurück gestossen wird. Auf diese Weise bildet sich die stehende Welle aus. Die Wellenlänge, also der Abstand der Wellenbäuche, wird dabei von der Länge der Saite bestimmt. Der Grund dafür ist, dass an den beiden Enden der Saite keine Bewegung mehr möglich ist, da sie ja dort fest fixiert ist. Ausschwingen kann die Welle nur dazuwischen. Die Wellenlänge muss also genau in die Länge der Saite passen.

Die Oktave mental

Das Innenohr

Wir nehmen Töne mit unseren beiden Innenohren wahr. Diese sind äusserst raffiniert gebaute Organe mit einer schneckenförmigen Struktur, weshalb man auch von der Hörschnecke spricht. Die Schallwelle durchwandert von aussen her die flüssigkeitsgefüllte Hörschnecke und erzeugt durch Resonanz eine Schwingung der sogenannten Basilarmembran, welche  die gesamte Schnecke durchzieht. Entlang der Basilarmembran nehmen sogenannte Haarzellen die Schwingungen der Basilarmembran auf und leiten sie als elektrische Signale nach innen ins Hirn. Durch den komplexen und raffinierten Bau der Schnecke, der hier nur kursorisch beschrieben ist, können die akustischen Signale analytisch zerlegt werden, sodass je nach Frequenz unterschiedliche Haarzellen angeregt werden, je höher die Frequenz umso näher am Eingang der Schnecke, je tiefer umso mehr im Innern.

Die Tonwahrnehmung mental

Bis hier hat die Beschreibung der Tonwahrnehmung über das Innenohr noch nichts mit der mentalen Welt zu tun, es handelt sich nur um die anatomischen Voraussetzungen, d.h. den physikalischen Apparat, der die physikalischen Signale (die Schallwellen) gezielt für die eigentliche Wahrnehmung vorbereitet. Diese findet im Gehirn statt und ist ein subjektiver Vorgang.

Subjektive Vorgänge zeichnen sich dadurch aus, dass sie nicht von aussen nachvollzogen werden können. Wie Sie etwas hören und empfinden, weiss ich nicht, das ist ganz Ihre Welt. Allerdings haben wir als Menschen so viele Gemeinsamkeiten, dass ich in davon ausgehen kann, dass Sie vieles ganz ähnlich erleben wie ich. Wir haben die gleiche Anatomie und die gleichen Lebensbedingungen. Weshalb empfinden viele Menschen die gleiche Musik als schön? Wenn wir von der gleichen Musik gerührt werden, sie gleich wie andere als fröhlich, traurig, tröstend, mitreissend usw. empfinden, zeigt das, dass unsere mentalen Welten trotz ihrer Subjektivität stark verbunden sind.

Dabei spielen kulturelle Aspekte – also gelernte Gewohnheiten – eine ganz wichtige Rolle. Auch die Kultur gehört letztlich in die mentale Welt, sie ist der Geist, d.h. die Subjektivität, die wir teilen. Diese Subjektivität, die individuelle wie die kollektive, fusst aber auch auf den physikalischen Voraussetzungen.

Somit sind wir wieder bei unserem Thema: Weshalb haben alle Kulturen der Menschen die Oktave in ihren sonst so verschiedenen Tonleitern?

Der Grund ist physikalisch erklärbar und liegt in der Resonanz.

Die Resonanz

Resonanz ist eine Voraussetzung, dass die Töne im Innenohr überhaupt ankommen. Denn die Basilarmembran im Innenohr übernimmt die Schwingungen der Schallwellen auf eine ganz bestimmte Weise. Nicht alle Frequenzen finden auf der Basilarmembran die gleiche Resonanz. Das Innenohr ist so gebaut, dass die Basilarmembran am Eingang mit hohen Frequenzen in Resonanz gerät und in der Tiefe mit tiefen. So analysiert das Ohr die verschiedenen Tonhöhen. Aber die Resonanz ist noch für viel mehr verantwortlich, u.a. auch dafür, dass in den tausenden unterschiedlichen Tonleitern die Oktave immer vorkommt. Dieser auffällige Beobachtung werden wir im Fortsetzungsbeitag verfolgen.

Dies ist ein Beitrag zur Entstehung der Tonleitern

 

Drei-Welten-Theorie, Information

Tonleitern in der 3-Welten-Theorie

Hinterlassen Sie einen Kommentar

Tonleitern sind Muster

Wenn Sie eine Melodie hören, steht dahinter eine Tonleiter, d.h. ein Angebot von wenigen, ganz bestimmten Tönen, die überhaupt in der Melodie vorkommen können. Diese Töne in einer linearen Folge bilden die Leiter. Die meisten Melodien, die in unserem Kulturkreis zu hören sind, lassen sich auf eine einzige Tonleiter, die ionische oder Dur-Tonleiter zurückführen, die sieben Töne in ganz bestimmten Abständen aufweist.

Tausende von Tonleitern

Es gibt aber Tausende von unterschiedlichen Tonleitern. Vermutlich kennen Sie neben Dur auch Moll und haben vielleicht etwas von der Pentatonik gehört, von Ganztonleitern, von Phrygisch und Lydisch, von indischen Ragas, japanischen und afrikanischen Tonleitern. Alle diese Tonleitern sind verschieden.

Trotzdem haben sie, wie wir sehen werden, einige verblüffende Gemeinsamkeiten. Warum sollten die Menschen überall auf der Welt in allen Kulturen und bei allen Unterschieden sich freiwillig, ausnahmslos und strikt an diese Gemeinsamkeiten halten? Die Gründe dafür lassen sich gut erklären, wenn man nicht nur eine Welt anschaut, sondern das Zusammenspiel aller drei Welten.

In welcher der drei Welten existiert die Tonleitern?

Tonleitern sind Teil unserer Realität, wie immer wir Realität definieren. Es sei denn, wir definieren die Realität als das, was wir Materie nennen. Dann sind die Tonleitern nicht Teil der Materie. Sie prägen sich zwar in der physikalischen Welt aus, z.B. wenn ein Mensch sie singt oder spielt, aber sie haben eine Identität, die unabhängig von der jeweiligen Ausführung ist. Die Tonleiter ist also in diesem Sinn nichtlokal, wie es typischerweise Entitäten in der platonischen Welt sind. Zwischen der Tonleiter und ihrer Ausführung besteht dann das Verhältnis von einem abstrakten, d.h. platonischen Muster zu seiner materiellen Instanz. Es handelt sich immer dabei um ein 1/n – Verhältnis, denn das Muster ist einmalig, doch daraus können beliebig viele Instanzen gewonnen werden.

Als Muster gehört die Tonleiter in die platonische Welt, auch wenn sie sich in die materielle Welt hinein ausprägt. Gerade die Mathematik hat viel mit der Form der Tonleitern zu tun, was leicht zu zeigen ist, doch andererseits müssen Sie gar nichts von dieser Mathematik wissen, um Tonleitern korrekt zu erkennen und oder zu singen. Ihre mentale Welt, in der Sie die Tonleiter erleben, braucht keine Zahlen und Formeln.

Eine Tonleiter existiert somit in allen drei Welten:

Platonische Welt: Hier existiert die Tonleiter als eine Entität, d.h. als eine Einheit und Ganzheit. Hier existiert jede Tonleiter nur einmal.

Physikalische Welt: Hier existiert die Tonleiter als eine beliebige Zahl von Vorkommnissen – wann immer Melodien auf ihrer Basis ertönen.

Mentale Welt: Hier, nämlich in Ihrem Kopf, erkennen Sie die Melodien und Tonleitern.

Selbstverständlich ist jede Welt ganz auf ihre eigene Weise organisiert. Wie spielen nun die drei Welten zusammen? Wir schauen das am Beispiel der Oktave an.

Dies ist ein Beitrag zur Drei-Welten-Theorie.

 

Drei-Welten-Theorie

Die physikalische Welt

Hinterlassen Sie einen Kommentar

Die Welt der Naturwissenschaften

Die physikalische Welt ist das, was die Naturwissenschaften untersuchen, allen voran die Physik. Die Erfolge des naturwissenschaftlichen Programms sind offensichtlich, sowohl bezüglich der Einblicke in das Funktionieren der Welt, also der Theorie, wie auch bezüglich der dadurch ermöglichten Techniken, also der Praxis. Die Naturwissenschaften haben unsere Welt seit Galileo Galilei fundamental verändert.

Objektivität

Der Erfolg wurde dadurch möglich, dass sich die Denker und Forscher in Europa seit der Renaissance nicht mehr auf das beriefen, was von altersher überliefert war, sondern vorurteilsfrei selber forschten und suchten. Während die Mönche in den Klöstern alte Schriften interpretieren und kompilierten (Scholastik), wagten die freien Geister das zu glauben, was sie in der Natur selber sehen konnten – auch wenn es im Widerspruch zu klösterlichen Autoritäten war.

Mit dem Wegfall der alten Autoritäten brauchte es aber eine neue Richtschnur, damit nicht jeder irgendetwas behaupten konnte. Die These eines Forscher sollte unabhängig überprüfbar sein, und nur das sollte fortan als wahr und zutreffend gelten, was von allen zweifelsfrei beobachtbar ist. Das Ideal der Objektivität war geboren.

Messbarkeit

Aber nicht nur objektiv, d.h. von jedermann überprüfbar, sondern auch ganz genau sollte die Welt beschrieben werden können. Das hat zwei Vorteile: a) Eine These ist umso glaubhafter, je präziser ihre Voraussagen sind. Je genauer gemessen werden kann, umso aussagekräftiger werden die Beobachtungen. b) Neben präziseren Erkenntnissen erlauben die genauen Messungen auch den Bau von immer präziseren Apparaten.

Die Welt von aussen

Die Naturwissenschaften konzentrierten sich somit darauf, was von aussen gesehen und gemessen werden kann. Das ist das, was Penrose als die physikalische Welt bezeichnet. Nicht meine Innensicht, meine Empfindung oder mein Glaube ist gefragt, sondern das, was sich zweifelsfrei von aussen beobachten und messen lässt. Das ist die physikalische Welt.

Die physikalische Welt im Zusammenspiel

Man könnte nun die physikalische Welt als die einzig wahre Wirklichkeit ansehen, doch wird unser Weltbild plastischer, wenn wir die beiden anderen Welten hinzunehmen. Wie spielen die drei Welten zusammen? – Es gibt Brücken von einer zur anderen, es gibt Übergänge, und es gibt Wirkungen von einer Welt in die anderen. Wie das funktioniert, lässt sich am Beispiel der Musik ausführen, die an allen drei Welten teilhat.

Dies ist ein Beitrag zur Drei-Welten-Theorie.