Die Dur-Tonleiter

Die Dur-Tonleiter (ionisch) ist in Europa und auch global mit Abstand die weitest verbreitete Tonleiter. Es handelt sich um eine Heptatonik, also um eine Tonleiter mit sieben Tönen. Sie zeichnet sich durch ganz besondere Resonanzverhältnisse aus, die ihre weltweite Wertschätzung gut erklären können.

Unten habe ich die Töne der C-Dur Tonleiter aufgezeichnet, von unten nach oben aufsteigend und jeweils rechts von jedem Ton sein Intervall zum Grundton. Selbstverständlich ist dieses Intervall das, was die Tonleiter ausmacht. Man könnte die Tonleiter auch auf jedem anderen Ton beginnen und nur von den Intervallen (Sekunde, Terz usw.)  sprechen, da es zur Beschreibung der Tonleiter nur auf die Abstände zwischen den Tönen ankommt. Ich verwende hier jedoch die Töne der C-Dur-Tonleiter, einfach weil das anschaulicher ist und Sie das auch leichter am Klavier oder einem anderen Instrument nachvollziehen können.

Das Intervall bezeichnet das Verhältnis der Frequenzen des jeweiligen Tonleitertons zur Frequenz des Grundton. Dieses Intervall liegt bei jeder Tonleiter immer zwischen 1 (Grundton) und 2 (Oktave). Wir geben es in Form eines Bruchs an.

C      2
H      15/8
A      5/3
G      3/2
F      4/3
E      5/4
D      9/8
C      1

Tab. 1: Die C-Dur-Tonleiter

Die Brüche erlauben uns zu erkennen, was das Typische der Dur-Tonleiter ist. Sehr gut lässt sich zeigen, dass das, was wir subjektiv hören (mentale Welt) ganz parallel läuft zu dem läuft, was in der konkreten Materie (physikalische Welt) geschieht und zu dem, was wir mathematisch mit einfachen Brüchen darstellen können (platonische Welt). Erneut stellt heraus, dass die drei Welten (nach Penrose) auf dem Gebiet der Musik perfekt zusammenspielen.

Alle Töne sind resonant zum Grundton

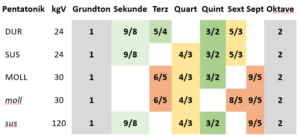
In einem Vorbeitrag habe ich Resonanzkriterien für Tonleitertöne aufgestellt Mit diesen Kriterien erhalten wir 10 Töne, welche jeweils zum Grundton eine starke Resonanz haben. Die Dur-Heptatonik besteht – wie auch die Standard-Pentatoniken – aus einer Auswahl aus diesen zehn am stärksten resonanten Tönen. Somit können wir davon ausgehen, dass die Dur-Tonleiter generell gesehen schon in sich eine starke Resonanz aufweist. Doch nicht jeder Ton ist gleich resonant zum Grundton. Und besonders unter sich sind die Töne sehr unterschiedlich resonant. Hier wird nun die Geschichte interessant. Als erstes schauen wir den Unterschied von der Dur-Heptatonik zur Dur-Pentatonik an.

Die Dur-Heptatonik als Erweiterung der Dur-Pentatonik 

Die Standard-Pentatoniken sind die am stärksten resonanten Tonleitern überhaupt und die resonanteste von ihnen ist die Dur-Pentatonik. Die Dur-Heptatonik kann man als Erweiterung der Dur-Pentatonik sehen. Beide Tonleitern sind Subsets der zehn resonantesten Töne:

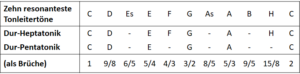
Tabelle 2:Vergleich der Dur-Pentatonik mit der Dur-Heptatonik

Die Töne, die die Heptatonik im Vergleich zur Pentatonik neu aufnimmt, erklären den Unterschied. Während die Pentatonik durchgehend resonant ist und alle Töne beliebig gemischt werden können ohne dass Spannungen auftreten, ist das bei der Heptatonik nicht mehr so. Die beiden Töne, die neu dazukommen, das F und das H, bringen die notwendige Spannung hinein, damit die Sache interessant wird.

Als erstes fällt auf, dass mit dem H der Ton dazukommt, der unter den zehn resonantesten Tönen derjenige mit den höchsten Zahlen in Zähler und Nenner ist. Somit ist er von allen zehn resonanten der Ton mit der schlechtesten Resonanz zum Grundton, also der spannungsgeladenste. Dies betrifft das Verhältnis zum Grundton.

Doch auch das Verhältnis der Tonleiter-Töne untereinander spielt in der Tonleiter eine wichtige Rolle. Wir rechnen es aus, indem wir das Frequenzverhältnis des oberen Tons durch dasjenige des unteren teilen (Grund dafür siehe in der Appendix). Die beiden neu in die Heptatonik aufgenommenen Töne, nämlich das F und das H erzeugen nun rechnerisch und hörbar eine Spannung, wie sie in der Pentatonik bisher nicht vorkommt. Wenn wir z.B. das F zusammen mit dem E erklingen lassen, dann ergibt das ein Frequenzverhältnis von 4/3 : 5/4 = 16/15, ein Bruch, der auf eine schwer zu erreichende Resonanz hinweist. Ähnlich ergeht es dem H neben dem oberen C, hier ist das Verhältnis 2 : 15/8 = 16/8 : 15/8  = 16/15. Zwischen dem H und dem C besteht somit das gleiche spannungsgeladene Intervall wie zwischen dem E und dem F. Das Intervall zwischen dem F und dem H ist nochmals heikler, hier ist der Bruch 15/8 : 4/3 = 45/32.

Spannung und Entspannung

Schlechte Resonanz bedeutet Spannung, da die beiden Töne sich nicht so leicht verbinden. Das empfinden wir subjektiv (mentale Welt), wie Sie leicht testen können, indem sie auf einem Klavier gleichzeitig ein E und ein F anschlagen und das Resultat vergleichen mit dem gleichzeitigen Erklingen z.B. von E und G. Das E und das F reiben sich mehr. Die Mathematik der Frequenzverhältnisse wirkt sich physikalisch als kleinere oder grössere Bereitschaft aus, eine Resonanz einzugehen und das hören wir.

Musikalisch ist die Spannung aber nicht uninteressant. Die Dur-Pentatonik ohne F und H erscheint uns zwar ruhig und harmonisch, aber auch ein bisschen langweilig. Die Dur-Heptatonik hingegen enthält kleine Pfefferkörner, welche eine spannende Schärfe hineinbringen, ähnlich wie Peperoncini in den Speisen. Die Schärfe spüren Sie im Mund aber noch lange nach, während in der Musik die Schärfe ganz präzis ein- und ausgeschaltet werden kann, einfach in dem Sie den spannungsreichen Ton durch eine ruhigen, d.h. problemlos resonanten austauschen. Dieses Spiel von Spannung und Entspannung wird in der Musik ausgiebig benützt.

Die Dur-Heptatonik als Subset der zehn resonantesten Töne

Wie in Tabelle 2 dargestellt, ist die Durtonleiter eine Auswahl von sieben Tönen aus der Liste der zehn resonantesten Töne. Diese Auswahl hat es in sich. Ich werde gleich auf die mathematischen Gegebenheiten eingehen, die sich aus ihr ergeben. Vermutlich werden Sie nicht überrascht sein, dass diese mathematischen Gegebenheiten erneut mit unserem Hörerleben parallel gehen. Schauen wir zuerst, welche Töne im Dur fehlen, es sind dies Es, As und B. Wie immer schauen wir die Brüche dieser drei Intervalle an: 6/5, 8/5 und 9/5. Sofort fällt uns auf, dass alle diese Brüche den Nenner 5 haben. Die Töne der Dur-Heptatonik hingegen kennen keinen Nenner 5.

Nenner wegkürzen

Diese Tatsache des fehlenden Nenners 5 erleichtert die Resonanzen innerhalb der Tonleiter. Wenn zwei Töne den gleichen Nenner haben, kürzt sich dieser weg, wenn wir beide Töne gleichzeitig erklingen lassen. Das Intervall der beiden Töne bekommt so schneller eine Resonanz. Wenn hingegen verschiedene Nenner vorhanden sind, wird die Resonanz erschwert. Aber auch unterschiedliche Nenner lassen sich kürzen, wenn sich die beiden Zahlen durcheinander teilen lassen.

Dazu führen wir eine Primzahlzerlegung durch und erkennen z.B, dass in der Dur-Tonleiter die grosse Sept und die grosse Terz untereinander perfekt resonant sind: Wir vergleichen (teilen) die grosse Sept durch die grosse Terz und erhalten: 15/8 : 5/4 = 3/2, also ein perfekt resonantes Intervall, nämlich die Quinte.

Dies ist möglich weil der Nenner 8 und der Nenner 4 bei der Primzahlzerlegung beide zweimal die Primzahl 2 enthalten (8=2x2x2 und 4=2×2). Somit kürzt sich die 2 zweimal weg. Ähnliches geschieht wo immer möglich auch bei den beiden Zählern.

Aus diesem Grund ist es «klug» von der Dur-Tonleiter, dass sie gerade auf alle Töne mit dem Nenner 5 verzichtet. So stört die 5 nie, und Kürzungen sind besser möglich. Und gekürzte Brüche in den Frequenzverhältnissen bedeuten physikalisch und mental eine bessere Resonanz.

Resonanz der Gesamtheit aller Tonleitertöne

Wir können das Kürzungsverhalten der Gesamtheit aller Töne in einer Tonleiter grob abzuschätzen, indem wir das kgV (kleinste gemeinsame Vielfache) aller Nenner ausrechnen, so wie wir das bereits bei den Pentatoniken getan haben. Die Töne der Dur-Heptatonik weisen nun ein fast unschlagbar tiefes kgV von 24 aus, es ist sogar genau das gleiche wie bei der Dur-Pentatonik mit zwei Tönen weniger.

Dieses kleine kgV rührt natürlich ebenfalls daher, dass wir keine Töne mit Nenner 5 aufgenommen haben, sonst müssten wir das kgV mit 5 vervielfachen und kämen auf 120.

Das kgV ist nützlich,  sagt aber nicht alles

Das kgV zeigt aber nicht das ganze Resonanzverhalten der Tonleiter. Es ist nur ein Mass für die Resonanz aller Tonleitertöne zum Grundton, sagt aber nichts aus zu den Resonanzen der Tonleitertöne untereinander. So kommen wir im Beispiel oben für F und H auf ein Frequenzverhältnis von 45/32, d.h. auch wenn die Töne zum Grundton gut resonant sind, können sie unter sich spannungsgeladen sein.

Das ist aber kein Schwachpunkt, sondern macht die Tonleiter im Gegenteil interessant. Die Dur-Heptatonik ist in dieser Hinsicht eindeutig interessanter als die Dur-Pentatonik, obwohl beide das gleiche kgV haben.

Trotzdem ist das kgV aber ein valabler grober Gradmesser für die grundsätzlichen Resonanz-Möglichkeiten in der Tonleiter, denn bei hohem kgV, d.h. wenn sich die Nenner nicht kürzen lassen, sind die Dissonanzen auf jeden Fall schärfer.

Dreiklänge in der Durtonleiter

Wir wenden nun unsere Resonanz-Überlegungen auf drei gleichzeitig erklingende Töne an.  Analysieren wir z.B. den Dreiklang von C, E und G. Die Frequenzen sind (siehe Tabelle 1): 1 – 5/4 – 3/2. Um das Verhältnis aller drei Töne zueinander zu berechnen, müssen wir alle drei auf gleichen Nenner setzen. Genau dafür brauchen wir wieder das kgV, und dieses ist hier 4. Wir bekommen so aus 1 – 5/4 – 4/2  zu einem Verhältnis von 4/4 – 5/4 – 6/4. Den gemeinsamen Nenner 4 können wir gleich wegkürzen und das Verhältnis der Frequenzen von C-E-G ist somit 4 – 5 – 6.

Dies ist das resonanteste Verhältnis, das in einem Ensemble von drei verschiedenen Tönen überhaupt möglich ist. Beim Dreiklang C-E-G handelt es sich um den einfachen und allen wohlbekannten Dur-Dreiklang. Auf dem Klavier ist er durch die Temperierung etwas gestört, aber auch so können Sie leicht selber austesten, wie eingängig dieser Dreiklang ist. Kein Wunder spielt er in der Pop- und Volksmusik eine derart überragende Rolle.

Drei Dur-Dreiklänge in der Dur-Heptatonik

Die Dir-Heptatonik aber enthält den Dur-Dreiklang aber nicht nur einmal, sondern gleich dreimal. Schauen Sie die Töne F – A – C an, in Brüchen 4/3 – 5/3 – 2, oder alle Töne auf den gemeinsamen Nenner 3 gesetzt: 4/3 – 5/3 – 6/3, also wiederum 4 – 5 – 6. Hier sieht man erneut den Nutzen, den gemeinsame Nenner (hier 3) für die Resonanzen darstellen. Die Dur-Heptatonik hat also gut daran getan, den Ton F hineinzunehmen, der einen zweite Dur-Dreiklang ermöglicht.

Aber auch das H ist gut gewählt, denn zum dritten Mal gibt dadurch den Dur-Dreiklang in der Dur-Heptatonik. Wir starten diesmal mit dem G und nehmen das H hinzu. Als drittes nehmen wir das D, dieses eine Oktave höher als gewohnt, also gleich über dem höheren C. Dazu müssen wir (siehe Rechenregeln) das 9/8 des D mit 2 multiplizieren und bekommen 9/4. Dieser Bruch ist grösser als 2, liegt also bereits über der Oktave. Schauen wir jetzt die Töne G – H – D an, die Frequenzen sind: 3/2 – 15/8 – 9/4. Mit dem kgV=8 bekommen wir: 12/8 – 15/8 – 18/8. Wir können nun Zähler und Nenner kürzen und erhalten wieder 4 – 5 – 6, also das gleiche Verhältnis wie oben, d.h. den gleichen perfekt resonanten Dur-Dreiklang wie beginnend mit dem C oder dem F.

Die Dur-Heptatonik enthält somit den Dur-Dreiklang gleich dreimal, denn dreimal lassen sich drei Töne aus der Heptatonik miteinander auf diese höchst resonante Weise verbinden. Bemerkenswert ist aber auch, dass sich die drei Dreiklänge untereinander nicht so gut mischen können. Das ist gut hörbar, die Mathematik entspricht auch hier wieder perfekt dem subjektiven mentalen Erleben (Sorry, ich muss das einfach immer wieder bringen mit den drei Welten, ich bin selber überrascht, wie gut die drei bei den Tonleitern zusammen kommen).

Natürlich wurde die Dur-Tonleiter nicht «erfunden«, schon gar nicht von einem Mathematiker. Die Tonleiter wurde vielmehr gefunden, und zwar von Menschen, die selber aktiv Musik machten und dabei auf die speziell interessanten Resonanzverhältnisse aufmerksam wurden, die sich bei dieser Zusammenstellung von Tönen ergeben.

Es ergeben sich nämlich drei isolierbare Auswahlen von Tönen aus der Dur-Tonleiter, die in sich jeweils gut resonant sind, aber zu den anderen beiden Auswahlen weniger gut harmonieren. Das ergibt drei unterschiedliche Farben oder Harmonien, die in der Tonleiter getrennt abrufbar sind und deren Abfolge in einem Musikstück geplant werden kann und so eine musikalische Geschichte erzählt. Die drei Farben definieren sich durch den jeweiligen Grundton des Dreiklangs, nämlich durch den Tonleiter-Grundton (C), seine Quart (F) und seine Quint (G). Die drei Töne heissen auch Tonika (Grundton), Subdominant (Quart) und Dominante (Quint). Die Möglichkeit, mit solchen Farben zu spielen, geht weit über die Möglichkeiten der Dur-Pentatonik hinaus und wurde in Europa im Verlauf der Jahrhunderte immer mehr perfektioniert.

Moll-Dreiklänge

Auch diese haben ein spezielles Resonanzverhältnis, nämlich 10 – 12 – 15. Die Zahlen sind etwas höher als im Dur-Dreiklang, was den Moll-Dreiklang etwas weniger resonant macht. Doch für drei verschiedene Töne ist das Verhältnis immer noch extrem einfach und somit resonant und Moll-Dreiklänge sind ganz bestimmt keine Dissonanzen.

Beim Moll-Dreiklang kommt mit der Mollterz zum ersten Mal ein Frequenzverhältnis mit Nenner 5 vor, Dur hingegen kennt das nicht und bevorzugt Nenner basierend auf der Primzahl 2. Dadurch ergibt sich eine deutlich andere Farbe. Mit dem Nenner 5 sind wir schon bei der höchsten «erlaubten» Primzahl angelangt, viel höher als mit der 2 und seinen gut teilbaren Vielfachen des Durs. Moll klingt deshalb weicher, spezieller und nicht so strahlend wie Dur.

Die Moll-Dreiklänge finden sich nicht nur in der Moll, sondern auch in der Dur-Heptatonik, einfach basierend auf weniger prominenten Tönen der Tonleiter, konkret auf dem D, dem E und dem A, doch grundsätzlich lassen sich auch in der Dur-Tonleiter Mollfarben erzeugen, wenn auch nur auf Nebentönen.

Fazit

Insgesamt bieten die sieben Töne der Dur-Tonleiter eine fast unerschöpfliche Quelle an Kombinationen. Die Dur-Tonleiter vereinigt ein maximales Mass an Resonanz mit der Möglichkeit, Spannung und verschiedene Farben zu erzeugen. Dies alles lässt sich mit einfachem Bruchrechnen mathematisch einfach nachvollziehen – in vollem Einklang mit dem, was wir subjektiv hören.

Als nächstes werfen wir einen Blick auf den Unterschied zwischen reiner und unreiner Stimmung. Interessanterweise ist es ja gerade die unreine Stimmung, welche die aktuelle Musikkultur prägt, und nicht etwa die reine. Die unreine Stimmung hat gewichtige Vorteile gegenüber der reinen und sie wurde in Europa bewusst gesucht.

Dieses ist besonders interessant, weil es zeigt, wie die reine mathematische Welt in der physikalischen an Grenzen kommt. Diese Tatsache hat zur gleichmässig temperierten Stimmung geführt, einer «unreinen» Stimmung, die aber heute für uns die gewohnte ist – und das aus guten Gründen. Lesen sie deshalb im nächsten Beitrag, wie es dazu gekommen ist.

Die ist ein Beitrag zur Entstehung der Tonleitern.

Wie wir im Vorbeitrag gesehen haben, bilden die Töne C – D – E – G – A – C die Standard-Dur-Pentatonik.

Insgesamt lassen sich mit den einfachen Kriterien für resonante Tonleitern noch vier weitere Pentatoniken bilden. Diese fünf Pentatoniken sind die fünf Tonleitern, welche nach unseren mathematischen Kriterien unter allen Tonleitern am leichtesten Resonanzen unter allen ihren Tönen erlauben.

Wir werden später sehen, dass wir mit unserem Pool der neun am stärksten resonanten Töne alle traditionell in Europa gebräuchlichen Tonleitern bilden können. Bei den Heptatoniken, z.B unserem diatonischen Dur, sind jedoch gewisse Töne miteinander schlecht resonant, was musikalisch eigentlich interessanter ist, da dadurch eine natürliche Struktur innerhalb der Tonleitertöne entsteht.

Die Pentatoniken hingegen haben keine «falschen» Töne, wie immer man sie mischt. Es gibt bildlich gesprochen keinen Widerstand, welche Töne man auch zusammen erklingen lässt.

Die fünf Pentatoniken sind:
(auf Basis C)

C –  D  –  E  –  G  –  A  –  C

C –  D  –  F –  G  –  A  –   C

C – Eb – F –  G   – Bb  – C

C – Eb – F –  Ab – Bb  – C

C – D  –  F –  G   – Bb  – C

Die gleichen Töne in Brüchen:
(Grundton = 1)

1 – 9/8 – 5/4 – 3/2 – 5/3 – 2

1 – 9/8 – 4/3 – 3/2 – 5/3 – 2

1 – 6/5 – 4/3 – 3/2 – 9/5 – 2

1 – 6/5 – 4/3 – 8/5 – 9/5 – 2

1 – 9/8 – 4/3 – 3/2 – 9/5 – 2

Für die Kalkulation nehme ich an, dass alle Töne gleichzeitig und innerhalb einer Oktave erklingen, mit dem jeweiligen Grundton als tiefsten Ton. Ich berechne also die Intervalle von jedem Ton zum Grundton. Dann schaue ich die Nenner aller Intervalle an und suche das kleinste gemeinsame Vielfache (kgV) dieser Nenner. Dieses zeigt an, wie leicht zwischen allen Tönen Resonanzen entstehen können:

Tabelle 1: Schwingungsverhältnisse von 5 Standard-Pentatoniken

Wie ist Tabelle 1 zu lesen? 

Ich habe in den verschiedenen Pentatoniken gleiche Intervalle in die gleiche Spalte gegeben. Das führt zu den Löchern in der Tabelle. So hat die Dur-Pentatonik keine Quart und keine Sept. Des Weiteren habe ich Tönen mit dem gleichen Nenner im Bruch die gleiche Farbe gegeben.

Was zeigen die Farben? – Gleiche Nenner bedeuten bekanntlich, dass die beiden Töne besonders resonant sind, weil bei der Berechnung ihres Frequenzverhältnisses die beiden Nenner sich beim Zusammenklingen  sich «wegkürzen». Das führt zu besonders einfachen, d.h. besonders resonanten Verhältnissen zwischen den Tönen gleichen Nenners. Für Sekunden, grosse Terzen und Quinten habe ich drei verschiedene Grüntöne gegeben. Die Nenner sind nicht gleich, basieren aber immer auf der Primzahl 2, sodass mindestens ein Kürzen mit zwei immer möglich ist. Die verschiedenen Grün mischen sich deshalb immer sehr gut.

Mathematisch gesehen: Mit 8 hat die grosse Sekunde den grössten Nenner aller Intervalle im Pool. Doch das ist kein Problem. 8 ist keine Primzahl, sondern 2³, genauso wie der Nenner der grosse Terz 4= 2² ist. Wenn wir nun die Quint zusammen mit der grossen Sekunde erklingen lassen, ist das Verhältnis der beiden Töne 3/2 : 9/8 = 3×8 / 2×9 = 4/3, also eine Quart. Die Quart ist das drittresonanteste Intervall, das innerhalb einer Oktave möglich ist, eine grosse Sekunde und eine Quint sind deshalb perfekt resonant. Das Kürzen erweist sich als wirksam.

Weiter zeigen die Farben in Tabelle 1 auch die verschiedenen Formen von Terz und Sext an. So ist die 5/4-Terz die Durterz und die 6/5 Terz die Mollterz.

Bei den Tonleitern geht es um das Intervall des Melodietones zum Grundton, aber auch um das Verhältnis der Melodietöne untereinander. Das kgV ist ein Indikator dafür, wie naheliegend hier Resonanzen sind. Je tiefer das kgV, umso resonanter ist die Gesamttonleiter. Allerdings kann man auch heikle Töne auslassen, bzw. als speziellen Akzent in einer Melodie einsetzen. Bei den Standard-Pentatoniken mit ihren tiefen kgVs ist das zwar kaum möglich.

Wie unterscheiden sich die fünf Pentatoniken?

Dur und Moll

In der sogenannten Funktionsharmonik, einer speziellen, relativ späten, aber bahnbrechenden europäischen Erfindung, spielt die Terz eine wichtige Rolle. Ob Dur oder Moll steht als Frage immer im Raum. Wir gehen an dieser Stelle (noch) nicht auf die Funktionsharmonik ein, können aber unsere fünf Pentatoniken auch unter diesem Terz-Aspekt ansehen. Dabei sehen wir, dass wir eine Dur-Pentatonik (mit Dur-Terz) und zwei Moll-Pentatoniken (mit Moll-Terz) haben.

Die beiden Moll-Pentatoniken unterscheiden sich darin, dass eine keine Quint hat. Obwohl bei beiden das kgV gleich und tief ist, ist das Fehlen der Quint musikalisch (und resonanzmässig) ein grosses Handicap, weshalb die Mollpentatonik ohne Quint kaum gebräuchlich ist. Unsere übliche Moll-Pentatonik ist diejenige mit der Quint.

Wenn Sie Tabelle 1 ansehen, sehen Sie sofort, den Farbunterschied: Die Moll-Pentatonik hat rötlich gefärbte Töne (Nenner 5), die Dur-Pentatonik hingegen nicht. Die jeweilige Terz zieht weitere Intervalle mit dem gleichen Nenner quasi an. Das ist resonanzmässig begründet. Gleiche Nenner sind Garanten für eine starke Resonanz.

Sus

Das Wort «Sus» kommt von «suspended forth», deutsch «hängende Quarte». Woher kommt der Ausdruck? – In der klassischen europäischen Musik, d.h. in der Funktionsharmonik, ist die Terz entscheidend. Ein Akkord, der keine Terz, dafür die Quart enthält, ist «hängend», das heisst, er muss erst noch aufgelöst werden, die Quart wird als Halbton-Vorhalt gesehen und muss sich zur grossen Terz auflösen. In anderen Stilen, im Jazz, aber auch in der moderneren Pop-Musik, ist ein Sus-Akkord ein Akkord wie jeder andere, eine Farbe wie Moll oder Dur. Auch Sus-Tonleitern gibt es, in der Weltmusik wie auch im Jazz. Die Quart (4/3) ist nach Oktave und Quint das am stärksten resonante Intervall.

Wieder gibt es zwei Formen von Sus-Pentatoniken. Das hohe kgV von 120 der einen Pentatonik rührt daher, dass sie sowohl eine Sekunde (Nenner = 9) wie eine kleine Sept (Nenner = 5) enthält. Hier ist kein Kürzen mehr möglich (wie Sie bei der Berechnung des kgVs selber feststellen können). Die Sus-Pentatonik mit der Sext hingegen hat ein anderes Problem: Quart und Sext bilden mit dem oberen Grundton einen Durakkord (4/3 – 5/3 – 6/3 →4-5-6). Dieser Durakkord auf der Quart ist extrem resonant und wird dadurch so dominant, dass die Tonleiter leicht als Dur-Pentatonik missverstanden werden.

Welche Pentatoniken sind gebräuchlich?

Wegen den oben erwähnten Schwächen der einen Moll und der beiden Sus-Pentatoniken sind eigentlich nur die Dur-Pentatonik und die Moll-Pentatonik mit der Quinte gebräuchlich. Diese beiden Pentatoniken aber sind ubiquitär verbreitet und können ganz leicht gesungen werden. Sie können aber auch auf eine wohlklingende Weise mit anderen Tonleitern/Akkorden verbunden werden, was musikalisch besonders interessant ist. Allein klingen sie etwas banal, in Kombinationen aber zeigen sie ihre ganze Stärke. Für Musiker sind sie perfekte Bausteine.

Zur Fortsetzung schauen wir die Durtonleiter an. Wie resonant ist sie?

Die ist ein Beitrag zur Entstehung der Tonleitern.

Können wir mit den bisher postulierten Kriterien bereits Tonleitern konstruieren, die so attraktiv sind, dass sie real vorkommen? Die Kriterien sehen ja auf den ersten Blick eher künstlich und theoretisch aus – können Sie trotzdem dazu dienen, natürlich gewachsene Tonleitern zu erklären?

In der Tat können sie das. Die mathematischen Kriterien für Resonanz haben offensichtlich in den Ohren der Menschen gewirkt und sie über die Jahrtausende immer wieder Musik erfinden lassen, die als Basisgerüst genau die Tonleitern haben, die wir gleich mit unseren Kriterien mathematisch ableiten können.

Pool von resonanten Tönen

Nur mit unseren Resonanzkriterien haben wir einen ersten Pool konstruiert, der diejenigen Töne enthält, bei denen wir die stärkste Resonanz mit dem Grundton erwarten. Ich zähle diese neun potentiellen Tonleitertöne hier nochmals auf:

Grundton                       1/1   = 1
Grosse Sekund           9/8  = 1.125
Kleine Terz                    6/5   = 1.2
Grosse Terz                  5/4   = 1.25
Quart                               4/3   = 1.333
Quint                               3/2   = 1.5
Kleine Sext                   8/5   = 1. 6
Grosse Sext                  5/3    = 1.666
Kleine Sept                   9/5    = 1.8
Grosse Sept                  15/8 = 1.875
Oktave                            2/1    = 2

Natürlich ist dies nur ein Pool von vielen Tönen und keine sinnvolle Tonleiter. Das Problem ist, dass alle diese Töne zwar einfach und schnell mit dem Grundton in Resonanz eintreten können – doch sind sie auch unter sich resonant?

Zwei Tonleitertöne und Grundton

Es geht also nicht nur um die Resonanz eines Tons mit dem Grundton, sondern zusätzlich um die Resonanz mit weiteren Tönen. Dazu gibt es eine mathematische Grundlage: Wir schauen uns das kgV (kleinstes gemeinsames Vielfaches) der beteiligten Nenner an. Wie das geht, und warum das so ist, ist auf der Seite der Rechengrundlagen für die Resonanzen erklärt.

Das kgV (kleinstes gemeinsames Vielfaches) der Nenner

Die Resonanzkriterien sprechen für eine gute Resonanz, wenn das kgV der beteiligten Nenner möglichst klein ist. Der Grundton hat den Nenner 1, deshalb passt er in jedes kgV, er wird also in jede Kombination gut hinein passen. Wie passen nun die Tonleitertöne zusammen?

Beispiel 1

Quart und Quint: Die Nenner sind 3 und 2, das kgV ist 6, also tief. Auch die Zähler sind tief. Als weiteres Indiz für die Resonanz können wir den Abstand zwischen den beiden Tönen berechnen. Der ist 3/2 : 4/3 = 9/8, also eine grosse Sekunde. 8 ist zwar ein relativ grosser Nenner, was die Resonanz mit anderen Tonleitertönen evtl. stört, doch zur sehr wichtigen Oktave passt sowohl die 8 der Sekunde, wie auch die 2 der Quint sehr gut. Zudem haben beide Töne, Quart und Quint unschlagbar kleine Zähler und Nenner, was sich auf die Mischverhältnisse für weitere Tonleitertöne günstig auswirkt.

Mit anderen Worte: Quart und Quint sind ein perfektes Paar für Resonanz. Mathematisch jedenfalls. Klingt das aber auch gut?

Wie klingt die Kombination subjektiv in unserer Wahrnehmung?

Es geht selbstverständlich nicht nur um Mathematik. Die mentale Welt, unsere subjektive Wahrnehmung entscheidet, ob wir eine bestimme Musik mögen und wie wir sie aufnehmen. Wenn Sie den Grundton mit Quart, Quint und Oktave klingen lassen, können Sie hören, was wir berechnet haben, die Resonanz der vier Töne ist ungetrübt. Die Kombination wirkt sogar eher etwas banal und wir vermissen vielleicht den Pfeffer, den in die Musik, die wir gewohnt sind, die Dissonanzen bringen. Ebenfalls fehlt uns die Süsse der Terzen (Nenner 5 und 6).

Beispiel 2

Wir kombinieren rechnerisch die grosse Sekunde mit der kleinen Terz, also 9/8 mit 6/5: Das kgV ist 40, das Intervall zwischen den beiden Tönen ist 6/5 : 9/8 = 48/45 = 16/15. Mit dem grossen kgV und dem engen Abstand ist dieses Paar in Tonleitern etwas heikler – jedenfalls solange wir das Augenmerk auf eine gute Resonanz legen und alle Schärfen in der Musik vermeiden wollen.

Die gefundenen ersten zwei Tonleitern

Wenn Sie nun Lust haben, können sie selber das kgV und den Abstand zwischen allen oben genannten Tonleitertöne ausrechnen und so einen Pool von Tönen zusammenzustellen, bei dem beides optimiert ist und zwischen allen Tönen möglichst viel Resonanz entstehen kann. Natürlich wollen Sie für die Tonleiter auch mehr Töne als nur gerade drei oder vier auswählen. Wie wär es mit fünf?

Die beiden Tonleitern mit den stärksten Resonanzen, die sich so finden lassen, sind bemerkenswert – es sind nämlich beides sehr bekannte Tonleitern:

1 – 9/8 – 5/4 – 3/2 – 5/3 – 2

1 – 6/5 – 4/3 – 3/2 – 9/5 – 2

Oder mit dem Grundton C:

C – D – E – G – A – C

C – Es – F – G – Bb – C

Pentatoniken

Es handelt sich um zwei Pentatoniken, also um zwei Tonleitern mit fünf Tönen (Das C kommt doppelt, zählt aber nur einmal). Nicht ganz überraschend ist, dass die beiden Tonleitern gute alte Bekannte sind – es handelt sich um nichts anderes als die Dur- und die Mollpentatonik.

Und auch nicht ganz überraschend: Diese beiden Tonleitern kommen global in praktisch allen Kulturen vor, im Regenwald wie in allen Hochkulturen, entweder in Reinform oder dann als das Basisgerüst von anspruchsvolleren Tonleitern.

Theoretische mathematische Überlegungen haben uns dazu geführt, diese beiden Tonleitern zu postulieren, die nicht nur weltweit bekannt, sondern für alle Menschen, kleine Kinder inklusive, schnell verständlich und sehr eingängig sind.

Das ist m.E. kein Zufall. Es sieht so aus, als ob die bisherigen Überlegungen gut mit der beobachteten Realität kompatibel seien.

In der Fortsetzung finden Sie eine Resonanz-Analyse der fünf Standardpentatoniken.

Die ist ein Beitrag zur Entstehung der Tonleitern.